WMR 18 - Support Vector Machines I
Lecture Info
Date:
Course Site: Web Mining e Retrieval (a.a. 2019/20)
Lecturer: Roberto Basili.
Slides: ()
Table of Contents:
1 Linear Classifiers
Dalla teoria della PAC learnability vista nelle precedenti lezione, abbiamo visto come la complessità di un modello può influire negativamente nelle future performance del modello quando questo viene addestrato con dei dati di training non adeguati. Questo ci ha portato a considerare il fatto che molto spesso i classificatori lineari, essendo i più semplici, sono anche quelli che si comportano meglio rispetto a quanto detto prima.
In uno spazio \(n\) dimensionale \(\mathbb{R}^n\), una leggere lineare, ovvero un iperpiano, ha la seguente equazione
\[f(\overline{x}) = \overline{x} \cdot \overline{w} + b \;\;\;\;,\;\;\; \overline{x}, \overline{w} \in \mathbb{R}^n, b \in \mathbb{R}\]
dove \(\overline{x}\) è il vettore dell'istanza da classificare, mentre \(\overline{w}\) è il gradiente dell'iperpiano (o della legge lineare).
La funzione di classificazione è definita a partire dall'iperpiano e ha il compito di separare il piano in due: gli elementi che fanno parte del concetto, e quelli che non fanno parte del concetto che si vuole catturare. Formalmente,
\[h(x) = \text{sign}(f(x))\]
Graficamente,
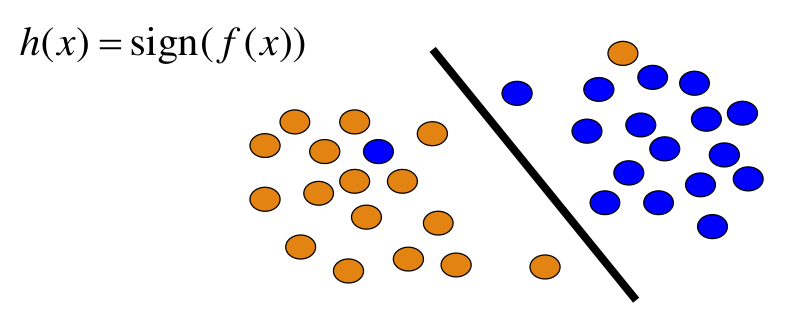
Come è possibile già vedere, i classificatori lineari sono semplici, in quanto hanno pochi parametri e possono essere applicati senza troppi sforzi, ma proprio per questa semplicità potrebbero compiere degli errori e potrebbero non essere completamente consistenti rispetto al training set.
Notiamo che fissato uno spazio di rappresentazione possiamo avere molti iperpiani che dividono lo spazio
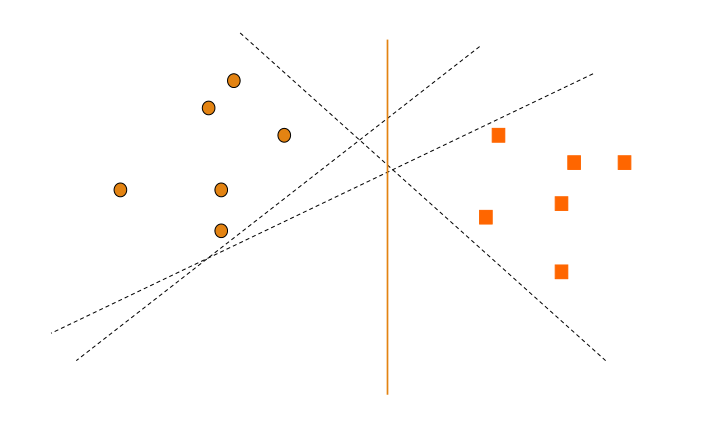
L'idea alla base è quella di scegliere l'iperpiano che minimizza il numero di errori rispetto al training set.
2 Perceprton
A partire dagli anni '50 si cominciò a modellare matematicamente il funzionamento della cognizione umana tramite il modello dei perceprton. Tale modello è graficamente descritto nel seguente modo
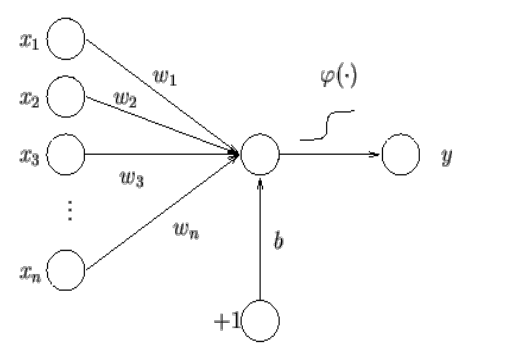
Come possiamo vedere, abbiamo una serie di segnali di input \(x_1, x_2, \ldots, x_n\), ciascuno delle quali è pesato con un peso \(w_i\), che vengono combinati con un valore \(b\) e su cui viene poi applicata una funzione di attivazione \(\phi\), che possiamo pensare essere la funzione segno. Formalmente possiamo avere,
\[\phi(\overline{x}) = \text{sign}\Big(\sum\limits_{i = 1, \ldots, n} w_i \times x_i + b \Big)\]
Questa struttura è stata inspirata dalla struttura tipica dei neuorni
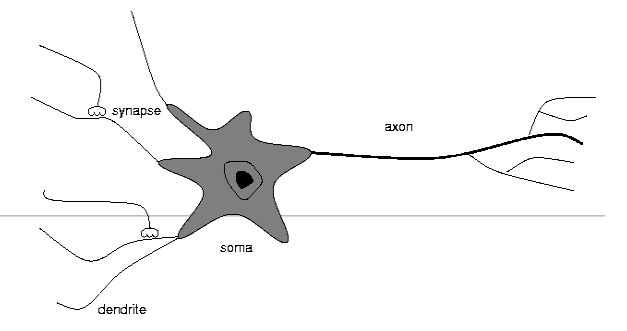
2.1 Functional Margin
Definiamo il margine funzionale (functional margin) dell'esempio \((\overline{x}_i, y_i)\), dove \(y_i = \pm 1\), il valore
\[\gamma_i = y_i (\overline{w} \cdot \overline{x}_i + b)\]
Notiamo che a seconda se il margine funzionale è positivo o negativo allora sappiamo se il punto è stato classificato bene o male. Infatti, \(\gamma_i > 0\) per i punti classificati bene, e \(\gamma_i < 0\) per i punti classificati male.
A partire da un training set \(S\) e fissato un iperpiano possiamo calcolare la distribuzione dei margini funzionali rispetto a tutti i punti del training set. Il margine di un iperpiano \((\overline{w}, b)\) rispetto al training set \(S\) è quindi dato dal margine minimo della distribuzione.
L'idea è quindi quella di trovare l'iperpiano che massimizza il valore assoluto del margine funzionale rispetto a tutti i punti, ovvero di stare al centro.
2.2 Geometric Margin
Ragionando geometricamente troviamo che
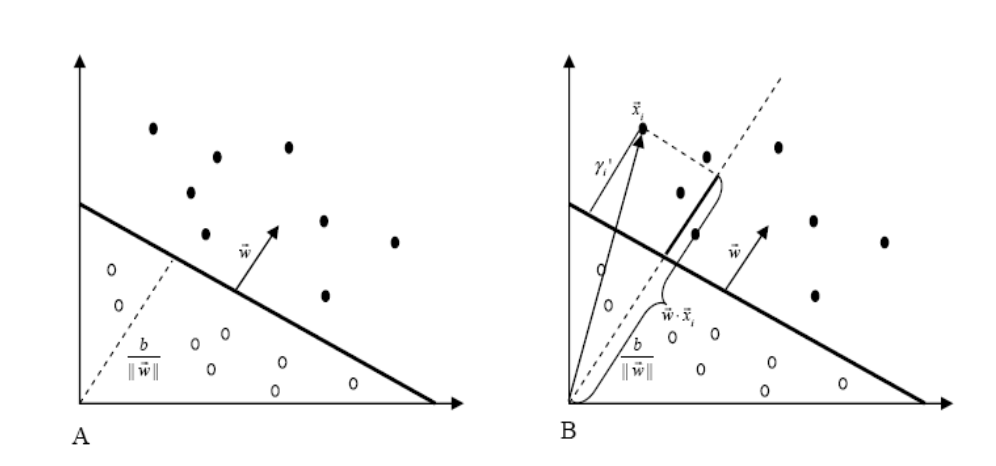
Dove ricordiamo che da
\[\text{cos}(\overline{w}, \overline{w}) = \frac{\overline{x} \cdot \overline{w}}{|| \overline{x} || \cdot || \overline{w} ||}\]
segue che
\[|| \overline{x} || \cdot \text{cos}(\overline{w}, \overline{w}) = \frac{\overline{x} \cdot \overline{w}}{|| \overline{w} ||} = \overline{x} \cdot \frac{\overline{w}}{|| \overline{w} ||}\]
Andando a normalizzare l'equazione dell'iperpiano
\[\Big(\frac{\overline{w}}{|| \overline{w} ||}, \frac{b}{|| \overline{w} ||} \Big)\]
otteniamo il margine geometrico, definito come segue
\[\gamma_i = y_i(\overline{w} \cdot \overline{x}_i + b)\]
Abbiamo quindi che il margine geometrico corrisponde alla distanza dei punti in \(S\) dall'iperpiano. Ad esempio in \(\mathbb{R}^2\) per calcolare la distanza di un punto \(P\) da una retta \(r\) possiamo utilizzare la seguente equazione
\[d(P, r) = \frac{|ax_0 + by_0 + c|}{\sqrt{a^2 + b^2}}\]
Come fatto prima, il margine geometrico di un iperpiano è il più piccolo margine geometrico rispetto a tutti i punti del training set.
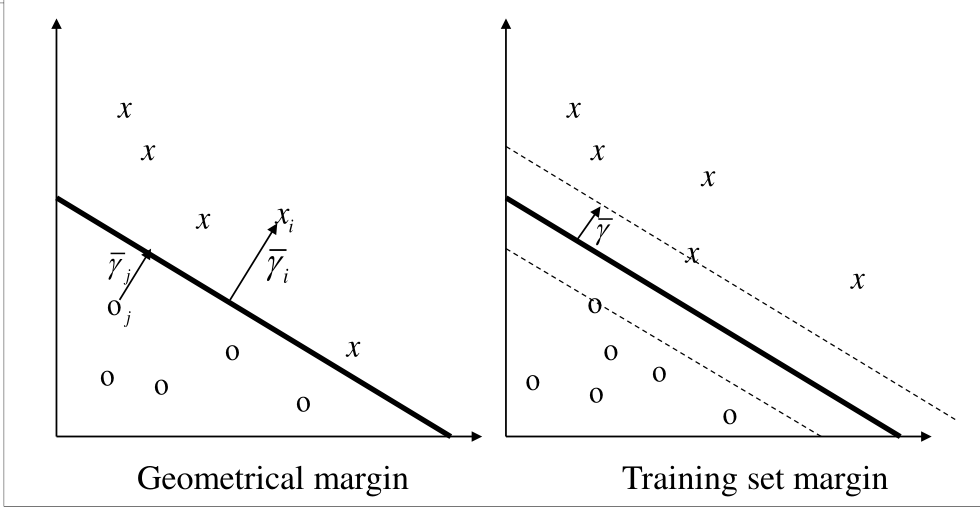
L'iperpiano che corrisponde al massimo margine geometrico è detto maximal margin hyperplane.
2.3 On-Line Algorithm
Il seguente algoritmo viene utilizzato per aggiustare i valori di \(b\) e \(\overline{w}\). È detto on-line in quanto gli aggiornamenti vengono fatti in base a quanto fatto precedentemente.
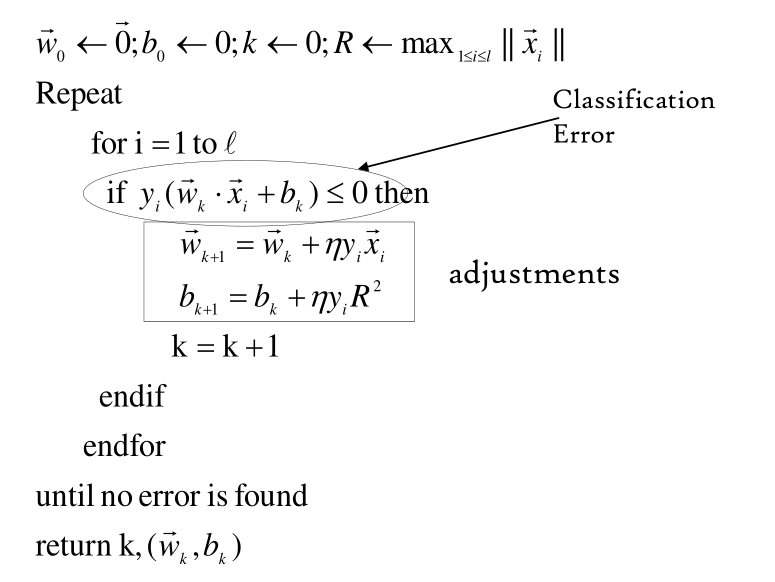
Dove il parametro \(\eta\) è un iper-parametro chiamato learning rate. Più grande è \(\eta\) e più questi cambiamenti saranno aggressivi sui parametri del modello.
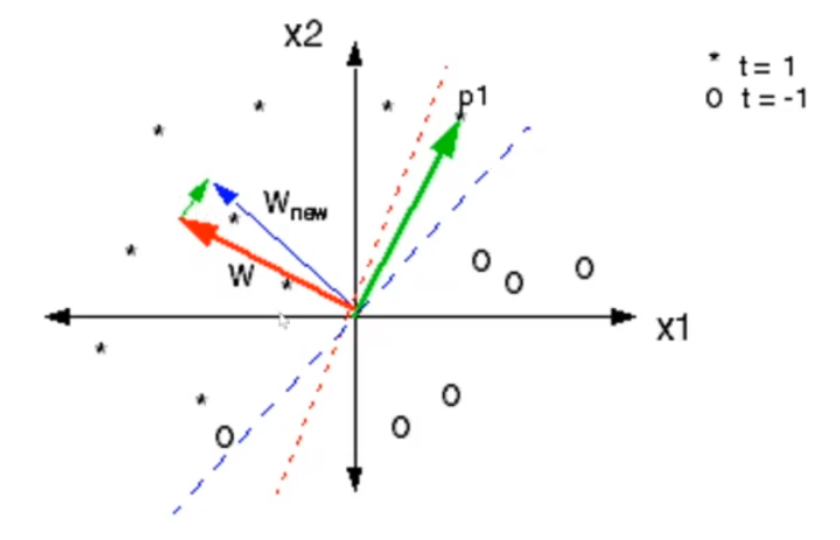
La seguente simulazione è molto utile a capire l'algoritmo di learning appena descritto (Perceptron Learning Algorithm).
Osservazione: La direzione del gradiente mi dice quali sono gli esempi positivi.
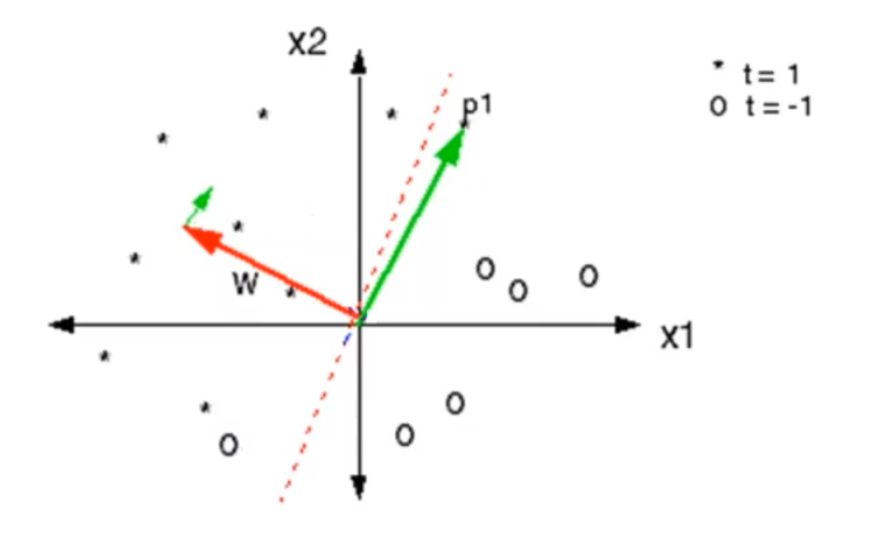
2.4 Novikoff Theorem
Dato un non-trivial training set \(S\), ovvero con \(|S| = m >> 0\), e calcolato
\[R = \underset{1 \leq i \leq l}{\text{max}} || x_i ||\]
Se esiste un vettore \(\overline{w}^*\), con \(||\overline{w}^*||=1\) e tale che
\[y_i (\overline{w}^* \cdot x_i + b^*) \geq \gamma\]
per \(i = 1,\ldots,m\) con \(\gamma > 0\), allora il massimo numero di errori fatti dal percetrone è
\[t^* = \Big( \frac{2R}{\gamma} \Big)^2\]
La conseguenza di questo teorema è che quando abbiamo delle classi linearmente separabili, allora il percetrone è in grado di trovare l'iperpiano di separazione ottimo in un numero finito di passi, che è inversamente proporzionale alla radice del margine.
Il learning rate è molto importante, ma un learning rate troppo grande è da sconsigliare.
2.5 Duality
Andando ad analizzare l'algoritmo mostrato prima possiamo notare che il classificatore lineare ottenuto alla fine può essere visto come il risultato di una combinazione lineare delle istanze del training set. In formula,
\[h(x) = \text{sign}(\overline{w} \cdot \overline{x} + b) = \text{sign}\big(\sum\limits_{j = 1,\ldots,m} \alpha_j y_j \overline{x}_j \overline{x} + b\Big)\]
Notiamo che nella prima formulazione il risultato della classificazione dipende dai parametri dell'iperpiano \(\overline{w}\), mentre nella seconda formulazione il risultato dipende dagli altri esempi del training set. Questi due modi hanno due formulazioni matematiche diverse e fanno riferimento a due spazi diversi:
Il primo spazio è quello dei parametri dell'iperpiano \(\overline{w}\).
Il secondo spazio è quello dei contributi individuali che danno i punti \(x_i\) nel votare la classificazione di \(x\).
3 Limitations of Linear Classifiers
Tra i problemi principali dei classificatori lineari troviamo anche i seguenti:
Problemi quando dobbiamo gestire dati che non sono linearmente separabili.
Trattamento dei noisy data.
I dati devono seguire un formalismo real-value vector, ovvero necessitiamo di un sottostante spazio topologico.
Esistono due approcci per superare il problema della linearità:
Artificual Neural Networks (ANN) approach: L'idea è quella di iniziare dal percetrone e di aumentare il numero di neuorni, organizzandoli in layers complessi. (Approccio architetturale).
Approcci SVMs: L'idea è quella di estendere lo spazio di rappresentazione tramite l'utilizzo di kernel functions. Questo approccio quindi mantiene la linearità ma utilizzando un prodotto scalare in uno spazio più complesso chiamato kernel space. (Approccio topologico).
4 Support Vector Machines
La prima proprietà delle support vector machines è la dualità, che avevamo già menzionato prima
\[f(x) = \text{sign}(\overline{w} \cdot \overline{x} + b) = \text{sign}\Big(\sum\limits_{j = 1,\ldots,m} \alpha_j y_j \overline{x}_j \cdot \overline{x} + b \Big)\]
Notiamo che i dati di input appaiono solamente nei prodotti scalari. Possiamo quindi utilizzare la matrice di Gram, che contiene tutti i prodotti scalari tra ogni coppia di punti in input
\[G = \Big(x_j \cdot x_i \Big)_{i,j = 1}\]
4.1 Maximum Marign Hyperplane
Avevamo già visto che prendendo l'iperpiano che massimizza il margine facevamo la scelta più bilanciata.
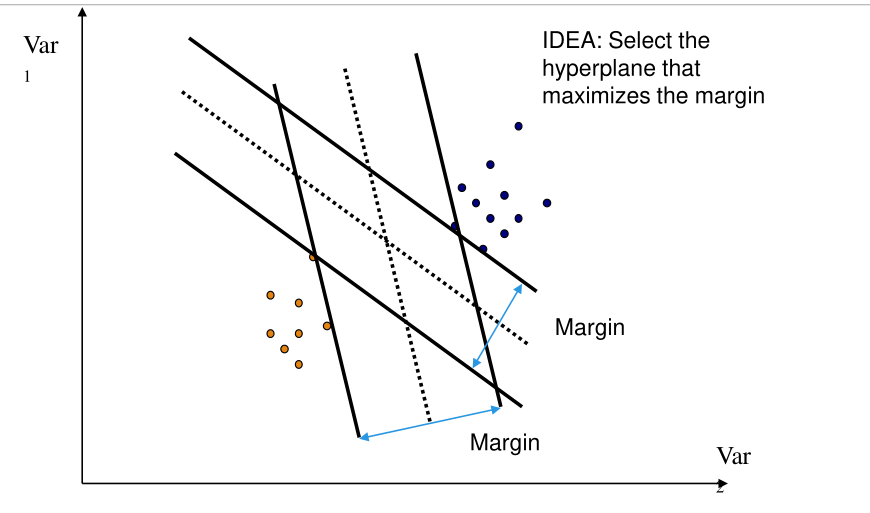
Ogni scelta in particolare ha il proprio margine, che dipende dalla distanza più vicina.
4.2 Support Vectors
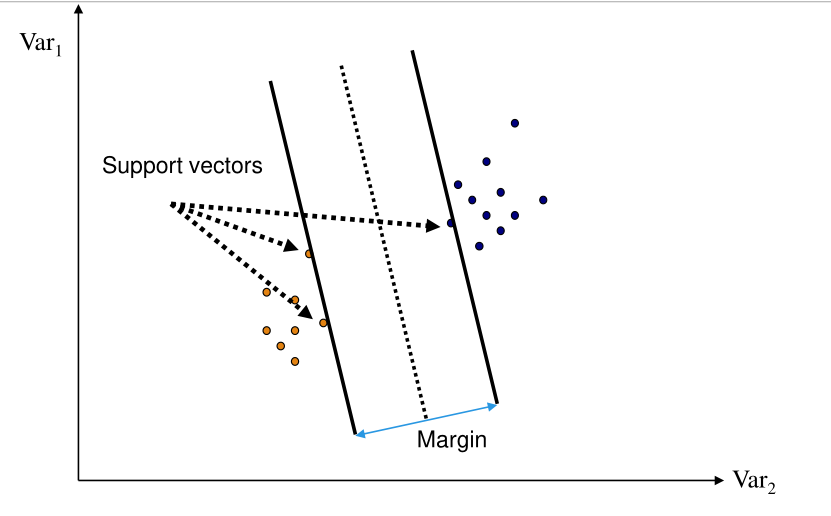
In questo contesto, prendendo l'iperpiano che massimizza il margine, chiamo i support vectors le istanze del training set che sono i responsabili, per le loro posizioni, di determinare l'iperpiano di massimo margine.
4.3 How to Compute the Maximum Margin
Per calcolare questo iperpiano massimo devo trovare l'iperpiano tale che per ogni punto negativo, quando calcolo il valore di \(x\) ottengo un valore che sia al più \(-k\).
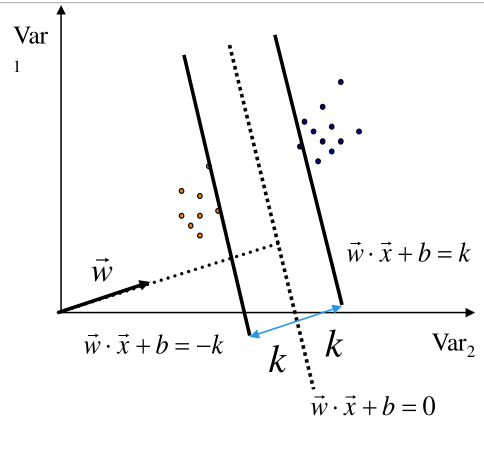
Modellando questi due vincoli in una equazione ottengo che il margine geometrico è pari a
\[\frac{2 |k|}{||w||}\]
Dato che voglio massimizzare tale quantità, rispettando però i vincoli sia per i positivi che per i negativi, ottengo il seguente problema di ottimizzazione
\[\begin{split} &\underset{}{\max} \,\,\, \frac{2 |k|}{||w||} \\ &\text{where } \\ & \;\;\;\; \overline{w} \cdot \overline{x} + b \geq k \,\,\,\,\, \overline{x} \text{ positive ex } \\ & \;\;\;\; \overline{w} \cdot \overline{x} + b \leq -k \,\,\,\,\, \overline{x} \text{ negative ex } \\ \end{split}\]
Riscalando le equazioni e le variabili in modo tale che \(k=1\), ottengo il seguente problema
\[\begin{split} &\underset{}{\max} \,\,\, \frac{2}{||w||} \\ &\text{where } \\ & \;\;\;\; \overline{w} \cdot \overline{x} + b \geq 1 \,\,\,\,\, \overline{x} \text{ positive ex } \\ & \;\;\;\; \overline{w} \cdot \overline{x} + b \leq -1 \,\,\,\,\, \overline{x} \text{ negative ex } \\ \end{split}\]
Infine, faccio un'ulteriore trasformazione al mio problema, ottenendo la seguende versione
\[\begin{split} &\underset{}{\min} \,\,\, \frac12 \cdot ||w||^2 \\ &\text{where } \\ & \;\;\;\; y_i(\overline{w} \cdot \overline{x} + b) \geq 1 \,\,,\,\,\, i = 1,\ldots,l \\ \end{split}\]
Per risolvere il problema l'idea è quella di passare al problema duale utilizzando il lagrangiano.
4.4 The Lagrangian
\[L(\overline{w}, \overline{\alpha}, \overline{\beta}) = f(\overline{w}) - \sum\limits_{i = 1}^m \alpha_i g_i(\overline{w}) - \sum\limits_{i = 1}^l \beta_i h_i(\overline{w})\]
dove,
\(f(\overline{w}) = \tau(\overline{w}) = \frac12 || \overline{w} ||^2\).
\(g_i(\overline{w}) = y_i((\overline{w}\cdot\overline{x}_i) + b) \geq 1\)
Tramite il lagrangiano siamo in grado di fondere assieme i vincoli e la funzione obiettivo nel Lagrangian dual problem
\[\begin{split} &\underset{}{\max} \,\,\, \theta(\overline{\alpha}, \overline{\beta}) \\ &\text{where } \\ & \;\;\;\; \overline{\alpha} \geq \overline{0} \\ \end{split}\]
con
\[\theta(\overline{\alpha}, \overline{\beta}) = \text{inf}_{w \in W} L(\overline{w}, \overline{\alpha}, \overline{\beta})\]