WMR 19 - Support Vector Machines II

• Date: [2020-04-27 lun]

• Course Site: Web Mining e Retrieval (a.a. 2019/20)

• Lecturer: Roberto Basili.

• Slides: ()

• Table of Contents:

---

In questa lezione abbiamo continuato e concluso la trattazione delle Support Vector Machines (SVMs).

Avevamo visto la scorsa lezione che l'approccio SVM segue l'idea ripresa dalla statistical learning theory di minimizzare il possibile errore sui dati del futuro andando in particolare a trovare l'iperpiano che separa i punti con margine geometrico massimo.

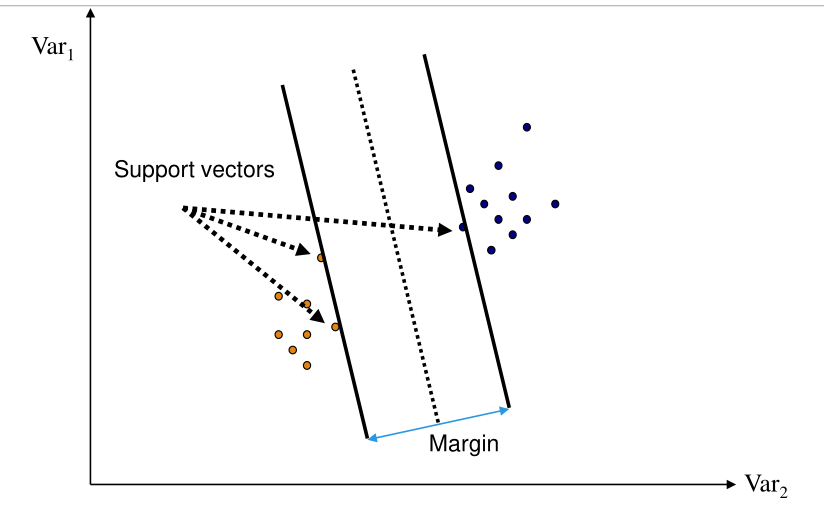
I punti alla frontiera dell'iperpiano desiderato si chiamano support vectors e che caratterizzano il margine dell'iperpiano.

Facendo poi varie trasformazioni e scalature avevamo ridotto il problema del calcolo dell'iperpiano con margine geometrico massimo alla risoluzione del seguente problema di ottimizzazione

\[\begin{split} &\underset{}{\min} \,\,\, \frac12 \cdot ||w||^2 \\ &\text{where } \\ & \;\;\;\; y_i(\overline{w} \cdot \overline{x} + b) \geq 1 \,\,,\,\,\, i = 1,\ldots,l \\ \end{split}\]

Abbiamo poi utilizzato il metodo di Lagrange per riformulare il problema e ottenere il seguente problema

\[\begin{split} &\underset{}{\max} \,\,\, \theta(\overline{\alpha}, \overline{\beta}) \\ &\text{where } \\ & \;\;\;\; \overline{\alpha} \geq \overline{0} \\ \end{split}\]

con

\[\theta(\overline{\alpha}, \overline{\beta}) = \text{inf}_{w \in W} L(\overline{w}, \overline{\alpha}, \overline{\beta})\]

e

\[L(\overline{w}, \overline{\alpha}, \overline{\beta}) = f(\overline{w}) - \sum\limits_{i = 1}^m \alpha_i g_i(\overline{w}) - \sum\limits_{i = 1}^l \beta_i h_i(\overline{w})\]

in cui

• \(f(\overline{w}) = \tau(\overline{w}) = \frac12 || \overline{w}||^2\)

• \(y_i((\overline{w} \cdot \overline{x}_i) + b) \geq 1\), per \(i = 1,\ldots,l\).

• I \(\beta_i\) non vengono utilizzati.

Per il nostro problem particolare troviamo

\[L(\overline{w}, \overline{\alpha}, b) = \frac12 \overline{w} \cdot \overline{w} - \sum\limits_{i = 1}^m \alpha_i [y_i (\overline{w} \cdot \overline{x}_i + b) - 1]\]

L'idea della nuova formulazione è quindi quello di penalizzare in termine di valore assunto le soluzioni che violano determinati vincoli. Così facendo stiamo trasferendo il concetto di vincolo al valore della funzione.

Osservazione 1: Passando al Lagrangiano rendiamo il calcolo della soluzione ottimale più efficiente. Nel problema originario infatti avevamo un vincolo per ogni punto del training set, e quindi testare se una possibile soluzione rispetta tutti i vincoli è computazionalmente faticoso. Nel problema duale invece abbiamo incorporato i vincoli nella funzione in sé, rendendo più efficiente il calcolo della soluzione.

Osservazione 2: La dualità sta quindi nel fatto che al posto di muovermi nello spazio dei parametri dell'iperpiano, mi muovo nello spazio dei valori di \(\overline{\alpha}\). Scegliere gli $$_i è un problema di campionamento tra i punti, scegliere il gradiente \(\overline{w}\) è un problema computazionalmente più difficile, in quanto ogni volta che sceglo una direzione devo verificare un vincolo per ogni punto.

---

Andando ad imporre le derivate della funzione \(L(\overline{w}, \overline{\alpha}, \overline{\beta})\) uguale a \(0\) otteniamo

• Rispetto a \(\overline{w}\)

  \[\frac{\partial L(\overline{w}, \overline{\alpha}, b)}{\partial \overline{w}} = \overline{w} - \sum\limits_{i = 1}^w y_i \alpha_i \overline{x}_i = \overline{x} \implies \overline{w} = \sum\limits_{i = 1}^m y_i \alpha_i \overline{x}_i\]

• Rispetto a \(b\)

  \[\frac{\partial L(\overline{w}, \overline{\alpha}, b)}{\partial b} = \sum\limits_{i = 1}^m y_i \alpha_i = 0\]

Notiamo che dalle soluzioni otteniamo che il punto di minimo è ottenuto tramite una combinazione lineare dei punti di training, ciascuno pesato con \(\alpha_i\), ovvero rispettivamente al contributo del vincolo associato al punto. Questo è esattamente quello che faceva il percettrone.

A questo punto sostituendo l'espressione trovata nella funzione obiettivo troviamo

\[\begin{split} L(\overline{w}, \overline{\alpha}, b) &= \frac12 \overline{w} \cdot \overline{w} - \sum\limits_{i = 1}^m \alpha_i\Big(y_i(\overline{w} \cdot \overline{x}_i + b) - 1 \Big) \\ &= \frac12 \sum\limits_{i,j = 1}^m y_i y_j \alpha_i \alpha_j \overline{x} \cdot \overline{x}_j - \sum\limits_{i, j = 1}^m y_i y_j \alpha_i \alpha_j \overline{x}_i \overline{x}_j + \sum\limits_{i = 1}^m \alpha_i \\ &= \sum\limits_{i = 1}^m \alpha_i - \frac12 \sum\limits_{i, j = 1}^m y_i y_j \alpha_i \alpha_j \overline{x}_i \overline{x}_j \\ \end{split}\]

Il problema di ottimizzazione diventa quindi

\[\begin{split} &\underset{}{\max} \,\,\, \sum\limits_{i = 1}^m \alpha_i - \frac12 \sum\limits_{i, j = 1}^m y_i y_j \alpha_i \alpha_j \overline{x}_i \overline{x}_j \\ &\text{where } \\ & \;\;\;\; \alpha_i \geq 0, i = 1,\ldots,m \\ & \;\;\;\; \sum_{i = 1}^m y_i \alpha_i = 0 \\ \end{split}\]

Osserviamo quindi che:

1. Ha una forma più semplice.

2. La formulazione dipende solamente dall'insieme delle variabili \(\alpha_i\), e non da \(\overline{w}\) e né da \(b\).

3. Rende esplicito il contributo individuale \((\alpha_i)\) di ciascun esempio del training set \(\overline{x}_i\).

Le seguenti condizioni sono dette condizioni di Lagrange

\[\begin{split} \frac{\partial L(\overline{w}^*, \overline{\alpha}^* \overline{\beta}^*)}{\partial \overline{w}} &= \overline{0} \\ \frac{\partial L(\overline{w}^*, \overline{\alpha}^* \overline{\beta}^*}{\partial \overline{\beta}} &= \overline{0} \\ \end{split}\]

vengono invece chiamate condizioni KKT le seguenti condizioni

\[\begin{split} \alpha_i^* g_i(\overline{w}^*) = 0 \;\;,\;\; i = 1,\ldots, m\\ g_i(\overline{w}^*) \leq 0 \;\;,\;\; i = 1,\ldots, m\\ \alpha_i^* \geq 0 \;\;,\;\; i = 1,\ldots, m\\ \end{split}\]

---

Dalle condizioni di Lagrange segue che

\[\sum\limits_{i = 1}^m \alpha_i y_i = 0 \;\;\;\;\;\; \overline{w} = \sum\limits_{i = 1}^m \alpha_i y_i \overline{x}_i\]

mentre dai vincoli KKT (Karush-Kuhn-Tucker) segue che

\[\alpha_i \cdot \Big[y_i(\overline{x}_i \cdot \overline{w} + b) - 1 \Big] = 0 \;\;\;\; i = 1,\ldots,m\]

In altre parole, i support vectors \(\overline{x}\) sonoo quelli con \(\alpha_i\) non nulli, ovvero tali che

\[y_i(\overline{x} \cdot \overline{w} + b) = - 1\]

Questi vettori si trovano nella frontiera.

Il valore \(b^*\) è calcolato nel seguente modo

\[b^* = - \frac{\overline{w}^* \cdot \overline{x}^+ + \overline{w}^* \cdot \overline{x}^-}{2}\]

dove \(\overline{x}^+\) è un generico esempio positivo, mentre \(\overline{x}^-\) è un generico esempio negativo.

Consideriamo una situazione in cui i dati in input non sono linearmente separabili.

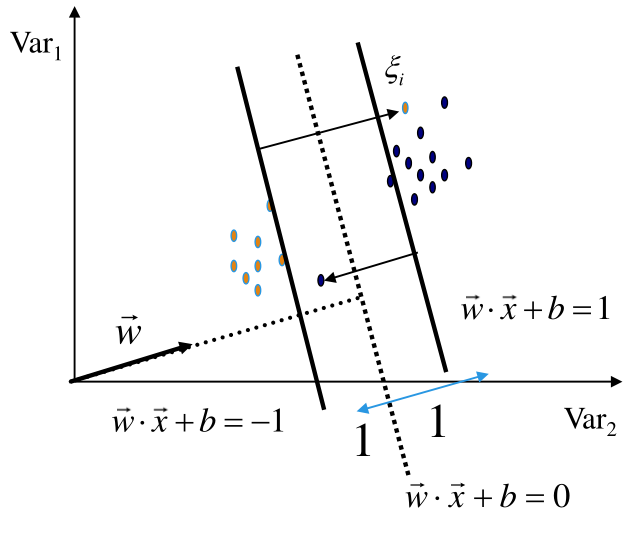
Per gestire questi casi posso utilizzare il procedimento di prima, andando però ad introdurre la possibilità di commettere degli errori. Formalmente questo viene fatto introducendo delle slack variables \(\xi_i\). In particolare i nuovi vincoli sono dati da

\[y_i(\overline{w} \cdot \overline{x}_i + b) \geq 1 - \xi_i\]

con \(\xi_i > 0\), e la nuova funzione obiettivo è data da

\[\min \frac12 || \overline{w} ||^2 + C \cdot \sum_i \xi_i\]

dove la costante \(C\) è il trade-off tra il margine richi. Dato poi che gli errori possono essere sia da un lato che dall'altro, in realtà al posto di considerare l'errore in sé consideriamo la somma degli errori quadratici \(\sum_i \xi_i^2\).

---

In particolare troviamo quindi la seguente formulazione

\[\begin{cases} \text{min} \;\; ||\overline{w}|| + C \cdot \sum\limits_{i = 1}^m \xi_i^2 \\ \\ y_i(\overline{w} \cdot \overline{x}_i + b) \geq 1 - \xi_i, \;\;\; \forall i = 1,\ldots,m \\ \xi_i \geq 0, \;\;\; \forall i = 1,\ldots,m \\ \end{cases}\]

Considerando il Lagrangiano otteniamo la seguente funzione

\[L(\overline{w}, b, \overline{\xi}, \overline{\alpha}) = \frac12 \overline{w} \cdot \overline{w} + \frac{C}{2} \sum\limits_{i = 1}^m \xi_i^2 - \sum\limits_{i = 1}^m \alpha_i [ y_i (\overline{w} \cdot \overline{x}_i + b) - 1]\]

Andando a derivare otteniamo,

rispetto a \(\overline{w}, \overline{\xi}\) e \(b\) otteniamo

• Rispetto a \(\overline{w}\),

  \[\frac{\partial L(\overline{w}, b, \overline{\xi}, \overline{\alpha})}{\partial \overline{w}} = \overline{w} - \sum\limits_{i = 1}^m y_i \alpha_i \overline{x}_i = \overline{0} \implies \overline{w} = \sum\limits_{i = 1}^m y_i \alpha_i \overline{x}_i\]

• Rispetto a \(\overline{\xi}\),

  \[\frac{\partial L(\overline{w}, b, \overline{\xi}, \overline{\alpha})}{\partial \xi} = C \overline{\xi} - \overline{\alpha} = \overline{0}\]

• Rispetto a \(b\),

  \[\frac{\partial L(\overline{w}, b, \overline{\xi}, \overline{\alpha})}{\partial b} = \sum\limits_{i = 1}^m y_i \alpha_i = 0\]

Sostituendo alla funzione obiettivo troviamo quindi la seguente formula

\[\sum\limits_{i = 1}^m \alpha_i - \frac12 \sum\limits_{i, j = 1}^m y_i y_j \alpha_i \alpha_j (\overline{x}_i \overline{x}_j + \frac{1}{C} \delta_{i, j})\]

dove \(\delta_{i, j}\) è la delta di Kronecker.

La forma finale del problema duale è quindi al seguente

\[\begin{split} &\underset{}{\max} \,\,\, \sum\limits_{i = 1}^m \alpha_i - \frac12 \sum\limits_{i, j = 1}^m y_i y_j \alpha_i \alpha_j \Big( \overline{x}_i \overline{x}_j + \frac{1}{C} \delta_{i, j} \Big)\\ &\text{where } \\ & \;\;\;\; \alpha_i \geq 0, i = 1,\ldots,m \\ & \;\;\;\; \sum_{i = 1}^m y_i \alpha_i = 0 \\ \end{split}\]

Notiamo che anche quando i dati sono linearmente separabili rilassare il vincolo sull'hard margin potrebbe dare risultati migliori.

Consideriamo il seguente esempio

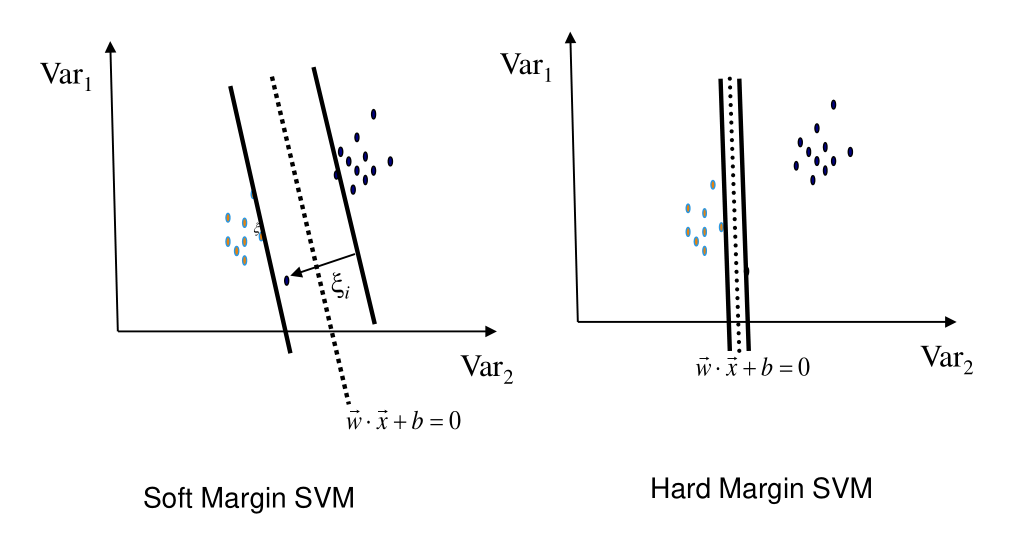
Dato che i dati sono linearlmente separabili, possiamo effettivamente calcolare l'iperpiano che separa esattamente i punti. Notiamo però che questa soluzione è molto più rischiosa, e non sembra catturare bene la separazione tra i dati futuri.

In generale un soft-margin SVM ha sempre una soluzione, ed è più robusto rispetto a degli esempi odd del training set. Questo in particolare è utile quando, ad esempio, ho un campionamento insufficiente nel training, oppure ho un elevato grado di ambiguità tra le features.

Viceversa però le hard-margin SVM non hanno parametri.