WMR 20 - Clustering
Lecture Info
Date:
Course Site: Web Mining e Retrieval (a.a. 2019/20)
Lecturer: Danilo Croce.
Slides: ()
Table of Contents:
1 Clustering and Unsupervised Learning
Fino a questo momento abbiamo sempre trattato di casi di supervised learning, ovvero casi in cui degli esseri umani sono in grado di costruire il dataset di training, che contiene sia i dati che le etichette per ogni dato. Questo tipo di processo tendenzialmente è molto costoso.
Per cercare di ottimizzare i costi è possibile quindi utilizzare dei diversi approcci all'apprendimento. Tra questi troviamo l'approccio unsupervised, caratterizzato dal fatto che i dati utilizzati per apprendere non sono etichettati.
Uno dei primi scenari in cui è possibile applicare questo tipo di apprendimento è il marketing, in cui si utilizzano i dati di acquisto dei clienti per andare a catturare i diversi tipi di clienti possibili. Questi gruppi disgiunti di esempi sono tipicamente chiamati clusters.
Storicamente il clustering, ovvero l'attività di dividere dei dati non etichettati in gruppi in cui gli elementi in ciascun gruppo sono simili tra loro, ed elementi facenti parte di gruppi diversi sono tra loro diversi, è considerato equivalente all'unsupervised learning.
1.1 Hierarchical Clustering
Olte a raggruppare i vari elementi in clusters, potrei anche essere interessati a scoprire delle possibili gerarchie tra i vari clusters.
Consideriamo ad esempio la seguente struttura alborea, chiamata dendrogramma, che rappresenta tassonomia degli animali
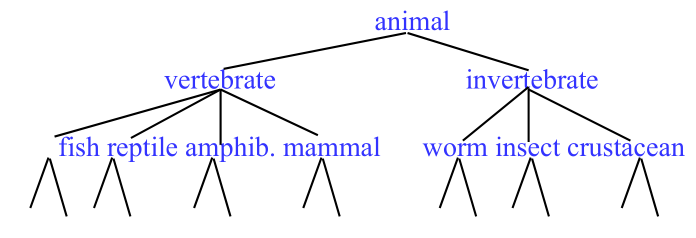
Questo tipo di struttura può essere costruita utilizzando in modo ricorsivo tecniche di clustering.
1.2 Direct Clustering
I metodi di direct clustering necessitano di specificare il numero di cluster desiderati \(k\) e i punti da clusterizzare.
È anche necessario definire una clustering evaluation function, che assegna un numero reale che misura la "qualità" di ciascun clustering.
1.3 Aspects of Clustering
La qualità di un clustering dipende da vari aspetti, tra cui troviamo i seguenti:
Clustering algorithm:
Single Link Agglomerative Clustering.
K-Means
...
Distance (similarity or dissimilarity) function.
Clustering quality:
Inter-clusters distance (to maximize).
Intra-clusters distance (to minimize)
1.4 Agglomerative/Divise Hierarchical Clustering
Gli algoritmi di clustering gerarchici possono essere di due tipi:
Agglomerative (bottom-up): inizialmente ciascun esempio rappresenta un cluster separato, e in modo iterativo questi clusters sono combinati tra loro per formare clusters più grandi.
Divisive (partitional, top-down): Inizialmente tutti gli esempi formano un singolo grande cluster, la radice, e in modo ricorsivo i clusters sono divisi tra loro in un insieme di clusters-child.
2 Hierarchical Agglomerative Clustering (HAC)
Questo algoritmo di clustering inizia con tutti gli esempi che formano clusters diversi, e in modo iterativo combina i due clusters che sono più simili assieme fino a quando rimane un solo cluster. La storia dei merging crea la struttura alborea vista prima.
Per fare questo utilizza una funzione di similarità. Il modo in cui si utilizza questa funzione per calcolare la similarità tra due clusters, è diverso, e può essere:
Single link: Similarity of two most similar members.
\[\text{sim}(c_i, c_j) = \underset{x \in C_u, \; y \in C_j}{\text{max}} \text{sim}(x, y)\]
Complete link: Similarity of two least similar members.
\[\text{sim}(c_i, c_j) = \underset{x \in C_u, \; y \in C_j}{\text{min}} \text{sim}(x, y)\]
Group average: Average similarity between members.
\[\text{sim}(c_i, c_j) = \frac{1}{|C_i \cup C_j| \cdot (|C_i \cup C_j| - 1) } \cdot \sum\limits_{x \in (C_i \cup C_j)} \;\; \sum\limits_{y \in (C_i \cup C_j): y \neq x} \text{sim}(x, y)\]
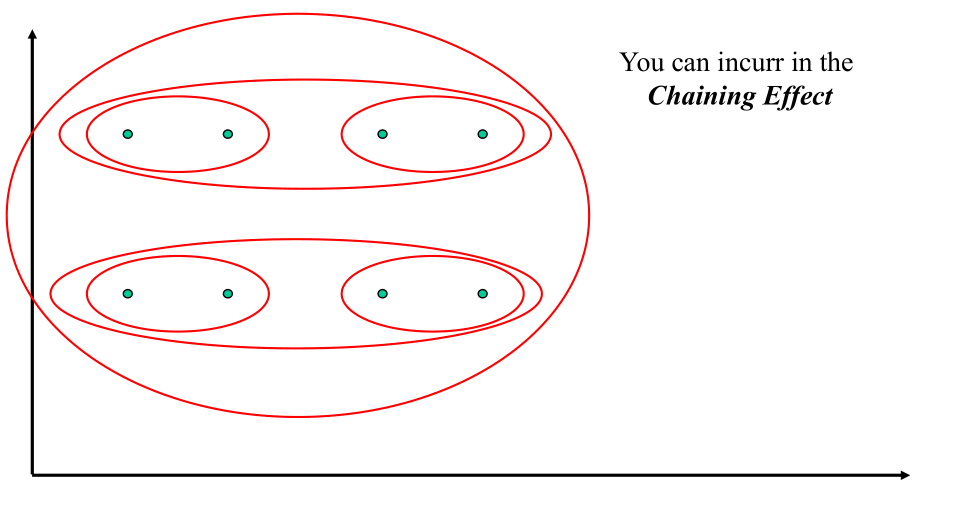
2.1 Chaining Effect
Utilizzando il link link si può cadere in un fenomeno noto come il chaining effect, in cui essenzialmente fondo tutti i clusters, uno alla volta, in un singolo cluster che diventa sempre più grande.
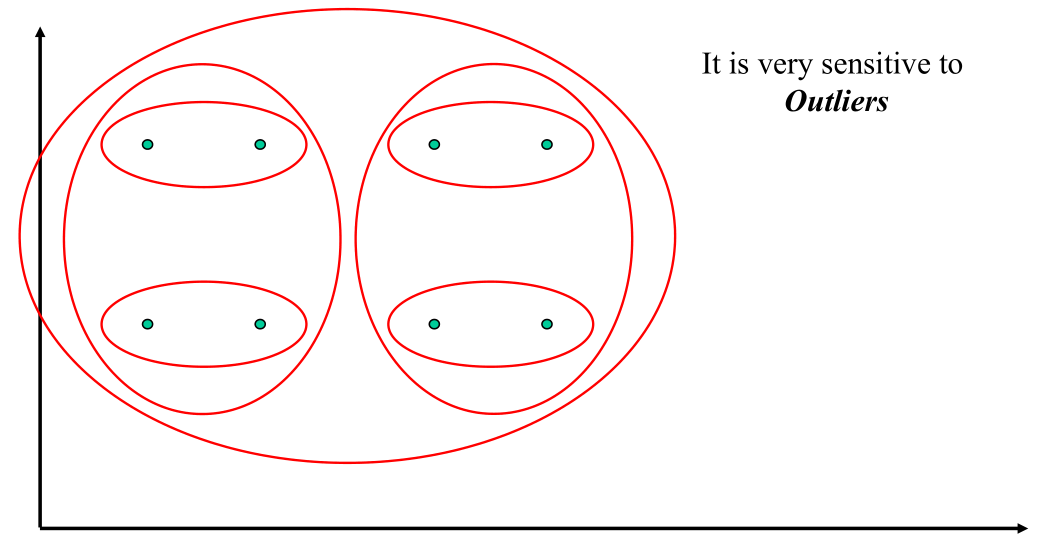
2.2 Complete Link Example
Il complete link è molo sensibile alla presena di outliers
2.3 Computational Complexity
Nella prima iterazione tutti i metodi HAC devono calcolare la similarità per ogni coppia di \(n\) punti individuali, il costo computazionale è quindi di \(O(n^2)\). Nei successivi \(n-1\) iterazioni di marging, bisogna comunque calcolare la distanza tra tutti i cluster esistenti.
Questo significa che per avere una overall performance di \(O(n^2)\), il calcolo della similarità deve essere fatto in tempo costante. Esistono però dei trucchi per rendere più efficiente il calcolo della similarità
Supponiamo di lavorare in uno spazio normalizzato, e consideriamo la cosine similarity come misura di similarità.
\[\text{cos(x, y)} = \frac{x \cdot y}{||x||_2 \cdot ||y||_2}\]
Se mantengo per ogni cluster la somma dei vettori
\[\overline{s}(c_j) = \sum\limits_{\overline{x} \in C_j} \overline{x}\]
il calcolo della similarità tra cluster diventa costante, in quanto la posso calcolare come segue
\[\text{sim}(C_i, C_j) = \frac{\Big(\overline{s}(C_i) + \overline{s}(C_j) \Big) \cdot \Big(\overline{s}(C_i) + \overline{s}(C_j) \Big) - (|C_i| + |C_j|)}{(|C_i| + |C_j|)(|C_i| + |C_j| - 1)}\]
3 Non-Hierarchical Clustering
Andiamo adesso a vedere degli algoritmi di clustering non gerarchici. Per questi algoritmi si fissa il numero \(k\) di cluster desiderati. L'idea principale è poi quella di scegliere in modo randomico \(k\) istanze come seeds, uno per cluster, e in modo iterativo si associano i vari elementi ai vari cluster, fino ad arrivare ad una situazione di convergenza (misurata in qualche modo).
3.1 K-Means
Un esempio di algoritmo di clustering non gerarchico è il K-Means, che funziona nel seguente modo.
Siano \(d\) la misura di distanza tra le varie istanze. Inizialmente si selezionano \(k\) random istances \(\{s_1, s_2, \ldots, s_k\}\) come seeds, e si esegue il seguente codice fino a soddisfare il criterio di convergenza:
Until clustering converges:
For each instance x_i:
Assign x_i to the cluster c_j such that d(x_i, s_j) is minimal
# update centroid of each cluster
For each cluster c_j
s_j = \mu(c_j)
Generalmente i centroidi sono dei punti virtuali e sono calcolati tramite la media. Quando però non possiamo calcolare la media l'idea è quella di utilizzare il medoide, ovvero il punto preso dai punti di training che si avvicina il più possibile a tutti gli altri dello stesso cluster.
Il criterio di convergenza del K-Means è basato su quanti riassegnamenti ho dei vari punti ai vari clusters. Ad esempio mi potrei fermare quando non faccio cambiare cluster a nessun punto, oppure in modo rilassato quando faccio cambiare cluster solamente ad un punto.
L'algoritmo K-Means garantisce che alla terminazione ho minimizzato la summa dello squared error (SSE), che nel caso in cui sto considerando delle distanze ottengo
\[\text{SSE} = \sum\limits_{j = 1}^k \sum\limits_{x \in C_j} \text{dis}(x, m_j)^2\]
dove \(m_J\) è il centroide del cluster \(C_j\).
Il caviat di questo risultato è che il minimo menzionato non è un minimo globale, ma solo locale, e dipende dal punto da cui parto.
3.1.1 Time Complexity
Assumendo di avere vettori con \(m\) dimensioni, il calcolo della distanza richiede \(O(m)\) passi.
La riassegnazione del clusters invece costa \(O(kn)\) computazioni della distanza, e quindi in totale \(O(knm)\).
Il calcolo dei centroidi invece \(O(nm)\).
Se infine assumiamo che abbiamo in totale \(I\) iterazioni, otteniamo una complessità \(O(lknm)\). Questo significa che assumendo un numero fissato di operazioni, abbiamo un costo più efficiente di un algoritmo di tipo HAC (che è \(O(n^2)\)).
3.1.2 Problems
Il K-means presenta i segueti problemi:
L'algoritmo così definito è applicabile solamente se la media è definita ed è calcolabile.
L'algoritmo è sensibile agli outliers.
L'utente deve specificare \(k\).
I risultati possono variare di molto rispetto alla selezione randomica dei seed.
Alcuni seed possono rendere l'algoritmo significativamente più lento del solito.
Tra tutti questi il problema principale del K-means però è la sensibilità agli outliers
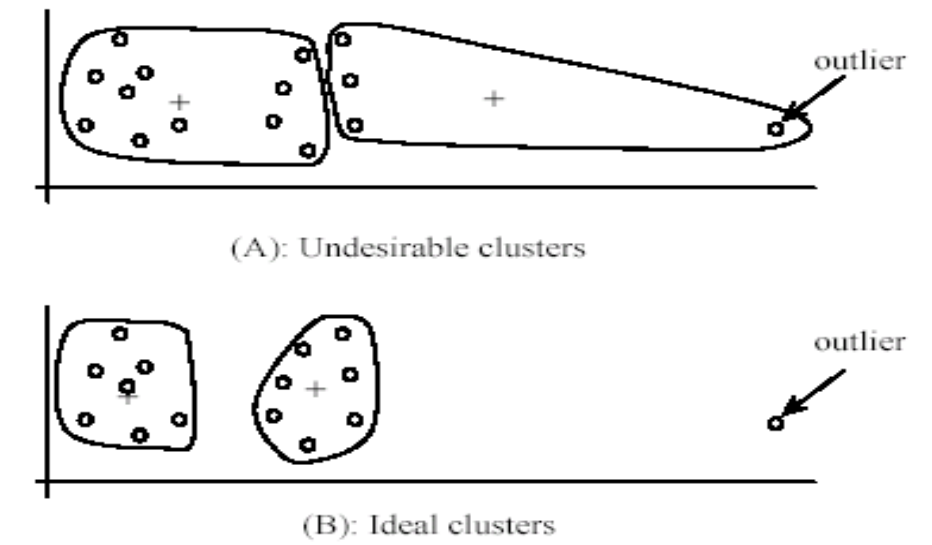
3.2 QT K-Means
Modifica del tipico K-Means con la possibilità di aggiungere/rimuovere clusters durante l'esecuzione.
Segue lo speudocodice:
Let \sigma and \tau be two different thresholds
Let d be the distance measure
Select k random seeds {s_1, \ldots, s_k}
Until clustering converges
For each instance x_i
Assign x_i to cluster c_j such that d(x_i, s_j) is minimize but less than \sigma
Else create new seed with instance x_i (new cluster, k increases)
For each cluster pair c_i, c_j such that i \neq j:
If d(s_i, s_j) is less than \tau, merge c_i and c_j (k decreases)
4 Distance Metrics
Notiamo a questo punto che sono varie le possibili funzioni che possiamo utilizzare per calcolare la distanza. Tra queste troviamo:
Distanza euclidea (\(L_2\) norm):
\[L_2(\overline{x}, \overline{y}) \sum\limits_{i = 1}^m (x_i - y_i)^2\]
\(L_1\) norm:
\[L_1(\overline{x}, \overline{y}) = \sum\limits_{i = 1}^m |x_i - y_i|\]
Cosine similarity (trasformata in distanza)
\[1 - \text{cos}(\overline{x}, \overline{y}) = 1 - \frac{\overline{x} \cdot \overline{y}}{|\overline{x}| \cdot | \overline{y} |}\]
5 Data Standardization
Supponiamo di stare in uno spazio euclideo a due dimensioni, in cui la prima dimensione varia tra \(0\) e \(1\), mentre la seconda tra \(0\) e \(1000\). Calcolando la distanza tra due punti notiamo che la seconda coordianta domina completamente il valore della distanza. Ad esmepio
\[\text{dist}(x_i, x_j) = \sqrt{(0.9 - 0.1)^2 + (720 - 20)^2} = 700.000457\]
Per cercare di risolvere questo problema l'idea è quella di efettuare una standardizzazione degli attributi, ovvero si forzano gli attributi delle istanze di training ad avere un common value range.
5.1 Interval-Scaled Attributes
Quando si parla di interval-scaled attribute si sta parlando di attributi il cui valore è racchiuso in un intervallo della retta reale.
Sia \(f\) un attributo. Esistono due approcci principali per standardizzare questo tipo di attributi, che sono:
Range:
\[\text{range}(x_{i,f}) = \frac{x_{i,f} - \text{min}(f)}{\text{max}(f) - \text{min}(f)}\]
Z-score: L'idea è quella di trasformare i valori degli attributi in modo tale da avere una media di \(0\) e una mean absolute deviation di \(1\).
\[\begin{split} s_f &= \frac{1}{n}\Big( |x_{1,f} - m_f | + | x_{2,f} - m_f | + \ldots + | x_{n,f} - m_f | \Big) \\ m_f &= \frac{1}{n}\Big(x_{1,f} + x_{2,f} + \ldots + x_{n,f} \Big)\\ z(x_{i,f}) &= \frac{x_{i,f} - m_f}{s_f} \end{split}\]
6 Cluster Evaluation
Il vero problema nel contesto del clustering è proprio la valutazione delle performance del cluster trovato. Infatti, lavorando in un setting non supervisionato, è difficile trovare delle metriche ci dicono quanto ragionevole e buono è il clustering trovato.
In generale possiamo utilizzare queste tre strategie:
Internal criteria: misurare qualche criterio interno intrinseco del dataset e del clustering ottenuto.
External criteria: si utilizza un gold standard o un evaluation benchmark.
Indirect evaluation criteria: Molto spesso il clustering è utilizzato in altri task, e quindi stabilire come sta andando il task esterno permette di capire in modo indiretto la qualità del clustering ottenuto.
6.1 External Criteria
Se abbiamo a disposizione dei dati etichettati (per la classificazione), possiamo assumere che ciascun cluster è una classe, calcolare la confusion matrix, e calcolare le solite varie metriche tra cui Precision, Recall, F-score.
Possiamo stimare \(P_i(C_j)\), ovvero la proporzione di data points appartenenti alla classe \(C_j\) nel cluster \(i\)
\[P_i(C_j) = \frac{| C_j \cap D_i |}{|D_i|}\]
6.1.1 Purity
Un'altra misura è la purity. La purity di ciascun cluster è calcolata come segue
\[\text{purity}(D_i) = \text{max}_j P_i(C_j)\]
La purity totale dell'intero clustering è quindi calcolata come segue
\[\text{purity}_{\text{total}}(D) = \sum\limits_{i = 1}^k \frac{|D_i|}{|D|} \times \text{purity}(D_i)\]
Problemi della purity: All'aumentare del numero di \(k\) la purity tende sempre ad \(1\). Dunque non può essere utilizzata per stimare \(k\).
6.1.2 Entropy
Un altro modo è quello di calcolare l'entropia per ogni cluster come segue
\[\text{entropy}(D_i) = - \sum\limits_{j = 1}^k P_i(C_j)\log_2{P_i(C_j)}\]
L'entropia totale è quindi la seguente
\[\text{entropy}_{\text{total}} \sum\limits_{i = 1}^k \frac{|D_k|}{|D|} \times \text{entropy}(D_i)\]
Il problema di questo è il fatto che per calcolare l'entropia devo
7 Soft Clustering
Fino adesso abbiamo visto un hard clustering, ovvero un clustering in cui ciascun elemento può appartenere ad uno e un solo cluser. Sono stati poi definiti dei metodi di soft clustering, in cui il risultato non è un'assegnazione fissa ma una distribuzione di probabilità di appartenere ai vari clustering.
Un esempio di questo tipo di clustering è il Fuzzy C-mean.
8 Subspace Clustering (LAC)
Locally Adapctive Clustering.