WMR 21 - Kernel Methods I
Lecture Info
Date:
Course Site: Web Mining e Retrieval (a.a. 2019/20)
Lecturer: Roberto Basili.
Slides: ()
Table of Contents:
In questa lezione abbiamo introdotto il concetto di funzione kernel a partire dalla formulazione duale della funzione di classificazione ottenuta per le SVMs.
1 SVMs and Scalar Product
Rispetto alle reti neurali le SVM costituiscono dei percettroni, ovvero tendono a promuovere leggi lineari tramite la minimizzazione dell'errore atteso
\[h(x) = \text{sign}(\overline{w} \cdot \overline{x} + b) = \text{sign}\Bigg( \sum\limits_{j = 1}^l a_j y_j \overline{x}_j \cdot \overline{x} + b\Bigg)\]
Durante la trattazione avevamo poi introdotto le soft-SVM per gestire tutti quei casi in cui i dati di input non sono linearmente separabili.
Un'altro possibile approccio per gestire questa situazione è quella di cambiare lo spazio di rappresentazione delle istanze. In particolare possiamo utilizzare una funzione \(\phi\) per proiettare le istanze di training in uno spazio più complesso con più dimensioni. In questo nuovo spazio i dati potrebbero nuovamente essere linearmente separabili. Questo approccio alternative apre le porte ai metodi kernel.
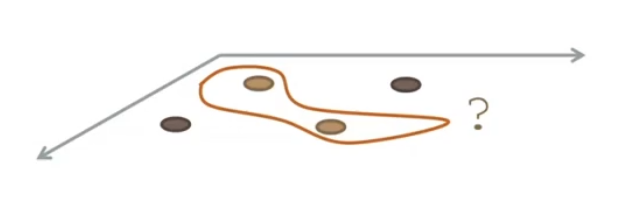
Consideriamo ad esempio il seguente spazio di partenza. Come è possibile vedere, i punti non sono linearmente separabili.
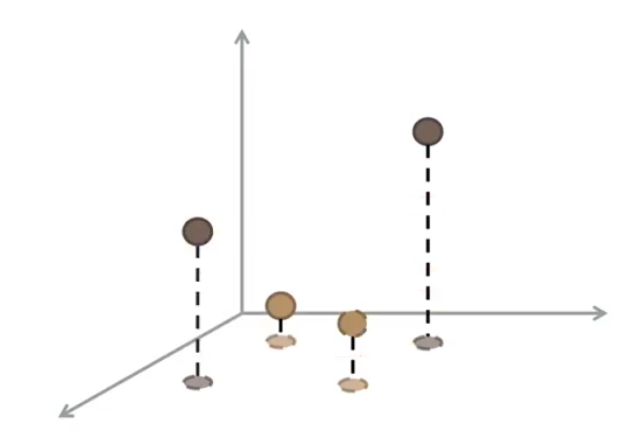
Se però effettuiamo una trasformazione e passiamo ad un nuovo spazio
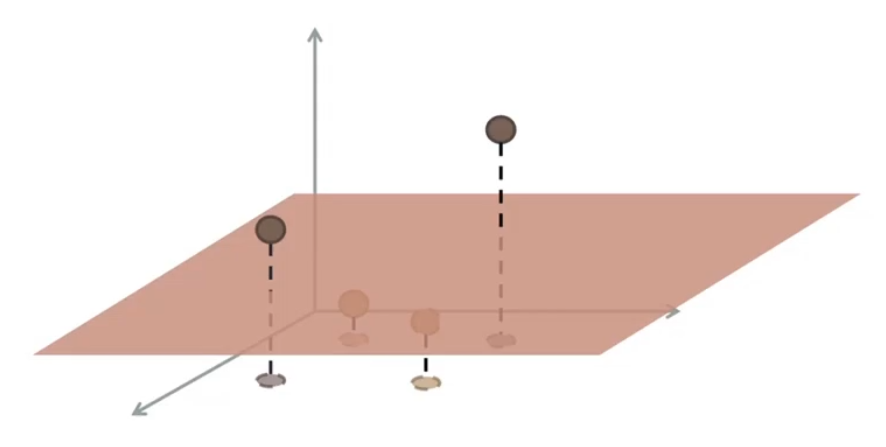
Ecco che i punti diventano linearmente separabili nel nuovo spazio.
I metodi kernel si basano sulla forma duale della funzione segno. Possiamo infatti vedere un classificatore SVM sia come ottenuto dai parametri della retta \(\overline{w}\) e del termine noto \(b\), e sia come ottenuto dagli altri elementi del training set nella seguente combinazione lineare.
\[\text{sign}\Bigg( \sum\limits_{j = 1}^l a_j y_j \overline{x}_j \cdot \overline{x} + b\Bigg)\]
Notiamo che per utilizzare il modello con questa seconda formulazione ci basta solamente sapere il valore del prodotto scalare tra \(\overline{x}_j\) e \(\overline{x}\), senza neanche necessariamente sapere i vettori veri e propri. In altre parole, necessitiamo solamente il valore del prodotto scalare.
2 Kernel Function
In generale chiamiamo un kernel una funzione della seguente forma
\[K(\overline{x}, \overline{z}) = \Phi(\overline{x}) \cdot \Phi(\overline{z})\]
Il kernel corrisponde quindi al prodotto scalare calcolato in base ai vettori \(x\) e \(z\) nel nuovo spazio vettoriale fornito da \(\Phi\). Quando poi \(\Phi\) corrisponde alla funzione identità, il kernel equivale al prodotto scalare standard.
Molto spesso la funzione kernel viene calcolata senza utilizzare esplicitamente la trasformazione \(\Phi\).
Per ogni coppia di punti presi dal training set \(\overline{x}_i, \overline{x}_j\) calcolando il valore \(K(\overline{x}_i, \overline{x}_j)\) è possibile formare una matrice quadrata chiamata Gram-matrix.
Tra i vantaggi nell'utilizzo delle kernel functions troviamo sicuramente il seguente: making instances linearly separable

Osservazione: L'approccio Kernel rappresenta una strada alternativa all'apprendimento, in cui, al posto di rendere più complessa la funzione di classificazione, rendiamo più complesso lo spazio di rappresentazione delle istanze di training.
2.1 Example
Consideriamo due oggetti, uno con massa \(m_1\) e l'altro con massa \(m_2\), e applichiamo una forza \(f_a\) alla massa \(m_1\) e cerchiamo di capire quanto deve essere grande \(f_a\) per far muovere uno dei due oggetti. Il task in particolare corrisponde a determinare quando
\[f(m_1, m_2, r) < f_a\]
Come è intuibile, per risolvere questo problema è coinvolta la legge gravitazionale di Netwon
\[f(m_1, m_2, r) = C \cdot \frac{m_1 m_2}{r^2}\]
Nello spazio iniziale questo problema di classificazione non può essere espreso linearmente. Possiamo però trasformare lo spazio, applicando la seguente trasformazione
\[(f_a, m_1, m_2, r) \to (k, x, y, z) = (\ln f_a, \; \ln m_1, \; \ln m_2, \; \ln r)\]
Soddisfare la legge nel nuovo spazio significa quindi soddisfare la seguente funzione
\[\ln f(m_1, m_2, r) = \ln C + \ln m_1 + \ln m_2 - 2 \ln r = c + x + y -2z\]
La funzione di classificazione è quindi espressa dal seguente iperpiano
\[(1, 1, -2, -1) \cdot (\ln m_1, \ln m_2, \ln r, \ln f_a) + \ln C = 0\]
Così facendo abbiamo ricondotto una legge non lineare ad una lineare andando a cambiare lo spazio di input.
2.2 Feature Spaces
Per parlare meglio dei metodi kernel è necessario introdurre la seguente distinzione tra spazi di dati:
Input space: Lo spazio iniziale dei dati del training set.
Feature space: Lo spazio mappato a partire dall'input space tramite la trasformazione (eventualmente non lineare) \(\phi: R^N \to F\). Su questo spazio deve essere definito il prodotto scalare.
Graficamente,
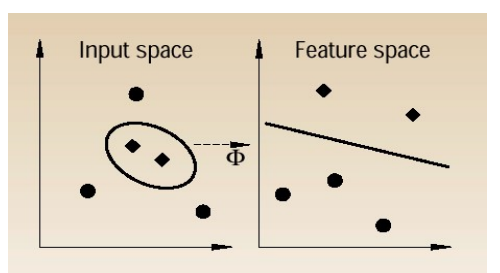
La funzione kernel è definita sullo spazio di input ed è definita nel seguente modo
\[k(x, y) = \phi(x) \cdot \phi(y)\]
2.3 Gram-Matrix
Dato la forma duale della funzione di classificazione dipende solamente dai prodotti scalari
\[h(x) = \text{sign}\Bigg(\sum\limits_{j = 1}^l \alpha_j y_j \overline{x}_j \cdot \overline{x} + b \Bigg)\]
L'unica cosa che mi serve per effettuare l'apprendimento del modello sono i valori dei prodotti scalari. La Gram matrix contiene esattamente questi valori
\[G = \Big( (\overline{x}_i \cdot \overline{x}_j) \Big)_{i, j = 1}^l\]
2.4 Kernelixed Perceprton
È possibile modificare la funzione di classificazione di un percettrone andando ad aggiungere una funzione kernel \(h(x, y)\) nel seguente modo
\[\begin{split} h(x) &= \text{sign}(\overline{w} \cdot \Phi(\overline{x}) + b) \\ &= \text{sign} \Big(\sum\limits_{j = 1}^l \alpha_j y_j \Phi(\overline{x}_j) \cdot \Phi(\overline{x}) + b \Big) \\ &= \text{sign}\Big(\sum\limits_{j = 1}^l \alpha_j y_j k(\overline{x}_j, \overline{x}) + b \Big) \\ \end{split}\]
Durante il training quindi il passo di update diventa il seguente
\[y_i \Big(\sum\limits_{j = 1}^l \alpha_j y_j \Phi(\overline{x}_j) \cdot \Phi(\overline{x}_i) + b \Big) = \sum\limits_{j = 1}^l \alpha_j y_j y_i k(\overline{x}_j, \overline{x}_i) + b\]
3 Kernel in SVMs
Nella versione soft delle SVMs dobbiamo ottimizzar ela seguente funzione
\[\sum\limits_{i = 1}^m \alpha_i - \frac12 \sum\limits_{i, j = 1}^m y_i y_j \alpha_i \alpha_j \overline{x}_i \cdot \overline{x}_j + \frac{1}{2C} \overline{\alpha} \cdot \overline{\alpha} - \frac{1}{C} \overline{\alpha} \cdot \overline{\alpha}\]
Aggiungendo la funzione kernel \(k(\cdot, \cdot)\) otteniamo il seguente problema
\[\begin{split} &\underset{}{\max} \,\,\, \sum\limits_{i = 1}^m \alpha_i - \frac12 \sum\limits_{i, j = 1}^m y_i y_j \alpha_i \alpha_j \Big(k(o_i, o_j) + \frac{1}{C} \delta_{i, j}\Big) \\ &\text{where } \\ & \;\;\;\; \alpha_i \geq 0, \;\; \forall i = 1,\ldots,m \\ & \;\;\;\; \sum\limits_{i = 1}^m y_i \alpha_i = 0 \\ \end{split}\]
Dove \(o_i\) e \(o_j\) sono gli elementi dello spazio di input.
L'architettura di un SVM con kernel è quindi la seguente
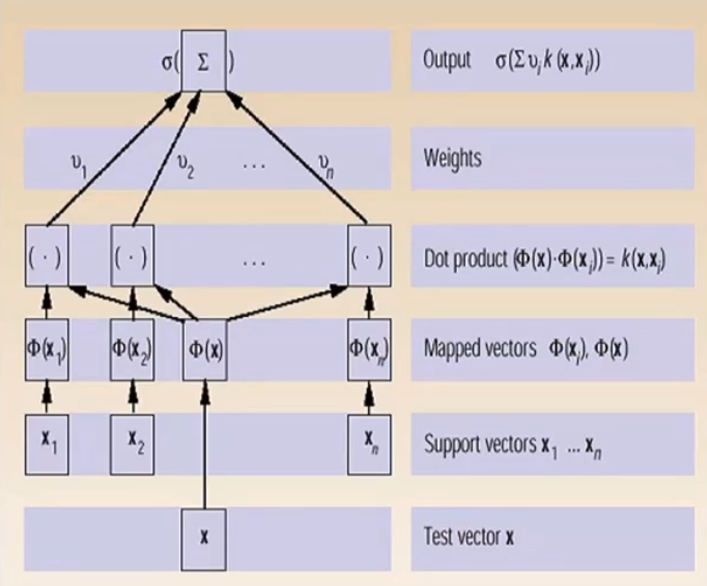
4 Finding Kernels
Per definizione avevamo detto che una funzione \(k\) è detta kernel function quando \(\forall \overline{x}, \overline{z} \in X\), si ha che
\[k(\overline{x}, \overline{z}) = \Phi(\overline{x}) \cdot \Phi(\overline{z})\]
dove \(\Phi\) è un mapping da \(X\) ad particolare feature space in cui è ben definito il prodotto scalare.
Consideriamo adesso alcune caratteristiche che la Gram-Matrix costruita a partire da una funzione kernel \(k\) deve avere:
Symmetric Matrix: Deve essere simmetrica, in quanto il prodotto scalare è simmetrico.
Positive (Semi-) definite Matrix: I suoi autovalori devono essere tutti positivi (o al più non-negativi).
Se abbiamo che la nostra Gram matrix è semi-definita positiva, allora so sicuramente che esiste uno spazio delle features \(F\) su cui è definito un prodotto scalare. In \(F\) la separabilità delle istanze di input dovrebbe essere più semplice.
5 Kernel Examples
Andiamo adesso a vedere qualche esempio esplicito di funzione kernel.
5.1 The Polynomial Kernel
Consideriamo la seguente funzione
\[k(x, y) = (x \cdot y)^d\]
Se \(d=2\) otteniamo
\[\begin{split} (x \cdot y)^2 &= \Bigg( \begin{bmatrix} x_1 \\ x_2 \\ \end{bmatrix} \cdot \begin{bmatrix} y_1 \\ y_2 \\ \end{bmatrix} \Bigg)^2 \\ &= \Bigg( \begin{bmatrix} x_1^2 \\ \sqrt{2} x_1 x_2 \\ x_2^2 \\ \end{bmatrix} \cdot \begin{bmatrix} y_1^2 \\ \sqrt{2} y_1 y_2 \\ y_2^2 \\ \end{bmatrix} \Bigg) \\ &= (\Phi(x) \cdot \Phi(y)) = k(x, y) \end{split}\]
Notiamo che così facendo abbiamo ricondotto il calcolo del prodotto scalare tra i vettori trasformati a delle operazioni sulle coordinate nello spazio di partenza.
Se invece lavoriamo con \(n\) dimensioni otteniamo la seguente espressione
\[\begin{split} (\overline{x} \cdot \overline{z})^2 = \Big(\sum\limits_{i = 1}^n x_i z_i \Big)^2 &= \Big(\sum\limits_{i = 1}^n x_i z_i \Big) \Big(\sum\limits_{i = 1}^n x_i z_i \Big) \\ &= \sum\limits_{i = 1}^n \sum\limits_{j = 1}^n x_i x_j z_i z_j \\ &= \sum\limits_{i, j \in \{1, \ldots, n\}} (x_i x_j) (z_i z_j) \\ &= \sum\limits_{k = 1}^m X_k Z_k \\ &= \overline{X} \cdot \overline{Z} \end{split}\]