WMR 23 - Lab III (Tree Kernels + KeLP)

Consideriamo un problema di classificazione binaria in cui abbiamo uno spazio di rappresentazione delle istanze di input \(X \subseteq \mathbb{R}^n\) e un output space \(Y = \{-1, 1\}\). Il training set è quindi dato da

\[S = \{(x_1, y_1), \ldots, (x_l, y_l)\} \subset (X \times Y)\]

Il nostro obiettivo è quello di trovare una funzione \(f: X \subseteq \mathbb{R}^n \to \mathbb{R}\) e, a partire da questa, definire il nostro classificatore binario come la funzione segno di \(f\)

\[\text{sign}(f(x)) = \begin{cases} 1 \;\;&,\;\; f(x) \geq 0 \\ -1 \;\;&,\;\; f(x) < 0 \\ \end{cases}\]

---

In particolare consideriamo la seguente istanza

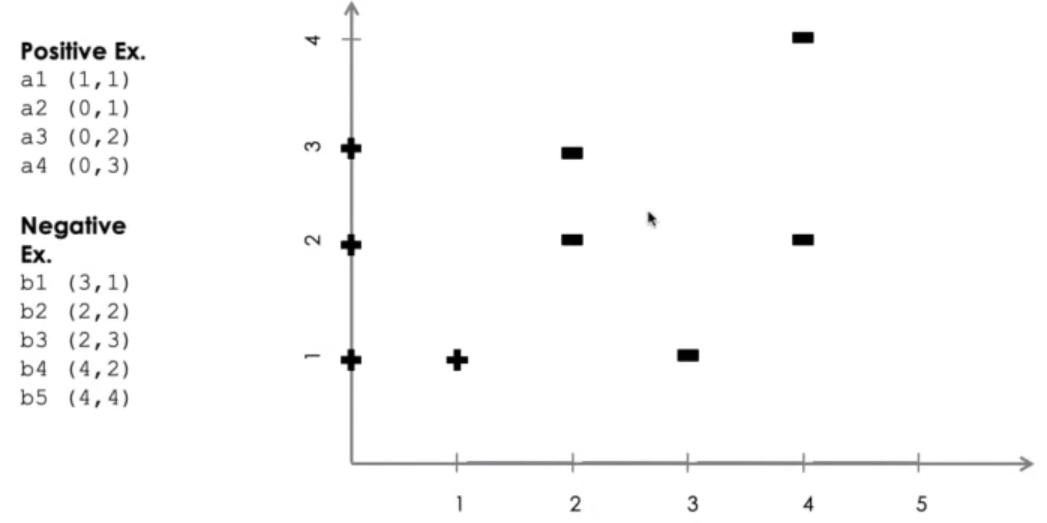
Una volta applicato un algoritmo di SVM otteniamo il seguente risultato

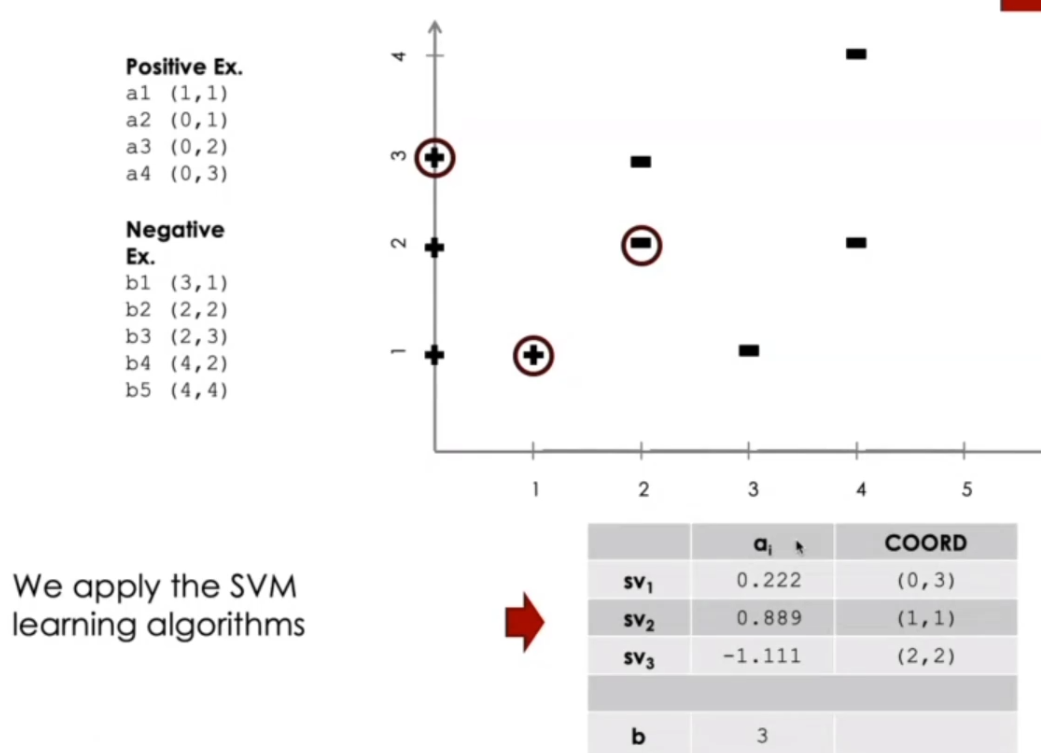
Notiamo che l'output del processo di learning per una macchina SVM corrisponde ad una serie di dati associati a ciascun support vector \(\text{sv}_i\). Per ottenere le coordiante a partire da ciascun output devo, in generale, calcolare le seguenti quantità

\[\begin{split} \overline{w} &= \sum\limits_{i = 1}^m \alpha_i \cdot y_i \overline{x}_i \\ b &= - \frac{\overline{w} \cdot \overline{x}^+ + \overline{w} \cdot \overline{x}^-}{2} \end{split}\]

Nel nostro caso specifico troviamo quindi

\[\begin{split} \overline{w} &= 0.222 \cdot 1 \cdot (0, 3) + 0.889 \cdot 1 \cdot (1, 1) + 1.111 \cdot -1 \cdot (2, 2) \\ &= (-1,333, -0.667) \end{split}\]

Come possiamo vedere quindi, la retta che separa i punti è una combinazione lineare dei punti stessi.

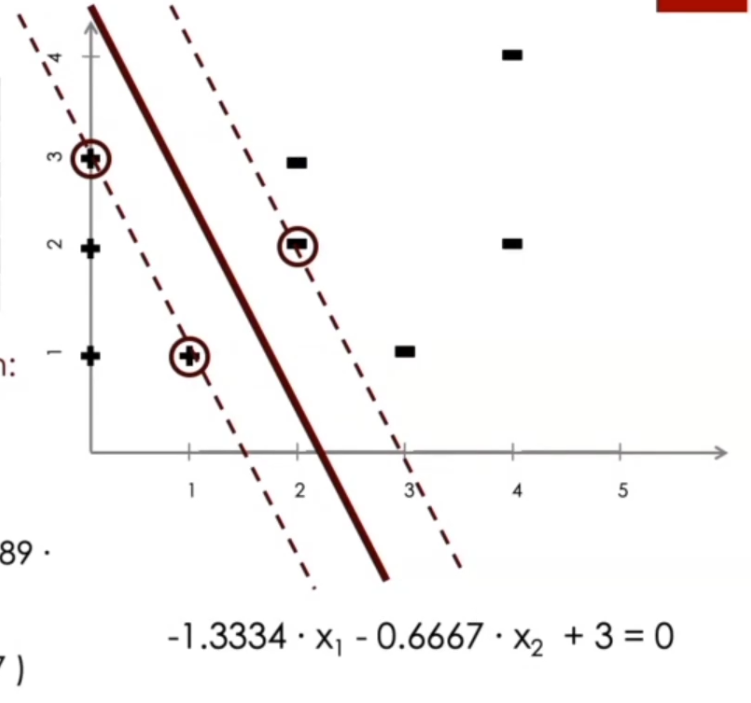
Una volta che abbiamo costruito la nostra retta, per classificare un nuovo punto \(\overline{x}_1\) ci basta calcolare \(\overline{w} \cdot \overline{x}_1 + b\) e vedere se è positivo o negativo.

Esistono due principali strategie per applicare un classificatore binario al caso multiclasse. Queste sono le seguenti:

1. One-Versus-All: Alleniamo tanti classificatori quanto sono le classi. Ogni classificatore è devoto a decidere se l'istanza appartiene o no alla particolare classe associata a quel classificatore. In questo schema in fase di addestramento l'importante è considerare, per ogni classificatore, come istanze positive solo le istanze appartenenti alle classe, e tutte le altre (che possono appartenere a classi diverse tra loro) sono considerare istanze negative. Una volta che si va a classificare si misura il margine rispetto a tutti gli iperpiani.

   Classificazione a mondo aperto vs a mondo chiuso: nel mondo chiuso tutto si riduce alle classe che prendo in considerazione. Quando rispondo ad una domanda di classificazione so per certo che l'istanza appartiene a una o più di queste tre classi, e quindi prendo la classe con il margine più vicino a \(0\), anche se tutti mi rispondono con un valore negativo. Se invece il mondo è aperto, il mio classificatore potrebbe anche non rispondere. In questo caso il classificatore può rispondere: "non lo conosco".

2. One-Versus-One: Metto in competizioni tutte le classi in una specie di torneo, costruendo per ogni coppia di classi un classificatore. In fase di classificazione rifaccio il torneo, classifico l'istanza su ogni classificatore, e scelgo la classe che ha vinto più scontri diretti.

Nel caso in cui abbiamo delle classi poco bilanciate, in caso di soft-SVM l'errore sarebbe principalmente pagato nella classe meno numerosa. Per cercare di diminuire questo problema è possibile spezzare la costante \(C\) in due costanti \(C_+\) e \(C_-\) in modo da aggiustare il contributo il costo dei falsi positivi e dei falsi negativi.

Così facendo il problema diventa

\[\begin{split} &\underset{}{\min} \,\,\, \frac12 \cdot ||w||^2 + C_+ \sum\limits_{i: y_i = 1} \xi_i + C_- \sum\limits_{j: y_j = -1} \xi_j\\ &\text{where } \\ & \;\;\;\; y_i(\overline{w} \cdot \overline{x} + b) \geq 1 - \xi_k \,\,,\,\,\, i = 1,\ldots,l \\ \end{split}\]

In questi casi il tuning viene fatto fissando il valore di una delle due costanti, e utilizziamo il rapporto tra i positivi e negativi per amplificare l'altro di conseguenza.