WMR 24 - Neural Networks I
Lecture Info
Date:
Course Site: Web Mining e Retrieval (a.a. 2019/20)
Lecturer: Roberto Basili.
Slides: ()
Table of Contents:
In questa lezione introduciamo i concetti di deep learning e neural networks.
1 Intro to Deep Learning
Il deep learning si è affermato come evoluzione della tradizionale teoria statistica dell'apprendimento, andando ad enfatizzare la capacità di aumentare l'espressività dei modelli attraverso l'utilizzo della profondità, ovvero attraverso l'utilizzo di un numero di neuroni sempre più grandi. Tramite il deep learning è quindi possibile imparare funzioni sempre più complesse andando ad aumentare il numero di parametri coinvolti nei modelli utilizzati.
Una caratteritica nell'avere così tanti parametri è che risulta estremamente difficile spiegare il "comportamento" della rete, ovvero è difficile capire perché ad un determinato input la rete a risposto in un determinato modo. Il problema della explainability è difficile da risolvere per le reti neurali in quanto l'architettura del modello è fortemente legata al calcolo numerico e quindi l'informazione viene dispersa in tantissime unità di elaborazioni.
Al contrario delle SVMs, nelle architetture di deep learning noi non siamo più interessati a legge lineari, ma siamo invece interessati a modelli altamente non lineari.
1.1 Types of Neural Networks
Nel corso della storia sono stati definite varie tipologie di reti neurali. Tra queste troviamo:
Multilayer Perceptrons: Evoluzione dei percettroni verso leggi non lineari.
Autoencoders.
Convolutional NNs.
Recurrent Neural Networks: Long Short Term Memories.
Attentive networks.
1.2 Dimensions of a Task
Ci sono tre dimensioni di problematicità per un dato task:
Complessità intrinseca del concetto da apprendere: predirre lo spam è probabilmente più semplice che tradurre in inglese.
Dati disponibili: Ho abbastanza dati per risolvere in modo supervised quel task?
Vincoli operativi: Posso permettermi di usare un determinato modello con un certo numero di parametri?
Più sono complessi i problemi, e più le reti neurali sono da favorire.
1.3 Symbols, Rules and Observations
Le reti neurali sono sistemi di intelligenza artificiale che invece che guardare a simboli e regole cercano di apprendere dai dati.
A physical symbol system has the necessity and sufficient means for general intelligent action.
Allen Newell & Herbert Simon
Symbols are Luminiferous Aether of AI.
Geoff Hinton
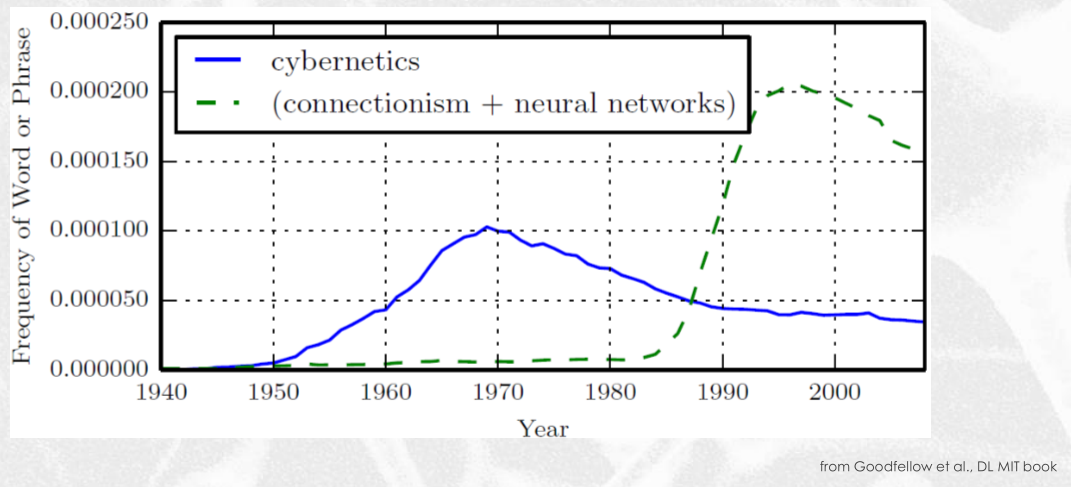
1.4 Connectionism and Deep Learning
Il seguente grafico mostra la frequenza di determinate parole nel corso degli anni.
1.5 What we want
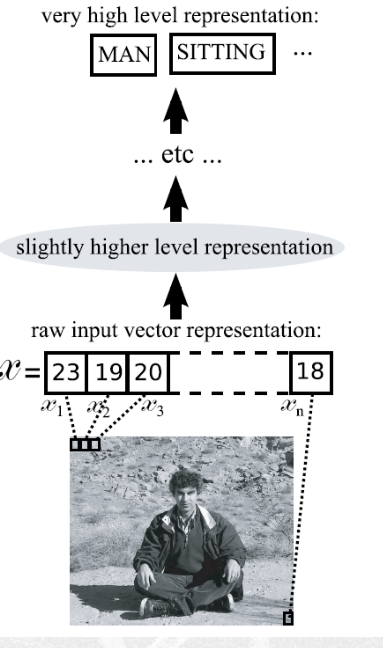
Noi vogliamo costruire dei sistemi che ci permettano di costruire delle rappresentazioni altamente astratte a partire da determinati raw data, come ad esempio delle immagini.
1.6 History
2 Vector Spaces, Functions and Learning
Come avevamo menzionato parlando della PAC-learnability, noi apprendiamo muovendoci tra ipotesi più specifiche e ipotesi più generali.
Le reti neurali fanno la stessa cosa. In particolare il nostro obiettivo è quello di interpolare la funzione ottima \(f^*(x)\) che associa ad ogni vettore delle feature dell'istanza presa in considerazione la classe desiderata. L'idea quindi è quella di approssimare la funzione ideale con una funzione \(h(x)\) che appartiene alla famiglia delle funzioni \(g(x; \theta)\) parametrizzata in \(\theta\) in modo tale da avere che
\[\forall x \in L: h(x) \approx f^*(x)\]
dove \(L\) è il learning set.
Avevamo poi visto che per i modelli a complessità bassa la macchina non ci consente di variare molto il suo comportamento. Detto questo, abbiamo anche una varianza bassa, e quindi l'errore che effettuiamo nel training set sarà molto vicino a quello effettuato nel test sample.
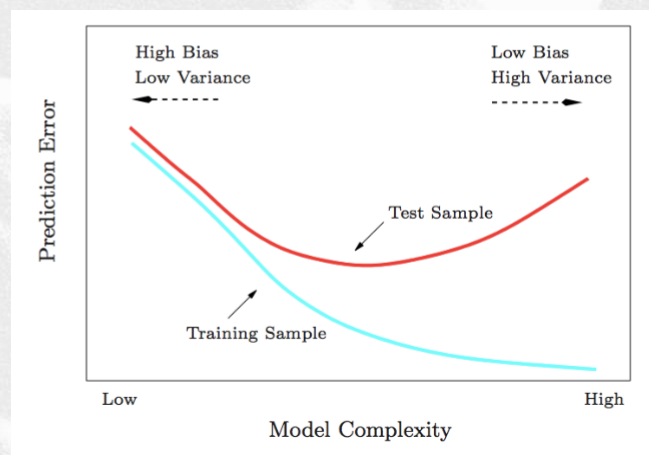
Al crescere della complessità invece abbiamo una grande capacità di adattare il nostro modello alla funzione desiderata, ma così facendo aumentiamo anche la varianza.
I modelli lineari sono quei modelli in cui le features sono combinate tra loro linearmente per ottenere la funzione \(h(x)\). In particolare
\[h(\overline{x}) = g\Big( \sum\limits_n \theta_n x_n + b \Big)\]
Il percettrone è leggermente più generale di una legge lineare, in quanto non è sempre utilizzata per separare linearmente i dati (come nel caso delle SVMs), e può essere descritto nel seguente modo
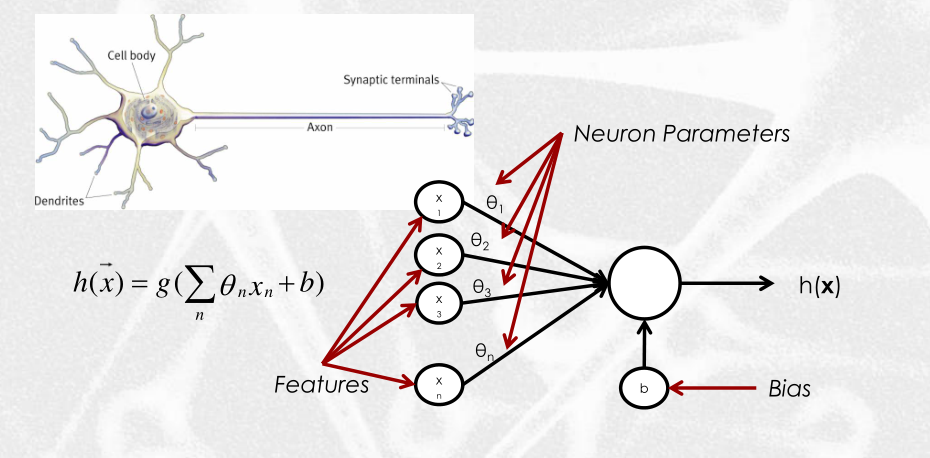
2.1 On Representation
Nelle SVM avevamo visto che tramite il kernel era possibile cambiare la rappresentazione dei nuovi dati, andandoli a mappare in un feature space in cui i dati diventavano linearmente separabili.
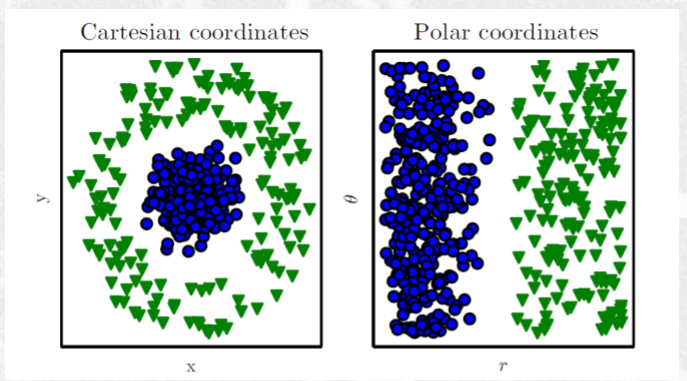
Fino a questo punto però il particolare kernel utilizzato era scelto dal programmatore e codificato nel processo di training del modello.
Tramite le reti neurali siamo invece in grado di tirare fuori durante l'addrestramento, non solo i parametri del modello finale, ma anche la rappresentazione ottima, dove l'ottimalità dipende come al solito dal problema.
La capacità di costruire una rappresentazione ottima si chiama encoding. L'encoding è una delle funzioni delle reti neurali.
2.2 The Role of Depth
I neuroni sono poi organizzati a strati, e i neuroni di ciascun strato possono interagire con i neuroni degli stati successivi mandandoli dei segnali.
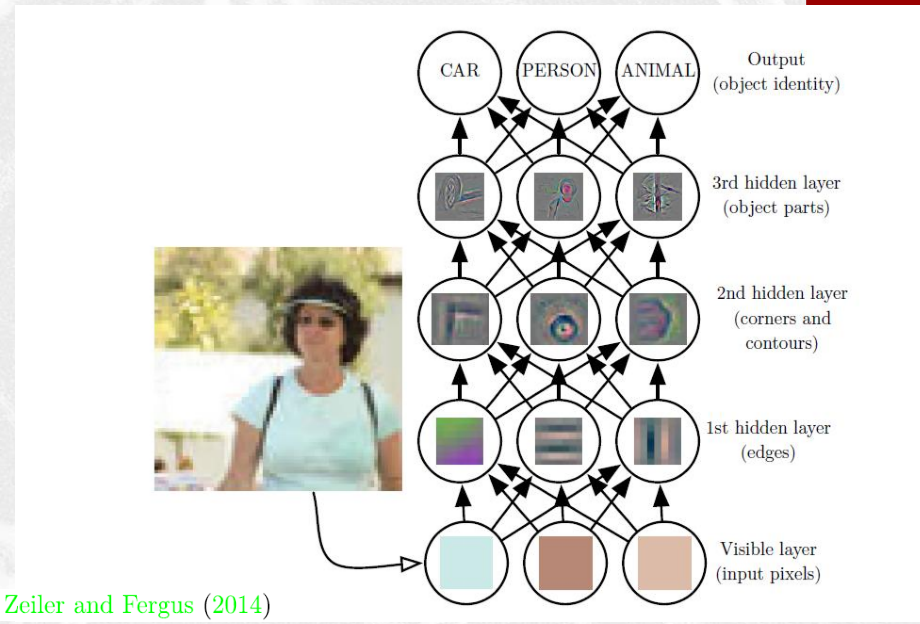
Come possiamo vedere le reti neurali fanno quindi due cose:
Apprendono a decidere.
Apprendono le rappresentazioni.
3 Multilayer Perceptron
Quando abbiamo un semplice neurone la legge \(h\) è ottenuta applicando una funzione di attivazione \(g\) (eventualmente non lineare) ad una combinazione lineare delle features pesate
\[h(\overline{x}) = g(\overline{x} ; \overline{\theta}, b) = g\Big(\sum\limits_n \theta_n x_n + b \Big)\]
Se noi poi aumentiamo la capacità di un singolo percettrone andando ad aggiungere neuroni a strati otteniamo un percettrone a due layers
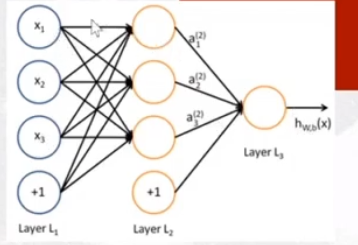
In questo modo quindi abbiamo delle funzioni aggiunive \(g^{(1)}, g^{(2)}, \ldots, g^{(k)}\) che danno luogo alla seguente funzione
\[\begin{split} h(\overline{x}) &= g^{(2)}\Big(g^{(1)}(\overline{x}, \overline{\theta}^{(1)}, b^{(1)}); \overline{\theta}^{(2)}, b^{(2)}\Big) \\ &= g^{(2)} \Big(W^{(2)}\Big(g^{(1)}\Big(W^{(1)} \overline{x} + b^{(1)} \Big) \Big) + b^{(2)} \Big) \\ \end{split}\]
dove \(W^{(1)}\) è una matrice \(3 \times 3\) e \(W^{(2)}\) è una matrice \(3 \times 1\).
Iterando questo procedimendo posso aggiungere layers su layers.
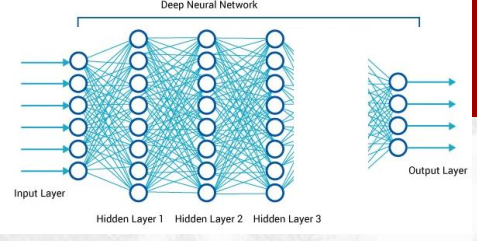
In formula,
\[h(\overline{x}) = g^{(k)} \Big( W^{(k)} g^{(k-1)}(W^{(k-1)} \ldots g^{(1)}(W^{(1)} \cdot \overline{x} + b^{(1)}) \ldots + b^{(k-1)}) + b^{(k)} \Big)\]
4 Neural Networks
Data una rete neurale, abbiamo che
\(n_l\) è il number of layers, ovvero il numero di layers.
\(s_l\) invece determina il numero di unità nel primo layer.
Il layer \(l\) è denotato \(L_l\).
Il layer \(l\) e il layer \(l+1\) sono connessi tramite una matrice \(W^{(l)}\) di parametri, in cui \(W^{(l)}_{i, j}\) connette l' \(i\) esimo neurone dello strato successivo al \(j\) esimo neurone dello stato precedente.
\(b^{(l)}_i\) è il bias associato al neurone \(i\) nel layer \(l+1\).
4.1 Single Neuron View
Fondamentalmente quindi quello che fa un singolo neurone è un'operazione di regressione.
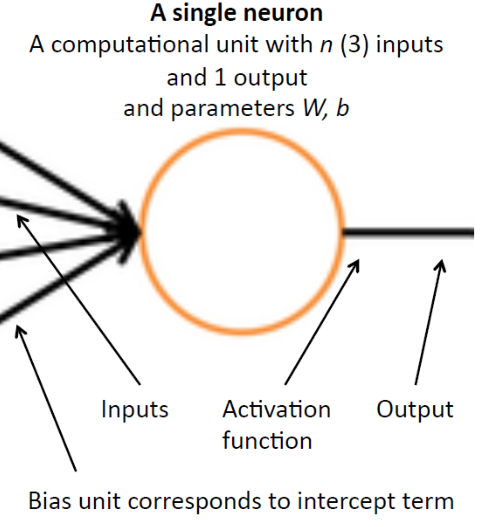
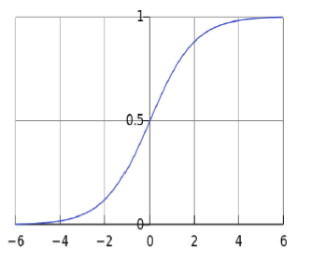
4.2 Sigmoid
Una delle funzioni non lineari monotona crescente che ci piace come \(g()\) è la seguente
\[f(z) = \frac{1}{1 + e^{-z}}\]
Al crescere di \(z\) la funzione tende a \(1\) e viceversa al decrescere di \(z\) al funzione tende a \(0\).