Support Vector Machine

Supponiamo di avere un iperpiano di separazione \((\mathbf{w}^T, w_0)\) per un dato training set \(D\), e consideriamo un elemento \((x_i, y_i) \in D\) di tale training set.

---

Def: Il margine funzionale dell'elemento \((x_i, y_i)\) rispetto all'iperpiano \((\mathbf{w}^T, w_0)\) è definito nel seguente modo

\[\overline{\gamma_i} = y_i \cdot (\mathbf{w}^T \mathbf{x} + w_0)\]

---

Intuitivamente possiamo pensare al margine funzionale come ad una misura della confidenza che abbiamo nella nostra classificazione. In particolare abbiamo che se \(\overline{\gamma}_i > 0\), allora la predizione effettuata dal modello sul training example \((x_i, y_i)\) è corretta. Infatti vale \(\overline{\gamma}_i > 0\) solo quando \(y_i\) e \(\mathbf{w}^T \mathbf{x} + w_0\) hanno lo stesso segno, ovvero solo quando l'iperpiano mette \(x_i\) nella sua classe di appartenenza.

Inoltre, se \(y_i = 1\), per avere un alto margine funzionale, ovvero per avere un'alta confidenza nella nostra classificazione, dobbiamo avere un grande valore di \(\mathbf{w}^T \mathbf{x} + w_0\), quantità proporzionale (non uguale!) alla distanza di \(\mathbf{x}\) dall'iperpiano di separazione. Lo stesso ragionamento vale per il caso \(y_i = -1\). Questo intuitivamente ha molto senso: più lontano il punto si trova dall'iperpiano di separazione, e più siamo sicuri di averlo classificato bene.

A partire dai margini funzionali dei vari elementi del training set possiamo poi definire il margine funzionale rispetto all'intero training set.

---

Def: Fissato il training set \(D = \{(x_1, y_1), \ldots, (x_n, y_n)\}\) e l'iperpiano di separazione \((\mathbf{w}^T, w_0)\), il margine funzionale del training set rispetto all'iperpiano è definito come il minimo margine funzionale rispetto ai vari elementi del training set. In formula,

\[\overline{\gamma} = \underset{i}{\min} \overline{\gamma_i}\]

---

L'unica proprietà del margine funzionale che lo rende problematico da utilizzare per misurare la qualità di un iperpiano di separazione è il fatto che il margine funzionale rispetto ai singoli elementi (e dunque rispetto al training set), varia allo scalare dei parametri dell'iperpiano.

In particolare, se \(\overline{\gamma}\) è il margine funzionale rispetto all'iperpiano \((\mathbf{w}, w_0)\), andando a scalare i parametri dell'iperpiano per una costante \(2\) otteniamo un nuovo iperpiano \((2 \mathbf{w}, 2 w_0)\). Ora, mentre la classificazione dei vari punti in questo nuovo iperpiano non è assolutamente cambiata, in quanto

\[\text{sign}(\mathbf{w}^T \mathbf{x} + w_0) = \text{sign}(2 \mathbf{w}^T \mathbf{x} + 2 w_0)\]

notiamo che invece il margine funzionale è cambiato, in quanto il nuovo margine funzionale rispetto all'elemento \((\mathbf{x}_i, y_i)\) è diventato

\[\begin{split} \overline{\gamma}_{\text{new}} &= y_i (2 \mathbf{w}^T \mathbf{x}_i + 2w_0) \\ &= 2 \cdot y_i (\mathbf{w}^T \mathbf{x}_i + w_0) \\ &= 2 \cdot \overline{\gamma}_{\text{old}} \end{split}\]

Questo significa che semplicemente scalando i parametri del nostro iperpiano siamo in grado di rendere il margine funzionale rispetto ai vari elementi (e dunque rispetto al training set), arbitrariamente grande. Dunque, non è possibile utilizzare il margine funzionale, almeno per come è stato definito, per misurare la qualità di un iperpiano di separazione.

Per avere una quantità più robusta con cui misurare la qualità dei nostri iperpiani consideriamo la seguente figura

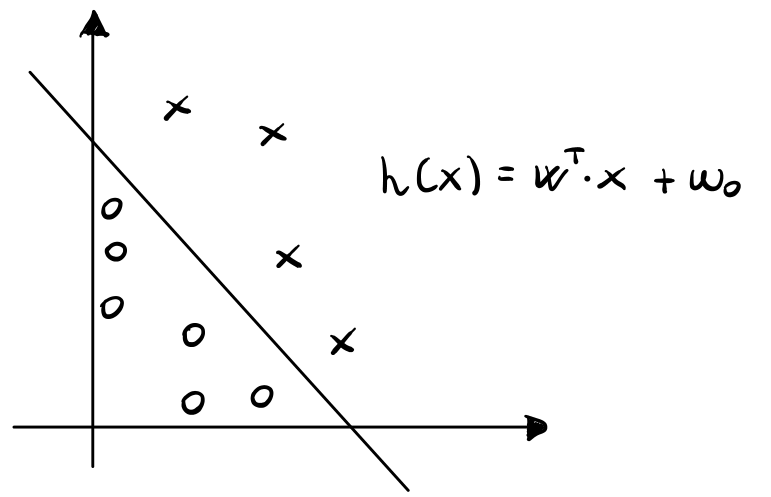
e notiamo il seguente fatto geometrico: il vettore dei parametri \(\mathbf{w}\) dell'iperpiano è ortogonale all'iperpiano.

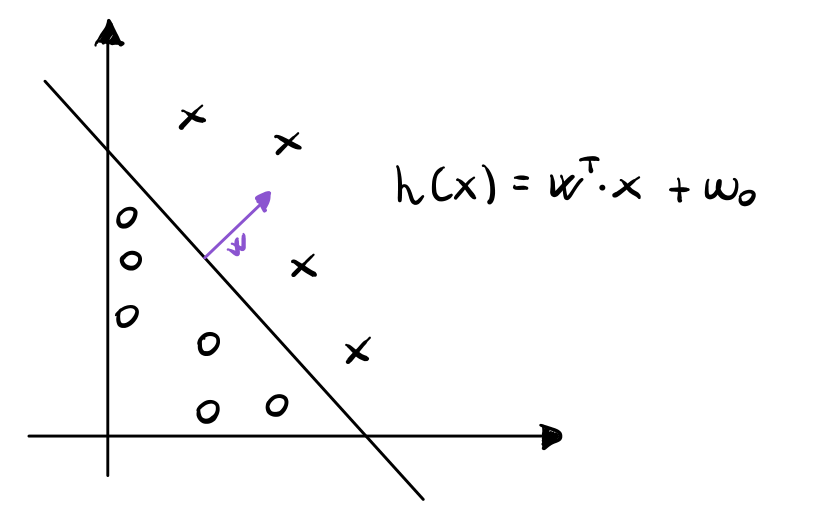
A questo punto consideriamo un punto \(\mathbf{x}_i\) classificato come positivo (nel grafico i punti classificati come positivi sono le X, mentre quelli negativi sono le O), e consideriamo in particolare la distanza tra il punto e l'iperpiano di separazione, che indicheremo con \(d_i\).

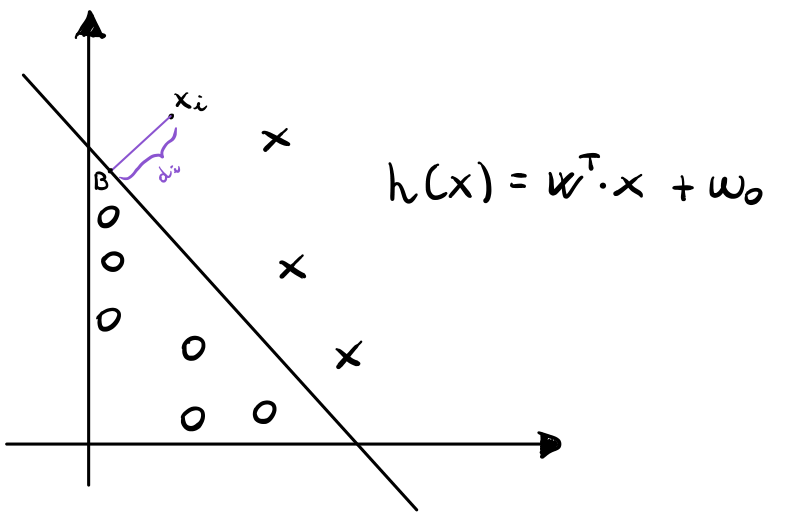
Per calcolare \(d_i\) ci basta notare che \(\mathbf{w}/||\mathbf{w}||\) è un vettore di lunghezza unitaria che punta nella stessa direzione di \(\mathbf{w}\), che per quanto detto prima è ortogonale all'iperpiano. Da questo segue che il punto \(B\) è dato dal seguente vettore

\[\mathbf{x}_i - \frac{\mathbf{w}}{||\mathbf{w}||} \cdot d_i\]

Dato poi che il punto \(B\) soddisfa l'equazione dell'iperpiano, otteniamo che

\[\mathbf{w}^T \Bigg(\mathbf{x}_i - \frac{\mathbf{w}}{||\mathbf{w}||} \cdot d_i \Bigg) + w_0 = 0\]

risolvendo per \(d_i\) troviamo

\[d_i = \frac{\mathbf{w}^T \mathbf{x}_i + w_0}{||\mathbf{w}||} = \Bigg(\frac{\mathbf{w}}{||\mathbf{w}||} \Bigg)^T \mathbf{x}_i + \frac{w_0}{||\mathbf{w}||}\]

In modo più diretto per calcolare \(d_i\) potevamo semplicemente utilizzare la seguente formula, che calcola la distanza tra un punto \(\mathbf{x}\) e un iperpiano \((\mathbf{w}, w_0)\)

\[\text{Distance} = \frac{|\mathbf{w} \mathbf{x} + w_0|}{||w||}\]

---

Siamo quindi pronti per introdurre la definizione di interesse

Def: Il margine geometrico dell'elemento \((x_i, y_i)\) rispetto all'iperpiano \((\mathbf{w}, w_0)\) è definito come segue

\[\gamma_i = y_i \Bigg( \Big(\frac{\mathbf{w}}{||\mathbf{w}||}\Big)^T \mathbf{x}_i + \frac{w_0}{||\mathbf{w}||} \Bigg)\]

Come è possibile vedere, il margine geometrico codifica due informazioni diverse:

• La distanza dell'elemento in questione dall'iperpiano (il valore assoluto del margine).

• Se la classificazione è avvenuta bene o male (il segno del margine).

Come poi abbiamo fatto nel caso dei margini funzionali, anche per i margini geometrici possiamo estendere questa definizione all'intero dataset di training.

Def: Fissato il training set \(D = \{(x_1, y_1), \ldots, (x_n, y_n)\}\) e l'iperpiano di separazione \((\mathbf{w}^T, w_0)\), il margine geometrico del training set rispetto all'iperpiano è definito come il minimo margine geometrico dei vari elementi del training set rispetto all'iperpiano. In formula,

\[\gamma = \underset{i}{\min} \gamma_i\]

---

Il margine geometrico può essere visto come una specie di normalizzazione del margine funzionale. Infatti, margine geometrico e margine funzionale sono relazionati tra loro come segue

\[\gamma = \frac{\overline{\gamma}}{||\mathbf{w}||}\]

Da questo segue che quando \(||\mathbf{w}|| = 1\), allora i concetti di margine funzionale e margine geometrico corrispondono tra loro. In generale però la problematica che avevamo riscontrato con i margini funzionali — ovvero il fatto che scalando i parametri del modello per una costante riuscivamo ad aumentare arbitrariamente tanto anche il margine funzionale dell'iperpiano rispetto al training set — non vale più rispetto ai margini geometrici.

Infatti, considerando un iperpiano di partenza \((\mathbf{w}, w_0)\) ed un esempio \((x_i, y_i)\), e fissata \(c\) una costante arbitraria, troviamo che

• Nel vecchio modello, il margine geometrico di \(x_i\) rispetto all'iperpiano \((\mathbf{w}, w_0)\) è dato da

  \[\gamma_i^{\text{old}} = \Bigg( \Big(\frac{\mathbf{w}}{||\mathbf{w}||}\Big)^T \mathbf{x}_i + \frac{w_0}{||\mathbf{w}||} \Bigg)\]

• Nel nuovo modello, quello ottenuto scalando i parametri di \(c\), ovvero \((c \mathbf{w}, cw_0)\), il margine geometrico è dato da

  \[\begin{split} \gamma_i^{\text{new}} &= \Bigg( \Big(\frac{\mathbf{c w}}{||\mathbf{c w}||}\Big)^T \mathbf{x}_i + \frac{c w_0}{||\mathbf{c w}||} \Bigg) \\ &= \Bigg( \Big(\frac{\mathbf{w}}{||\mathbf{w}||}\Big)^T \mathbf{x}_i + \frac{w_0}{||\mathbf{w}||} \Bigg) \\ &= \gamma_i^{\text{old}} \end{split}\]

L'idea è quindi quella di utilizzare il margine geometrico per misurare la qualità di separazione di un iperpiano. In particolare, più grande è il margine geometrico di un training set, e più l'iperpiano considerato riesce a separare le due classi del training set tra loro.

L'iperpiano che massimizza il margine geometrico è detto maximum margin separating hyperplane.

L'idea alla base di una SVM è proprio quella di trovare l'iperpiano che massimizza il margine geometrico rispetto al training set \(D\). Per fare questo si imposterà un problema di ottimizzazione. L'impostazione del problema può essere fatta in due modi diversi:

• Se si assume che i dati sono linearmente separabili, allora troviamo le HARD-SVMs che separano i dati del training set senza nessun errore di classificazione.

• Se invece non si assume nulla rispetto ai dati in termini di separabilità lineare, il problema di ottimizzazione viene rilassato, e troviamo le SOFT-SVMs, che durante la classificazione del training set possono eventualmente fare degli errori.

Come abbiamo già detto, le SVM cercano di trovare l'iperpiano di separazione che massimizza il margine geometrico. Addestrare una SVM significa quindi risolvere il seguente problema di ottimizzazione

---

\[\begin{split} & \;\;\;\;\;\;\;\;\; \underset{\overline{\gamma}, \mathbf{w}, w_0}{\max} \overline{\gamma} \\ \text{such that,}& \\ & y_i (\mathbf{w}^T \mathbf{x}_i + w_0) \geq \overline{\gamma} \;\;\;,\;\;\; i = 1,\ldots,n \\ & ||\mathbf{w}|| = 1 \\ \end{split}\]

---

Come già detto, quando \(||\mathbf{w}|| = 1\) abbiamo che margine geometrico e margine funzionale combaciano. Dunque, andando a massimizzare il margine funzinale del training set sotto questi vincoli, massimizziamo anche quello geometrico.

Il problema della formulazione appena data però è il fatto che il vincolo \(|| \mathbf{w}|| = 1\) non è un vincolo convesso, e dunque questo problema di ottimizzazione, per come è stato formulato, non può essere risolto da tecniche standard note.

Per cercare di riportare il problema ad una forma più gestibile quindi riportiamo la seguente riformulazione

---

\[\begin{split} & \;\;\;\;\;\;\;\;\; \underset{\overline{\gamma}, \mathbf{w}, w_0}{\max} \frac{\overline{\gamma}}{||\mathbf{w}||} \\ \text{such that,}& \\ & y_i (\mathbf{w}^T \mathbf{x}_i + w_0) \geq \overline{\gamma} \;\;\;,\;\;\; i = 1,\ldots,n \\ \end{split}\]

---

Dato che margine geometrico \((\gamma)\) margine funzionale sono \((\overline{\gamma})\) sono relazionati tra loro come \(\gamma = \overline{\gamma} /||\mathbf{w}||\), risolvendo questo problema andiamo comunque a trovare l'iperpiano che massimizza il margine geometrico.

Il problema di quest'altra formulazione è che adesso è la funzione ad essere problematica.

Continuando, per trasformare ulteriormente il problema utilizziamo il fatto che possiamo introdurre una costante di scalatura \(c\) nei parametri del modello, senza così facendo modificare il margine geometrico. In particolare scaliamo i parametri dell'iperpiano per imporre che il margine funzionale rispetto al training set sia \(1\), ovvero imponiamo la condizione

\[\overline{\gamma} = 1\]

Sostituendo nella formulazione precedente troviamo quindi il seguente problema

---

\[\begin{split} & \;\;\;\;\;\;\;\;\; \underset{\mathbf{w}, w_0}{\max} \frac{1}{||\mathbf{w}||} \\ \text{such that,}& \\ & y_i (\mathbf{w}^T \mathbf{x}_i + w_0) \geq 1 \;\;\;,\;\;\; i = 1,\ldots,n \\ \end{split}\]

---

Infine, notando che massimizzare \(1/||\mathbf{w}||\) equivale a minimizzare \(1/2 \cdot ||\mathbf{w}||^2\) arriviamo al seguente problema

---

\[\begin{split} & \;\;\;\;\;\;\;\;\; \underset{\mathbf{w}, w_0}{\min} \frac{1}{2} ||\mathbf{w}||^2 \\ \text{such that,}& \\ & y_i (\mathbf{w}^T \mathbf{x}_i + w_0) \geq 1 \;\;\;,\;\;\; i = 1,\ldots,n \\ \end{split}\]

---

Finalmente, quest'ultima forma del problema può essere risolta in modo efficiente in quanto contiene una funzione obiettivo convessa e quadratica e dei vincoli lineari.

A questo punto una possibile strada potrebbe essere quella di risolvere questo problema e fermarci qui. Noi però non seguiremo questa strada, in quanto risulterà molto utile applicare la teoria dei moltiplicatori di Lagrange, discussa alla fine del seguente documento, al fine di arrivare alla formulazione duale del problema.

Per applicare il lagrangiano espriamo i vincoli del problema di ottimizzazione trovato, ovvero

\[\begin{split} & \;\;\;\;\;\;\;\;\; \underset{\mathbf{w}, w_0}{\min} \frac{1}{2} ||\mathbf{w}||^2 \\ \text{such that,}& \\ & y_i (\mathbf{w}^T \mathbf{x}_i + w_0) \geq 1 \;\;\;,\;\;\; i = 1,\ldots,n \\ \end{split}\]

come dei vincoli della forma \(g_i(x) \leq 0\). Per fare questo ci basta imporre per ogni \(i\)

\[g_i(\mathbf{w}, w_0) := -y_i(\mathbf{w}^T \mathbf{x}_i + w_0) + 1\]

notiamo che per ogni elemento del training set abbiamo un determinato vincolo.

---

Dato che non abbiamo vincoli di uguaglianza \(h_i(x) = 0\), il lagrangiano del problema di ottimizzazione appena posto è il seguente

\[\begin{split} \mathcal{L}(\mathbf{w}, w_0, \alpha) &= \frac{1}{2} || \mathbf{w} ||^2 + \sum\limits_{i = 1}^n \alpha_i \cdot g_i(\mathbf{w}, w_0) \\ &= \frac{1}{2} || \mathbf{w} ||^2 + \sum\limits_{i = 1}^n \alpha_i \cdot \Big( y_i (\mathbf{w}^T \mathbf{x}_i + w_0) - 1 \Big) \\ \end{split}\]

Per passare alla forma duale, che è la seguente

\[\underset{\alpha: \alpha_i > 0}{\max} \underset{\mathbf{w}, w_0}{\min} \mathcal{L}(\mathbf{w}, w_0, \alpha)\]

dobbiamo minimizzare \(\mathcal{L}(\mathbf{w}, w_0, \alpha)\) rispetto a \(\mathbf{w}\) e \(w_0\).

• Per quanto riguarda \(\mathbf{w}\), andandoci a calcolare la derivata parziale rispetto a \(w_i\) e settandola uguale a \(0\) troviamo

  \[\begin{split} \frac{\partial \mathcal{L}(\mathbf{w}, w_0, \alpha)}{\partial w_i} &= \frac{\partial}{\partial w_i} \frac12 \cdot \sum\limits_{j = 1}^k w_j^2 - \sum\limits_{j = 1}^n \Big(\alpha_i y_i \sum_{h = 1}^k w_h x_{i,h} + \alpha_i y_i w_0 - \alpha_i\Big) \\ &= \Big(w_i - \sum\limits_{h = 1}^n \alpha_h y_h x_{i,h}\Big)_{i = 1, \ldots, n} = 0 \\ \end{split}\]

  e quindi impostando il gradiente rispetto a \(\mathbf{w}\) uguale a \(0\) troviamo

  \[\mathbf{w} - \sum\limits_{i = 1}^n \alpha_i y_i \mathbf{x}_i = 0\]

  il che equivale a dire

  \[\mathbf{w} = \sum\limits_{i = 1}^n \alpha_i y_i \mathbf{x}_i\]

  ---

• Invece per quanto riguarda \(w_0\) troviamo

  \[\frac{\partial \mathcal{L}(\mathbf{w}, w_0, \alpha)}{\partial w_0} = \sum\limits_{i = 1}^n \alpha_i y_i = 0\]

---

Sostituendo nel lagrangiano, troviamo la seguente formulazione

\[\mathcal{L}(\mathbf{w}, w_0, \alpha) = \sum\limits_{i = 1}^n \alpha_i - \frac12 \sum\limits_{i, j = 1}^n y_i y_j \alpha_i \alpha_j (\mathbf{x}_i)^T \mathbf{x}_j\]

e il problema di ottimizzazione duale è quindi

---

\[\begin{split} & \;\;\;\;\;\;\;\;\; \underset{\alpha}{\max} \sum\limits_{i = 1}^n \alpha_i - \frac12 \sum\limits_{i, j = 1}^n y_i y_j \alpha_i \alpha_j (\mathbf{x}_i)^T \mathbf{x}_j \\ \text{such that,}& \\ & \alpha_i \geq 0 \\ & \sum\limits_{i = 1}^n \alpha_i y_i = 0 \\ \end{split}\]

---

Per risolvere il problema duale è possibile utilizzare l'algoritmo SMO, che sta per sequential minimal optimization, trovato da John Platt.

Dato che per il nostro problema valgono sia le condizioni che collegano il problema duale a quello primale e sia le KKT conditions, abbiamo che risolvendo il duale siamo anche in grado di risolvere il primale.

Supponiamo quindi di aver risolto il problema duale e di aver trovato i coefficienti ottimali \(\alpha_i^*\), \(i = 1,\ldots,n\).

Per passare dalla soluzione del duale alla soluzione del primale, possiamo utilizzare le seguenti equazioni:

• Per quanto riguarda \(\mathbf{w}\) troviamo

  \[\begin{split} \mathbf{w}^* &= \sum\limits_{i = 1}^n \alpha_i^* y_i \mathbf{x}_i \\ \\ w_i^* &= \sum\limits_{j = 1}^n \alpha_j^* y_j (\mathbf{x}_j)_i \\ \end{split}\]

• Per il termine noto \(w_0\) invece lo possiamo calcolare come segue

  \[w_0^* = - \frac{\underset{i: y_i = -1}{\max} (\mathbf{w}^*)^T \mathbf{x}_i + \underset{i: y_i = 1}{\min} (\mathbf{w}^*)^T \mathbf{x}_i}{2}\]

Notiamo che il problema primale che avevamo trovato avevamo i seguenti vincoli

\[y_i(\mathbf{w}^T \mathbf{x}_i + w_0) \geq 1 \;\;\;,\;\;\, i = 1,\ldots n\]

a seconda della soluzione che troviamo per determinati punti \(\mathbf{x}_i\) tale vincolo sarà rispettato con l'uguaglianza, ovvero tale che

\[y_i(\mathbf{w}^T \mathbf{x}_i + w_0) = 1\]

I punti per cui l'equazione precedente è vera sono chiamati support vectors. Questi punti sono di fondamentale importanza, in quanto, come vedremo, sono gli unici punti da considerare quando dobbiamo classificare un nuovo punto. Sia \(\mathcal{S}\) l'insieme degli indici associati ai vettori di supporto

\[\mathcal{S} = \{i \in \{1, ..., n\}: \;\;\, y_i(\mathbf{w}^T \mathbf{x}_i + w_0) = 1\}\]

Rispetto alla formulazione duale del problema, i vettori di supporto sono i vettori associati ai coefficienti di lagrange non-nulli. Infatti, dalle KTT conditions (che, come abbiamo già menzionato, valgono per il nostro particolare problema), sappiamo che vale la seguente equazione

\[\alpha_i^* \cdot g_i(\mathbf{w}^*, w_0) = 0 \;\;,\;\; i = 1,\ldots,n\] dunque quando

\[g_i(\mathbf{w}^*, w_0) < 0 \iff y_i((\mathbf{w}^*)^T \mathbf{x}_i + w_0) > 1\]

necessariamente deve valere \(\alpha_i^* = 0\). E quindi se abbiamo che \(\alpha_i^* > 0\), allora necessariamente dobbiamo avere che

\[g_i(\mathbf{w}^*, w_0) = 0 \iff y_i((\mathbf{w}^*)^T \mathbf{x}_i + w_0) = 1\]

Questo significa che se \(\alpha_i^* > 0\), allora possiamo concludere che l'elemento \(\mathbf{x}_i\) è un vettore di supporto, ovvero che \(\mathbf{x}_i \in \mathcal{S}\).

Supponiamo adesso di aver addestrato la nostra SVM. Ovvero, supponiamo di aver risolto il problema duale all'ottimo, di aver ottenuto i coefficienti di lagrange ottimi \(\alpha_i^*\), e di esserci calcolati anche la soluzione ottima per il problema primale \((\mathbf{w}^*, w_0^*)\), che rappresenta proprio l'iperpiano che massimizza il margine geometrico.

Come facciamo adesso a classificare un nuovo punto \(x \in \chi\)?

L'idea è che abbiamo due linguaggi diversi per esprimere la classificazione, ciascuno legato ad una particolare formulazione del problema:

• Rispetto al problema primale, possiamo classificare il nuovo punto \(x\) utilizzando i parametri dell'iperpiano ottimale trovato \((\mathbf{w}^*, w_0^*)\) e calcolando la solita funzione segno.

  \[y(\mathbf{x})) = \text{sign}((\mathbf{w}^*)^T \mathbf{x} + w_0^*) = \begin{cases} 1 &,\;\; (\mathbf{w}^*)^T \mathbf{x} + w_0^* \geq 0 \\ -1 &,\;\; (\mathbf{w}^*)^T \mathbf{x} + w_0^* < 0 \\ \end{cases}\]

• Altrimenti possiamo calcolare il segno a partire dalla formulazione duale del problema.

  \[y(\mathbf{x}) = \text{sign}\Bigg(\sum\limits_{i = 1}^n \alpha_i^* y_i \mathbf{x}_i \mathbf{x} + w_0 \Bigg)\]

Notiamo infatti che da come sono relazionati i coefficienti ottimali dei due problemi, abbiamo che

\[(\mathbf{w}^*)^T \mathbf{x} + w_0^* = \sum\limits_{i = 1}^n \alpha_i^* y_i \mathbf{x}_i \mathbf{x} + w_0^*\]

Anche se le due formulazioni sembrano abbastanza simili, ci sono due importanti osservazioni da fare rispetto alla seconda formulazione:

1. Nella seconda formulazione la classificazione viene effettuata andando a calcolare il prodotto scalare dell'elemento da classificare con gli altri elementi del training set. In altre parole, la classificazione è ottenuta come una combinazione lineare dei dati di training.

2. Inoltre, nella pratica, la formulazione duale è tipicamente più efficiente di quella primale. Questo segue dal fatto che dobbiamo considerare solamente gli elementi del training set associati a moltiplicatori di Lagrange \(\alpha_i^* > 0\), ovvero solamente ai support vectors. Dato che tipicamente \(|\mathcal{S}| << n\), la seconda formulazione necessita di fare meno calcoli.

Riassumendo, una volta ottenuti i moltiplicato di Lagrange ottimi \(\alpha_i^*\), possiamo classificare un nuovo punto \(\mathbf{x}\) come segue

\[y(\mathbf{x}) = \text{sign}\Bigg(\sum\limits_{i \in \mathcal{S}} \alpha_i^* y_i \mathbf{x}_i \mathbf{x} + w_0 \Bigg)\]

dove \(\mathcal{S}\) è l'insieme degli indici associati ai vettori di supporto.

Consideriamo la versione HARD del problema di ottimizzazione visto prima per il caso linearmente separaible

\[\begin{split} & \;\;\;\;\;\;\;\;\; \underset{\mathbf{w}, w_0}{\min} \frac{1}{2} ||\mathbf{w}||^2 \\ \text{such that,}& \\ & y_i (\mathbf{w}^T \mathbf{x}_i + w_0) \geq 1 \;\;\;,\;\;\; i = 1,\ldots,n \\ \end{split}\]

Per rilassare il problema l'idea è quella di introdurre delle slack variables \(\xi_i\) e di rilassare il vincolo sui margini funzionali richiedendo che il margine funzionale non sia più necessariamente maggiore o uguale ad \(1\). In particolare troviamo i seguenti vincoli per ogni \(i = 1,\ldots,n\)

\[\begin{split} \xi_i &\geq 0 \\ y_i(\mathbf{w}^T \mathbf{x} + b) &\geq 1 - \xi_i \\ \end{split}\]

Per cercare però di limitare il modo in cui utilizziamo queste slack variables, l'idea è di modificare anche la funzione obiettivo da minimizzare, introducendo un parametro di regolarizzazione in funzione degli \(x_i\). In particolare la nuova funzione diventa

\[\underset{\xi_i, \mathbf{w}, w_0}{\min} \frac{1}{2} || \mathbf{w} ||^2 + C \cdot \sum\limits_{i = 1}^n \xi_i\]

dove il parametro \(C\) regola l'effetto delle slack variables sul costo finale: più piccolo è \(C\) e meno effetto avranno gli errori sul valore della funzione, mentre più grande è \(C\) e più effetto avranno gli errori sul valore della funzione.

In modo analogo a quanto fatto prima (senza però riportare i singoli steps), possiamo costruire, a partire dal Lagrangiano, il relativo problema duale

\[\begin{split} & \underset{\alpha}{\max} \sum\limits_{i = 1}^n \alpha_i - \frac12 \sum\limits_{i, j = 1}^n y_i y_j \alpha_i \alpha_j (\mathbf{x}_i)^T \mathbf{x}_j \\ \text{such that,}& \\ & 0 \leq \alpha_i \leq C \\ & \sum\limits_{i = 1}^n \alpha_i y_i = 0 \\ \end{split}\]

Come è possibile vedere, la forma del problema non cambia molto, l'unica cosa che cambia sono i vincoli imposti alle \(\alpha_i\): adesso sono anche limitate superiormente da \(C\).

---

Una volta che abbiamo risolto il problema duale, possiamo applicare il classificatore esattamente come prima.

Introduciamo la seguente funzione, che prende il nome di generalized Lagrangian

\[\mathcal{L}(x, \alpha, \beta) = f(x) + \sum\limits_{i = 1}^n \alpha_i g_i(x) + \sum\limits_{j = 1}^m \beta h_i(x)\]

dove i valori \(\alpha_i\) e \(\beta_i\) sono detti Lagrange multipliers (moltiplicatori di Lagrange).

A questo punto possiamo riformulare il problema originale, quello che abbiamo chiamato problema "primale", introducendo il seguente problema

\[\theta_{\mathcal{P}}(x) = \underset{\alpha, \beta: \alpha_i \geq 0}{\max} \mathcal{L}(x, \alpha, \beta)\]

Notiamo infatti che se un dato \(x\) viola i vincoli imposti da un qualche \(g_i(x)\) o \(h_i(x)\), allora il problema in alto non ha una soluzione finita. In particolare,

\[\theta_{\mathcal{P}}(x) = \begin{cases} f(x) \;\;&\;\; \text{ se } x \text{ soddisfa i vincoli primali} \\ \infty \;\;&\;\; \text{ altrimenti } \end{cases}\]

Da questo segue che il nostro problema primale può essere espresso nel seguente modo

\[\underset{x}{\min} \theta_{\mathcal{P}}(x) = \underset{x}{\min} \underset{\alpha, \beta: \alpha_i \geq 0}{\max} \mathcal{L}(x, \alpha, \beta)\]

Il valore ottimo di questo problema sarà denotato con \(p^*\).

Consideriamo adesso un problema leggermente diverso, che chiameremo problema "duale"

\[\theta_{\mathcal{D}}(\alpha, \beta) = \underset{x}{\min} \underset{\alpha, \beta: \alpha_i \geq 0}{\max} \mathcal{L}(x, \alpha, \beta)\]