SICP - Exercises - Chapter I

In here I have written my solution to the exercises found in the first chapter of sicp.

• Book: Structure and Interpretation of Computer Languages.

• Chapter: I, Building Abstraction with Procedures.

Here is a list of the exercies contained in this file:

Page 54.

Q: Find out the result in response to each following expression, assuming that the sequences are to be evaluated in the order in which it is presented.

A:

(define a 3)
(define b (+ a 1))
(if (and (> b a) (< b (* a b)))
    b
    a)

Result: 4

(define a 3)
(define b (+ a 1))
(cond ((= a 4) 6)
      ((= b 4) (+ 6 7 a))
      (else 25))

Result: 16

(define a 3)
(define b (+ a 1))
(+ 2 (if (> b a) b a))

Result: 6

(define a 3)
(define b (+ a 1))
(* (cond ((> a b) a)
         ((< a b) b)
         (else -1 ))
   (+ a 1))

Result: 16

Page 55.

Q: Translate the following expression into prefix form

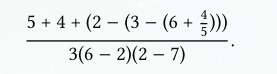
A:

(/ (+ 5
      4
      (- 2
         (- 3
            (+ 6
               (/ 4 5)))))
   (* 3
      (- 6 2)
      (- 2 7)))

Result: -37/150.

Page 55.

Define a procedure that takes three numbers as arguments and returns the sum of the squares of the two larger numbers.

(define (ex1.3 x y z)
  (cond ((and (> x y) (> y z)) (+ (* x x) (* y y))) ;; x > y > z
        ((and (> x z) (> z y)) (+ (* x x) (* z z))) ;; x > z > y

        ((and (> y x) (> x z)) (+ (* y y) (* x x))) ;; y > x > z
        ((and (> y z) (> z x)) (+ (* y y) (* z z))) ;; y > z > x

        ((and (> z y) (> y x)) (+ (* z z) (* y y))) ;; z > y > x
        ((and (> z x) (> x y)) (+ (* z z) (* x x))) ;; z > x > y
        ))

(ex1.3 2 5 10)

Result: 125

Page 55.

Q: Observe that our model of evaluation allows for combinations whose operators are compound expressions. Use this observation to describe the behavior of the following procedure:

(define (a-plus-abs-b a b)
  ((if (> b 0) + -) a b))

A: I'm tempted to believe that the if will return the + operator when b > 0 and the - operator when b <= 0 . If that is the case, then we'd have the following behavior

Let's test this out

(define (a-plus-abs-b a b)
  ((if (> b 0) + -) a b))

(a-plus-abs-b 10 10)
(a-plus-abs-b 10 -10)

Result: 20

It seems to work that way. I wonder if that's possible because the if itself is the in the operator place of the combination which defines the procedure.

Page 55

Ben Bitdiddle has invented a test to determine whether the interpreter he is faced with is using applicative-order evaluation or normal-order evaluation . He defines the following two procedures:

    (define (p) (p))
    (define (test x y)
      (if (= x 0) 0 y))

Then he evaluates the expression

  (test 0 (p))

Q1: What behavior will Ben observe with an interpreter that uses applicative-order evaluation ?

R1: With applicative order we first evaluate all operands to get the argumens right.

In our case this means that when we try to evaluate the expression (test 0 (p)), we have to evaluate the procedure p. Well, since the procedure p calls itself recursively without a base case, when we evaluate p we start an infinite loop that never ends.

Thus, with applicative-order evaluation the compiler will return nothing.

Q2: What behavior will Ben observe with an interpreter that uses normal-order evaluation ?

R2: With normal order we first expand the operator to obtain an expression, and we only evaluate operands when we reach a primitive procedure and their values are needed.

In our case this means that we immediatly evaluate the expression

(if (= 0 0) 0 (p))

since the predicate is true, we immediately return 0, and we never end up calling the p procedure.

Thus, with normal-order evaluation the compiler will return 0 .

Page 60.

Suppose we implement a new version of if using the cond construct

    (define (new-if predicate then-clause else-clause)
      (cond (predicate then-clause)
            (else else-clause)))

    (new-if (= 0 3) 0 5)

5

Q: Let us now use this version of if to rewrite the square-root program as follows.

    (define (sqrt-iter guess x)
      (new-if (good-enough? guess x)
              guess
              (sqrt-iter (improve guess x) x)))

Is there a problem with this?

A: The problem with this I think is the fact that Lisp implements an applicative order for standard procedures. Thus, before actually calling the new-if procedure, we have to evaluate all of its operands to get the relative arguments. To do this we have to call again sqrt-iter, so we would end up creating a never-ending loop.

We thus have to stick to using the provided special form that does not evaluates all of its operands.

Page 61.

Q1: Show that the definition of good-enough? provided in the textbook fails for small and large numbers.

A2: We get the following results

as we can see, from 0.0001 we already have a significant error.

Q1: Design a new square-root procedure where the end test measures how the guess value changes from one iteration to the next, and stops the computation once the change is very small.

A:

    (define (sqrt x)
      (sqrt-iter 1.0 1.1 x))

    (define (sqrt-iter old_guess guess x)
      (if (good-enough? old_guess guess)
          guess
          (sqrt-iter guess (improve guess x) x)))

    (define (improve guess x)
      (average guess (/ x guess)))

    (define (average x y)
      (/ (+ x y) 2))

    (define (good-enough? old_guess guess)
      (< (/ (abs (- guess old_guess))
            guess)
         0.001))

    (define (square x) (* x x))

    (define (abs x)
      (if (< x 0) (- x)
          x))

    (square (sqrt 0.0001)) 

1.0000000328143352e-4

This new implementation seems to work better for small numbers.

Page 74.

Q1: Using the substitution model illustrate the process generated by the following procedures and determine if they are recursive or iterative processes.

    (define (+ a b)
      (if (= a 0) b
          (inc (+ (dec a) b))))

    (+ 10 13)

A1: By showing the execution of (+ 4 5) we get the following

  (+ 4 5)
  (inc (+ 3 5))
  (inc (inc (+ 2 5)))
  (inc (inc (inc (+ 1 5))))
  (inc (inc (inc (inc (+ 0 5)))))
  (inc (inc (inc (inc 5))))
  (inc (inc (inc 6)))
  (inc (inc 7))
  (inc 8)
  9

Which is clearly a recursive process since we follow an expand-then-contract shape, and it stacks up a sequence of deferred operations (inc).

Q2: Do the same for the following procedure.

    (define (+ a b)
      (if (= a 0) b
          (+ (dec a) (inc b))))

A2: This time by showing the execution of (+ 4 5) we get the following

  (+ 4 5)
  (+ 3 6)
  (+ 2 7)
  (+ 1 8)
  (+ 0 9)

This time we get an iterative process, since at each step of the execution we only need to know the value of the two arguments a b to begin the execution once again, and at the end of the procedure the sum is stored in the second number, b.

Page 75.

The following procedure computes a mathematical function called Ackermann's function

    (define (A x y)
      (cond ((= y 0) 0)
            ((= x 0) (* 2 y))
            ((= y 1) 2)
            (else (A (- x 1) (A x (- y 1))))))

Q: Consider now the following procedues, and given for each coincise mathematical definitions for the functions computed by the procedures f, g and h for positive integer values of n.

    (define (f n) (A 0 n))
    (define (g n) (A 1 n))
    (define (h n) (A 2 n))
    (define (k n) (* 5 n n))

A:

• \(f(n) = 2 \cdot n\)

• \(g(n) = 2^n\)

• \(h(n)\) is a tower of \(n\) times \(2^2\).

Page 81.

Q1: A function \(f\) is defined by the following rule

\[f(n) = \begin{cases} n \,\,\,&,\,\,\, n < 3 \\ f(n-1) + 2f(n-2) + 3f(n-3) \,\,\,&,\,\,\, n \geq 3\\ \end{cases}\]

Write a procedure that computes \(f\) by means of a recursive process .

A1:

    (define (f-rec n) 
      (if (< n 3) n
          (+ (f-rec (- n 1))
             (* 2
                (f-rec (- n 2)))
             (* 3
                (f-rec (- n 3))))))

    (f-rec 10)

1892

Q2: Then write a procedure that computes \(f\) by means of an iterative process .

A2:

    (define (f n)
      (define (f-iter a b c count)
        (cond ((= n 0) 0)
              ((= n 1) 1)
              ((= n 2) 2)
              ((= count n) c)
              (else
               (f-iter  b 
                        c
                        (+ c (* 2 b) (* 3 a))
                        (+ count 1)))))
      (f-iter 0 1 2 2))
    (f 10)

1892

Page 81.

The Pascal's triangle has the following form

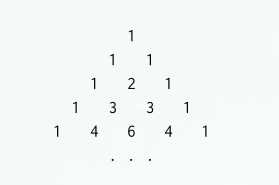
Q: Write a procedure that computes elements of Pascal's triangle by means of a recursive process.

R:

    (define (pascal-triangle row col)
      (define (pascal-triangle-rec row col)
        (cond  ((= row 1) 1)
               ((= col 1) 1)
               ((= col row) 1)
               (else 
                (+ 
                 (pascal-triangle-rec (- row 1) (- col 1))
                 (pascal-triangle-rec (- row 1) col)))))
      (if (> col row) -1
          (pascal-triangle-rec row col)))

[2020-09-16 mer 09:57]

Page 82.

Q: Prove that \(Fib(n)\) is the cloest integer to \(\frac{\phi^n}{\sqrt{5}}\), where

\[\phi = \frac{1 + \sqrt{5}}{2}\]

A: Let us first prove by induction that

\[Fib(n) := \frac{\phi^n - \psi^n}{\sqrt{5}}\]

where \(\psi^n := (1 - \sqrt{5})/2\).

• Base step: \((n=1)\):

  \[Fib(1) = \frac{\phi - \psi}{\sqrt{5}} = \frac{\Big(\frac{1 + \sqrt{5}}{2}\Big) - \Big(\frac{1 - \sqrt{5}}{2}\Big)}{\sqrt{5}} = \frac{\sqrt{5}}{\sqrt{5}} = 1\]

  \[\tag*{$\checkmark$}\]

• Inductive step: \((n > 1)\):

  The inductive step follows from the fact that both \(\phi\) and \(\psi\) have the following property

  \[\phi^2 = \Big( \frac{1 + \sqrt{5}}{2}\Big)^2 = \frac{1 + 2\sqrt{5} + 5}{4} = \frac{6 + 2\sqrt{5}}{4} = \frac{1 + \sqrt{5}}{2} + 1 = \phi + 1\]

  Indeed, by using this relation along side the inductive hypothesis (assumed for the case \(n-1\)), we get

  \[\begin{split} Fib(n) &= Fib(n-1) + Fib(n-2) \\ &= \frac{\phi^{n-1} - \psi^{n-1}}{\sqrt{5}} + \frac{\phi^{n-2} - \psi^{n-2}}{\sqrt{5}} \\ &= \frac{\phi^{n-2} \cdot (\phi + 1) - \psi^{n-2} \cdot (\psi + 1)}{\sqrt{5}} \\ &= \frac{\phi^{n-2} \cdot \phi^2 - \psi^{n-2} \cdot \psi^2}{\sqrt{5}} \\ &= \frac{\phi^n - \psi^n}{\sqrt{5}} \\ \end{split}\]

  \[\tag*{$\checkmark$}\]

We are now able to prove what was asked of us. Start by observing that

\[ -1 < \psi < 0 \implies -1 < \psi^n < 1\]

also, since \(\sqrt{5} > 2\), we have

\[ -\frac{1}{2} < - \frac{1}{\sqrt{5}} < \frac{\psi^n}{\sqrt{5}} < \frac{1}{\sqrt{5}} < \frac12\]

now we use the formula we have just proved to write

\[Fib(n) = \frac{\phi^n}{\sqrt{5}} - \frac{\psi^n}{\sqrt{5}} \iff \frac{\phi^n}{\sqrt{5}} = Fib(n) + \frac{\psi^n}{\sqrt{5}}\]

To finish off, consider

\[ -\frac12 < \frac{\psi^n}{\sqrt{5}} < \frac12\]

By adding \(Fib(n)\) to both sides we get

\[Fib(n) - \frac12 < Fib(n) + \frac{\psi^n}{\sqrt{5}} < Fib(n) + \frac12\]

which is equivalent of saying

\[Fib(n) - \frac12 < \frac{\phi^n}{\sqrt{5}} < Fib(n) + \frac12\]

This means that \(\phi^n/\sqrt{5}\) will never be further away from the value of \(Fib(n)\) than \(1\). Thus \(Fib(n)\) is the closest integer to \(\phi^n/\sqrt{5}\).

\[\tag*{$\blacksquare$}\]

[2020-09-16 mer 10:51]

Page 84.

Q1: Draw the tree illustrating the process generated by the count-change procedure in making change for 11 cents.

A1: The tree generated by the call (count-change 11) is the following

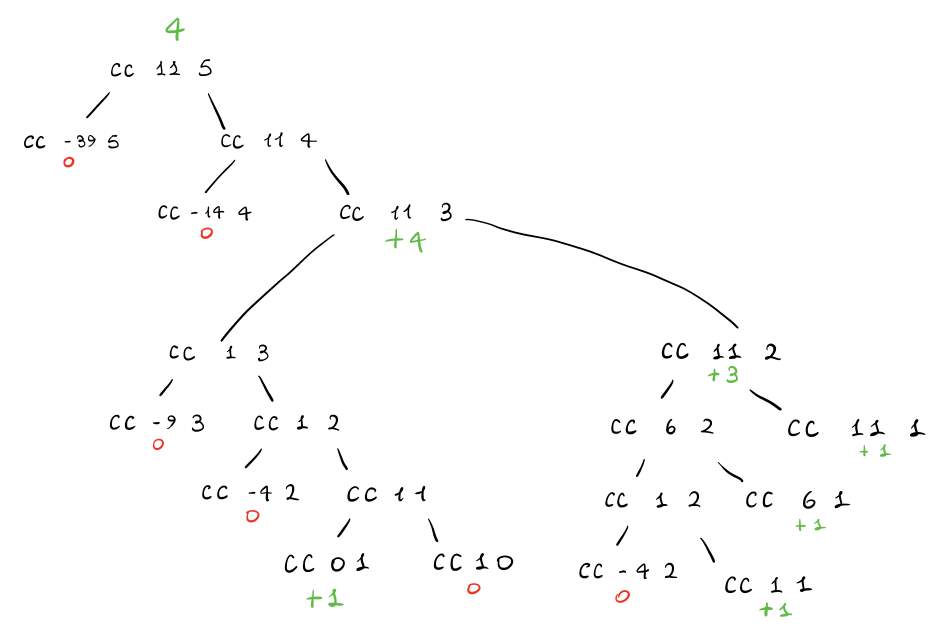
Q2: What are the order of growth of the space and number of steps used by this process as the mount to be changed increases?

A2: For the space complexity we have \(\theta(n)\), while for the time complexity we have \(\theta(n^5)\).

Page 84.

For small value of an angle \(x\) (specified in radians), we can compute the \(\sin{x}\) by using the approximation \(\sin{x} \approx x\). Also, to reduce the size of the argument of sin we can use the following trigonometric identity

\[\sin{x} = 3 \cdot \sin{\frac{x}{3}} - 4 \cdot \sin^3{\frac{x}{3}}\]

For this exercise we assume that "sufficiently small" is not grater than \(0.1\) radians.

We implement these ideas in the following procedures

    (define (cube x) (* x x x))
    (define (p x) 
    (- (* 3 x) (* 4 (cube x))))
    (define (sine angle)
      (if (not (> (abs angle) 0.1))
          angle
          (p (sine (/ angle 3.0)))))
    (sin 12.25)

Answer the following questions:

Q1: How many times is the procedure p applied when (sine 12.15) is evaluated?

A1: Since,

    12.15 / 3.0 => 4.05
    4.05  / 3.0 => 1.35
    1.35  / 3.0 => 0.45
    0.45  / 3.0 => 0.15
    0.15  / 3.0 => 0.05

we get that p is applied 5 times.

Q2: What is the order of growth in space and number of steps (as a function of a ) used by the process generated by the sine procedure when (sin a) is evaluated?

A2: Since we have \(\Theta(\log a)\) steps before we reach the base case, if we assume that multiplication is done in costant time then both space and time required is \(\Theta(\log a)\). Otherwise we get that the the space required is \(\Theta(\log a)\) while the time is \(O(a^3 \cdot \log a)\).

Page 88.

Q: Design a procedure that evolves an iterative exponentiation process that uses successive squaring and uses a logarithmic number of steps, as does in the following procedure, which instead produces a recursive process.

    (define (square n) (* n n))

    (define (even? n)
      (= (remainder n 2) 0))


    (define (fast-expt b n)
      (cond ((= n 0) 1)
            ((= n 1) b)
            ((even? n) (square (fast-expt b (/ n 2))))
            (else (* b (fast-expt b (- n 1))))))

    (fast-expt 2 10)

1204

A: The basic idea is to use the fact that

\[ (b^{\frac{n}{2}})^2 = (b^2)^{\frac{n}{2}}\]

and to keep, along with the exponent \(n\) and the base \(b\), an additional state variable \(a\). This state variable is used to define the state trasformation in such a way that the product \(a \cdot b^n\) is unchanged from state to state. At the the beginning of the process \(a\) is taken to be \(1\), and thus at the end of the process the answer is given by \(a\) itself.

After sometime I figured out how to do it: the idea is that the variable a is used to store the current value of b when n is odd and thus the following equation has to be used

\[b^n = b \cdot b^{n-1}\]

We thus define the following transformations, which depend on the particular value of \(n\):

• Case n even:

        a -> a 
        b -> b^2
        n -> n/2
  

• Case n odd:

        a -> a * b
        b -> b
        n -> n - 1
  

And we have that for each state transformation \(a \cdot b^n\) has the same value.

    (define (even? n) (= (remainder n 2) 0))
    (define (square n) (* n n))

    (define (expt b n)
      (define (expt-iter a b n)
        (cond ((= n 0) a)
              ((even? n) (expt-iter a (square b) (/ n 2)))
              (else (expt-iter (* a b) b (- n 1)))))
      (expt-iter 1 b n))

    (expt 10 3)

1000

Page 88.

In a similar vein as what was shown for the exponentiation by means of repeated multiplication, one can perform integer multiplication by means of repeated addition.

The following procedure is analogous to the expt produce, but it is for multiplication. Notice that the process takes a number of steps that is linear in b .

    (define (* a b)
      (if (= b 0)
          0
          (+ a (* a (- b 1)))))

Suppose now we have a double operation, which doubles an integer, and a halve operation, which divies an (even) integer by 2 .

Q: Using these, design a multiplication produce analogous to fast-expt that uses a logarithmic number of steps.

A:

    (define (even? n) (= (remainder n 2) 0))
    (define (double n) (+ n n))
    (define (halve n) (/ n 2))

    (define (fast-mult a b)
      (cond ((= b 0) 0)
            ((= b 1) a)
            ((even? b) (fast-mult (double a) (halve b)))
            (else (+ a (fast-mult a (- b 1))))))

    (fast-mult 10 30)

300

Page 89.

Q: Using the results of exercises 1.16 and 1.17 devise a procedure that generates an iterative process for multiplying two integers in terms of adding, double, and halving and uses a logarithmic number of steps.

A: In this case the state transformations are defined as follows, depending on the value of b:

• Case b odd:

        a -> a
        b -> b - 1
        c -> c + 1
  

• Case b even:

        a -> 2a
        b -> b/2
        c -> c
  

    (define (double n) (+ n n))
    (define (halve n) (/ n 2))
    (define (even? n) (= (remainder n 2) 0))

    (define (mult a b)
      (define (mult-iter a b c)
        (cond ((= b 0) c)
              ((even? b) (mult-iter (double a) (halve b) c))
              (else (mult-iter a (- b 1) (+ c a)))))
      (mult-iter a b 0))

    (mult 25 30)

750

Page 89.

There is a clever and efficient algorithm for computing the FIbonacci numbers in a logarithmic number of steps.

After some computation was done the result obtain was the following

• p' = q^2 + p^2

• q' = 2pq + q^2

we thus obtain the following procedure, which computes Fibonacci number in a logarithmic number of steps.

    (define (fib n)
      (fib-iter 1 0 0 1 n))

    (define (fib-iter a b p q count )
      (cond ((= count 0) b)
            ((even? count)
             (fib-iter a
                       b
                       (+ (* q q) (* p p))
                       (+ (* 2 p q) (* q q))
                       (/ count 2)))
            (else (fib-iter (+ (* b q) (* a q) (* a p))
                            (+ (* b p) (* a q))
                            p 
                            q
                            (- count 1)))))

    (fib 30)

832040

Page 93.

Q: Using the substitution method (for normal order), illustrate the process generated in evaluating (gcd 206 40) and count the remainder operations that are actually performed.

    (define (gcd a b)
      (if (= b 0) a
          (gcd b (remainder a b))))

    (gcd 206 40)

A: Normal-order evaluation executes the remainder operation many times, because it keeps all the remainder operation in a stack when calling recursively the function, and at each call it executes the entire local stack when it has to compare the value of b with 0. In particular we get the following

• We begin by the call (gcd 206 40) , which calls the new function (gcd 40 (remainder 206 40)) . Notice that the operands are not evaluated, because we are executing under normal order.

• The call (gcd 40 (remainder 206 40)) has to evaluate (remainder 206 40) because it needs to check if b is equal to 0 . By evaluating it we get 6 , and since 6 is not equal to 0 it calls (gcd 6 (remainder 40 (remainder 206 40))) .

• The call (gcd 6 (remainder 40 (remainder 206 40))) evaluates (remainder 40 (remainder 206 40)) to get 4 and since 4 is not equal to 0 it calls (gcd 4 (remainder 6 ~(gcd 6 (remainder 40 (remainder 206 40))))) .

• ...

In total we have 18 calls to remainder.

Applicative-order evaluation instead executes the remainder operation 4 times.

Page 98

Q: Use the smallest-divisor procedure, which is repoted below to find the smallest divisor for each of the following number: 199, 1999, 19999.

    (define (square a) (* a a))
    (define (divides? a b) (= (remainder b a) 0))

    (define (smallest-divisor n) (find-divisor n 2))
    (define (find-divisor n test-divisor)
      (cond ((> (square test-divisor) n) n)
            ((divides? test-divisor n) test-divisor)
            (else (find-divisor n (+ test-divisor 1)))))

A:

[2020-09-17 gio 00:02]

Page 98.

This exercise could not be done properly as I have not yet found a good alternative to the runtime discused in here.

Page 100.

Q: Change the procedure smallest-divisor so that the values used for test-divisor are not 2, 3, 4, 5, 6 but rather 2, 3, 5, 7, 9 , that is, after checking that the number is divisible by 2 there is no point in checking to see if it is divisible by any larger even numbers. To do so define a procedure next that returns 3 if its input is equal to 2 and otherwise returns its intput plus 2 . Modify the smallest-divisor procedure to use this procedure.

A:

   (define (square a) (* a a))

   (define (divides? a b) (= (remainder b a) 0))

   (define (next a)
     (if (= a 2)
         3
         (+ a 2)))

   (define (find-divisor n test-divisor)
     (cond ((> (square test-divisor) n) n)
           ((divides? test-divisor n) test-divisor)
           (else (find-divisor n (next test-divisor)))))

   (define (smallest-divisor n) (find-divisor n 2))

   (define (prime? n)
     (= n (smallest-divisor n)))

   (prime? 15)

[2020-09-17 gio 01:07]

Page 100.

Can't really be done because runtime is missing in the scheme version I am really using.

[2020-09-17 gio 00:11]

Page 100.

Q: Is it true that instead of writing our expmod procedure we could have used our fast-exp procedure as follows

    (define (expmod base exp m)
      (remainder (fast-expt base exp) m))

Would this procedure serve as well for our fast prime test?

A: No, it would not, because we are not reducing mod m everytime we do the exponentiation, and so the total complexity is more like base^exp rather than m^3 . This means that the intermediate results obtained by this modified version of expmod are huge.

[2020-09-17 gio 00:18]

Page 101.

Q: Why the following code now costs \theta(n) instead of \theta(\log n) ?

    (define (expmod base exp m)
      (cond ((= exp 0) 1)
            ((even? exp)
             (remainder (* (expmod base (/ exp 2) m)
                           (expmod base (/ exp 2) m))
                        m))
            (else
             (remainder (* base
                           (expmod base (- exp 1) m)) 
                        m))))

A: Because when the argument is even we make two recursive call of the form (expmod base (/ exp 2) m) which create the following recursion

\[T(n) = 2 \cdot T(n/2) + \theta(1)\]

which has for solutions

\[T(n) = O(n\log n)\]

Page 101.

Q: Demonstrate that the Carmichael numbers really do fool the Fermat test. To do so write a procedure that takes an integer \(n\) and tests wheter \(a^n\) is congruent to \(a\) modulo \(n\) for every \(a < n\), and try the procedure for the given Carmichael numbers.

561, 1105, 1729, 2465, 2821, 6601

A:

    (define (even? n) (= (remainder n 2) 0))
    (define (square n) (* n n))

    ;; computes exponential mod in logarithmic time
    (define (expmod base exp m)
      (cond ((= exp 0) 1)
            ((= exp 1) base)
            ((even? exp)
             (remainder
              (square (expmod base (/ exp 2) m))
              m))
            (else
             (remainder
              (* base (expmod base (- exp 1) m))
              m))))

    (define (carmichael? n)
      (define (carmichael-iter a n)
        (cond ((= a n) #t)
              ((not (= (expmod a n n) a)) #f)
              (else (carmichael-iter (+ a 1) n))))
      (carmichael-iter 2 n))

    (carmichael? 6601)

#t

Page 101.

The Miller-Rabin test is another primality test that is more robust than the Fermat test, because it cannot be fooled by Carmichael numbers.

To test the primality of a number \(n\) by using the Miller-Rabin test we pick a random number \(a < n\) and raise \(a\) to the \((n-1)\) power modulo \(n\) using the usual expmod procedure. When we perform the squaring step however we check to see if we have discovered a non trivial square root of 1 modulo n , that is, a number not equal to 1 or n-1 whose square is equal to 1. It is possible to prove that the existence of such trivial roots implies that the number is not prime.

Q: Implement this test by modifying the expmod procedure to signal if it discovers a nontrivial square root of 1.

   (define (even? n) (= (remainder n 2) 0))
   (define (square n) (* n n))

   (define (decompose n)
     (define (decompose-iter n count)
       (if (and (not (= n 0))
                (= (remainder n 2) 0))
           (decompose-iter (/ n 2) (+ count 1))
           (list n count)))
     (decompose-iter n 0))

   ;; computes exponential mod in logarithmic time
   (define (expmod base exp m)
     (cond ((= exp 0) 1)
           ((= exp 1) base)
           ((even? exp) (remainder
                         (square (expmod base (/ exp 2) m))
                         m))
           (else (remainder
                  (* base (expmod base (- exp 1) m))
                  m))))

   (define (witness a n)
     (define (witness-iter count base)
       (cond ((and (= count 0)
                   (not (= base 1))) #t)
             ((and (= count 0)
                   (= base 1)) #f)
             ((and (not (= base 1))
                   (not (or (= base -1) (= base (- n 1))))
                   (= (expmod base 2 n) 1)) #t)
             (else (witness-iter (- count 1) (expmod base 2 n)))))
     (witness-iter (cadr (decompose (- n 1)))
                   (expmod a (car (decompose (- n 1))) n)))

   (define (miller-rabin n)
     (witness (+ 1 (random (- n 1))) n))

#f

Page 108.

Simpon's Rule is a more method of numerical integration. Using Simpon's Rule, the integral of a function \(f\) between \(a\) and \(b\) is approximated as

\[\frac{h}{3} \cdot \Big(y_0 + 4y_1 + 2_y2 + 4_y3 + 2_y4 + ... + 2y_{n-2} + 4y_{n-1} + y_n\Big)\]

where \(h = (b - a)/n\) for some even integer \(n\) and \(y_k = f(a + k \cdot h)\).

Q: Define a procedure that takes as arguments \(f, a, b\) and \(n\) and returns the value of the integral, computed using Simpson's Rule.

A:

    (define (cube n) (* n n n))

    (define (even? n) (= (remainder n 2) 0))

    (define (simpson-rule f a b n)
      (define (simpson-term k h) (f (+ a (* k h))))
      (define (simpson-rule-sum total count h)
        (cond ((= count 0) (simpson-rule-sum (f a) (+ count 1) h))
              ((= count n) (* (/ h 3)
                              (+ total (simpson-term n h))))

              ((even? count) (simpson-rule-sum (+ total (* 2 (simpson-term count h)))
                                               (+ count 1)
                                               h))
              (else (simpson-rule-sum (+ total (* 4 (simpson-term count h)))
                                      (+ count 1)
                                      h))))
      (simpson-rule-sum 0 0 (/ (- b a) n)))

    (simpson-rule cube 0 1 10000.0)

0.2500000000000001

Page 108.

Q: The general sum procedure we saw generates a linear recursion.

    ;; generates recursive process
    (define (rec-sum term a next b)
      (if (> a b)
          0
          (+ (term a)
             (rec-sum term (next a) next b))))

Rewrite the procedure so that it is performeted iteratively.

A:

    ;; generates iterative process
    (define (iter-sum term a next b)
      (define (iter a result)
        (if (> a b) 
            result
            (iter (next a) (+ (term a) result))))
      (iter a 0))

    ;; test it out
    (define (inc n) (+ n 1)) 
    (define (cube n) (* n n n))

    (define (sum-cubes a b)
      (iter-sum cube a inc b))

    (sum-cubes 1 10)

3025

Page 109.

Q1: Write a general procedure called product that returns the product of the values of a function at points over a given range.

A1:

    ;; computes f(a_1) * f(a_2) * ... * f(a_n)
    (define (rec-prod term a next b)
      (if (> a b)
          1
          (* (term a)
             (rec-prod term (next a) next b))))

Q2: Show how to define factorial in terms of product .

A2:

    (define (identity x) x)
    (define (next x) (+ x 1))

    (define (factorial n)
      (rec-prod identity 1 next n))

    (factorial 10)

3628800

Q3: Use product to compute an approximation of pi using following following formula

\[\frac{\pi}{4} = \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} ...\]

A3:

    (define (even? n) (= (remainder n 2) 0))
    (define (square n) (* n n))

    (define (rec-prod term a next b)
      (if (> a b)
          1
          (* (term a)
             (rec-prod term (next a) next b))))

    (define (identity x) x)
    (define (next x) (+ x 2))

    ;; assumes max >= 4
    (define (pi-approx max)
      (cond ((even? max) (/ (* 2.0 (square (rec-prod identity 4 next max)))
                            (* (+ max 1) (square (rec-prod identity 3 next (- max 1))))))
            (else (pi-approx (- max 1)))))

    (* (pi-approx 100) 4)

3.1260789002154112

Q4: Write the iterative version of the general product procedure.

A4:

    (define (prod-iter term a next b)
      (define (iter a result)
        (if (> a b)
            result
            (iter (next a) (* result (term a)))))
      (iter a 1))

Page 110.

Q1: Show that sum and product are both special cases of a more general notion called accumulate that combines a collection of terms using some general accumulation function

(accumulate combiner null-value term a next b)

The combiner procedure takes two arguments and specifies how the current term is to be combined with the accumulation of the preceding terms, while the null-value is the value to be used when terms run out.

Write the accumulate procedure and show how sum and product can both be defined as simple calls to accumulate

A1:

    (define (accumulate-rec combiner nill-value term a next b)
      (if (> a b)
          nill-value
          (combiner (term a)
                    (accumulate-rec combiner nill-value term (next a) next b))))


    (define (sum term a next b)
      (accumulate-rec + 0 term a next b))

    (define (product term a next b)
      (accumulate-rec * 1 term a next b))


    (define (identity x) x)
    (define (succ x) (+ x 1))
    (sum identity 1 succ 3)
    (product identity 1 succ 3)

Q2: Write the iterative version of the accumulate procedure.

A2:

    (define (accumulate-iter combiner nill-value term a next b)
      (define (iter a result)
        (if (> a b)
            result
            (iter (next a) (combiner result (term a)))))
      (iter a nill-value))

    (define (identity x) x)
    (define (succ x) (+ x 1))
    (define (product term a next b)
      (accumulate-iter * 1 term a next b))

    (product identity 1 succ 5)

120

Page 110.

Q1: There is an even more general version of accumulate , which is obtained by introducing the notion of a filter on the terms to be combined. The idea is to combine only those terms derived from values in the range that satisfy a specified condition.

Write the filtered-accumulate prodedure.

A1:

    (define (filtered-accumulate combiner filter null-value term a next b)
      (define (iter a result)
        (cond ((> a b) result)
              ((filter a) (iter (next a) (combiner a result)))
              (else (iter (next a) result))))
      (iter a null-value))

Q2: Show how to express the following using filtered-accumulate

• The sum of the squares of the prime numbers in the interval a to b assuming you have a prime? predicate.

        (define (square a) (* a a))
        (define (divides? a b) (= (remainder b a) 0))
  
        (define (smallest-divisor n) (find-divisor n 2))
        (define (find-divisor n test-divisor)
          (cond ((> (square test-divisor) n) n)
                ((divides? test-divisor n) test-divisor)
                (else (find-divisor n (+ test-divisor 1)))))
  
        (define (prime? n)
          (= n (smallest-divisor n)))
  
        ;; --------------------------
  
        (define (id x) x)
        (define (succ x) (+ x 1))
  
        (define (filtered-accumulate combiner filter null-value term a next b)
          (define (iter a result)
            (cond ((> a b) result)
                  ((filter a) (iter (next a) (combiner (term a) result)))
                  (else (iter (next a) result))))
          (iter a null-value))
  
        (define (sum-squares-of-primes a b)
          (filtered-accumulate + prime? 0 square a succ b))
  

• The product of all the positive integers less than n that are relatively prime to n .

        (define (gcd a b)
          (if (= b 0) a
              (gcd b (remainder a b))))
  
        (define (coprime? a b)
          (= (gcd a b) 1))
  
        ;; ;; -------------------------
  
        (define (id x) x)
        (define (succ x) (+ x 1))
  
        (define (filtered-accumulate combiner filter null-value term a next b)
          (define (iter a result)
            (cond ((> a b) result)
                  ((filter a) (iter (next a) (combiner a result)))
                  (else (iter (next a) result))))
          (iter a null-value))
  
        (define (product-of-coprimes n)
          (filtered-accumulate * (lambda (x) (coprime? n x)) 1 id 1 succ n))
  
        (product-of-coprimes 9)
  

Page 116.

Q: Consider the following code. What happens if we ask the interpreter to evaluate the combination (f f) ?

  (define (square n) (* n n))
  (define (f g) (g 2))
  (f square) ;; 4
  (f (lambda (z) (* z (+ z 1)))) ;; 6

A: The interpreter would incurr in an error while trying to evaluate the combination (2 2) .

  (f f)
  (f 2)
  (2 2)

[2020-09-16 mer 18:13]

Page 122.

Q1: Show that the golden ratio is a fixed point of the transformation

\[x \to 1 + \frac{1}{x}\]

A2: Se definimo \(g(x) := 1 + 1/x\), notiamo che

\[\begin{split} g(\phi) = 1 + \frac{1}{\phi} = 1 + \frac{1}{\frac{1 + \sqrt{5}}{2}} &= 1 + \frac{2}{1 + \sqrt{5}} \\ &= \frac{3 + \sqrt{5}}{1 + \sqrt{5}} \\ &= \frac{3 + \sqrt{5}}{1 + \sqrt{5}} \cdot \frac{1}{1}\\ &= \frac{3 + \sqrt{5}}{1 + \sqrt{5}} \cdot \frac{1 - \sqrt{5}}{1 - \sqrt{5}}\\ &= \frac{3 - 3 \sqrt{5} + \sqrt{5} - 5}{1 - 5} \\ &= \frac{-2 -2\sqrt{5}}{-4} \\ &= \frac{1 + \sqrt{5}}{2} \\ &= \phi \end{split}\]

dunque \(g(\phi) = \phi\).

\[\tag*{$\blacksquare$}\]

Q2: Use this fact to computed it using the fixed-point procedure.

A2:

    (define (abs x)
      (if (< x 0) (- x)
          x))

    (define tolerance 0.00001)

    (define (fixed-point f first-guess)
      (define (close-enough? v1 v2) (< (abs (- v1 v2)) tolerance))
      (define (try guess)
        (let ((next (f guess)))
          (if (close-enough? guess next)
              next
              (try next))))
      (try first-guess))

      (fixed-point (lambda (x) (+ 1 (/ 1 x))) 1.0)

1.6180327868852458

Page 122.

Q1: Modify fixed-point so that it prints the sequence of approximations it generates, using newline and display primitives.

A1:

    (define (abs x)
      (if (< x 0) (- x)
          x))

    (define tolerance 0.00001)

    (define (fixed-point f first-guess)
      (define (close-enough? v1 v2) (< (abs (- v1 v2)) tolerance))
      (define (try guess)
        (let ((next (f guess)))
          (cond ((close-enough? guess next) next)
                (else
                 (newline)
                 (display next)
                 (try next)))))
      (try first-guess))

      (fixed-point (lambda (x) (+ 1 (/ 1 x))) 1.0)

Q2: Find a solution to \(x^x = 1000\) by finding a fixed point of

\[x \to \frac{\log(1000)}{\log(x)}\]

A2:

  (fixed point (lambda (x) (/ (log 1000) (log x))) 1.05)

4.555529419487897

Q3: Compare the number of steps this takes with and without average dumping.

A3:

    ;; steps taken without average dumping = 36
    (fixed point (lambda (x) (/ (log 1000) (log x))) 1.05)

    ;; steps taken with average dumping = 13
    (fixed point (lambda (x) (/ x (/ (log 1000) (log x)))) 1.05)

[2020-09-16 mer 18:44]

Page 123.

Q1: Define a prodecure cont-frac such that evaluating (cont-frac n d k) computes the value of the k-th term finite continued fraction, where n and d are one-argument procedures used to evaluate the terms N_i and D_i .

A1:

    (define (cont-frac n d k)
      (define (cont-frac-rec i)
        (if (= i k)
            0
            (/ (n i)
               (+ (d i)
                  (cont-frac-rec (+ i 1))))))
      (cont-frac-rec 1))

Q2: Check your procedure by approximating \(1/\phi\) using the following for successive value of \(k\). How large must you make \(k\) in order to get an approximation that is accurate to \(4\) decimal places?

A2:

    (define (cont-frac n d k)
      (define (cont-frac-rec i)
        (if (= i k)
            0
            (/ (n i)
               (+ (d i)
                  (cont-frac-rec (+ i 1))))))
      (cont-frac-rec 1))

    (cont-frac (lambda (i) 1.0) (lambda (i) 1.0) 12)

0.6180555555555556

With \(k=12\) we get \(4\) decimal places.

Q3: Write a cont-frec procedure that generates an iterative process.

A3:

    (define (cont-frac n d k)
      (define (cont-frac-iter result i)
        (if (= i 0) result
            (cont-frac-iter (/ (n i) (+ (d i) result)) (- i 1))))
      (cont-frac-iter (/ (n k) (d k)) (- k 1)))
    (cont-frac (lambda (i) 1.0) (lambda (i) 1.0) 12)

0.6180257510729613

Page 124.

Q: In 1737 Euler proved a way to approximate \(e-2\) with the following continued fraction expansion.

Write a program that uses your cont-frac procedure to approximate \(e\) based on Euler's expansion.

A:

    (define (cont-frac n d k)
      (define (cont-frac-iter result i)
        (if (= i 0) result
            (cont-frac-iter (/ (n i) (+ (d i) result)) (- i 1))))
      (cont-frac-iter (/ (n k) (d k)) (- k 1)))

    (define (d i)
      (cond ((or (= i 1)
                 (= (remainder (- i 1) 3) 2)
                 (= (remainder (- i 1) 3) 0)) 1)
            ((= i 2) 2)
            (else
             (+ 2 (* 2 (floor (/ (- i 1) 3)))))))

    (+ (cont-frac (lambda (i) 1.0) d 12) 2)

2.7182818229439496

Page 124.

Q: Define a prodedure called (tan-cf x k) that computes an approximation to the tangent function based on Lambert's formula , which is the following,

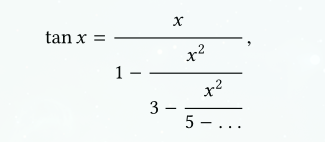
where k specifies the number of terms to compute.

A:

    (define (cont-frac n d k)
      (define (cont-frac-iter result i)
        (if (= i 0) result
            (cont-frac-iter (/ (n i) (+ (d i) result)) (- i 1))))
      (cont-frac-iter (/ (n k) (d k)) (- k 1)))

    (define (tan-cf x k)
      (define (d i) (- (* 2 i) 1))
      (define (n i)
        (if (= i 1) x
            (- (* x x))))
      (cont-frac n d k))

    (tan-cf 1.05 10)

Page 131

Q: Define a procedure cubic that can be used together with the newtons-method procedure in expressions of the form

(netwons-method (cubic a b c) 1)

to approximate zeros of the cubic \(x^3 + ax^2 + bx + c\). To do so remember that netwons method was implemented in the following way

• Fixed-point implementation

        (define (abs x)
          (if (< x 0) (- x)
              x))
  
        (define tolerance 0.00001)
  
        (define (fixed-point f first-guess)
          (define (close-enough? v1 v2) (< (abs (- v1 v2)) tolerance))
          (define (try guess)
            (let ((next (f guess)))
              (cond ((close-enough? guess next) next)
                    (else
                     (try next)))))
          (try first-guess))
  

• Neton's Method

        ;; To compute derivatives
        (define dx 0.00001)
        (define (deriv g)
          (lambda (x) (/ (- (g (+ x dx)) (g x)) dx)))
  
        ;; To implement netwon's method
        (define (netwon-transform g)
          (lambda (x) (- x (/ (g x) ((deriv g) x)))))
  
        (define (newtons-method g guess)
          (fixed-point (netwon-transform g) guess))
  

A:

    (define (square x) (* x x))
    (define (cube x) (* x x x))

    (define (cubic a b c) 
      (lambda (x) (+ 
                   (cube x)
                   (* a (square x))
                   (* b x)
                   c)))

    (newtons-method (cubic -2 3 2) 1.0)

-0.477967243009007

Page 131.

Q1: Define a procedure double that takes a procedure of one argument as argument and returns a procedure that applies the original procedure twice.

A1:

    (define (inc n) (+ n 1))
      (define (double f)
        (lambda (x) (f ( f x))))

    (((double (double double)) inc) 5)

Q2: What value is returned by the expression (((double (double double)) inc) 5) ?

A2: 21.

Indeed, when we call (double double) we are creating a procedure that applies two times the procedure double , which in itself applies two times the function given as argument. Thus (double double) applies 4 times the procedure given as argument. By following the same logic we have that (double (double double)) returns a procedure which, given a procedure f as argument, applies 4^2 = 16 times the procedure f .

Page 131.

Given two one-argument functions \(f\) and \(g\), their composition is defined as the function

\[x \to f(g(x))\]

Q: Define a procedure compose that implements the composition of functions.

A:

    (define (square x) (* x x))
    (define (inc n) (+ n 1))

    (define (compose f g)
      (lambda (x) (f (g x))))

    ((compose square inc) 6)

Page 132

If f is a numerical function and n is a positive integer, we can form the n-th repeated application of f , which is defined to be the function whose value at x is f(f(...(f(x))...)) .

Q: Write a procedure that takes as inputs a procedure that computes f and a positive integer n and returns the procedure that computes the n-th repeated application of f .

A:

    (define (square x) (* x x))

    (define (compose f g)
      (lambda (x) (f (g x))))

    (define (repeated f n)
      (define (repeated-iter comp count)
        (if (= count n)
            comp
            (repeated-iter (compose f comp) (+ count 1))))
      (repeated-iter f 1))

    ((repeated square 2) 5)

625

Page 132.

If f is a function and dx is some small number, then the smoothed version of f is the function whose value at a point x is the average of f(x - dx) , f(x) and f(x + dx) .

Q1: Write a procedure smooth that takes as input a procedure that computes f and returns a procedure that computes the smoothed f .

A1:

    (define dx 0.0001)
    (define (smooth f)
      (lambda (x) (/
                   (f (- x dx))
                   (f x)
                   (f (+ x dx)))))

Q2 Show how to generate the n-fold smoothed function by using the procedure repeated from exercise 1.43.

A2:

  (repeated smooth n)

Average 133

Q1: Do some experiments to determine how many average dumps are required to compute n-th roots as a fixed-point search based upon repeated average damping of y -> x/y^{n-1} .

    (define (square x) (* x x))

    (define (cube x) (* x x x))

    (define (expt b n)
      (define (expt-iter a b n)
        (cond ((= n 0) a)
              ((even? n) (expt-iter a (square b) (/ n 2)))
              (else (expt-iter (* a b) b (- n 1)))))
      (expt-iter 1 b n)) 

    ;; ------------------------------------
    (define (abs x)
      (if (< x 0) (- x)
          x))

    (define tolerance 0.00001)

    (define (fixed-point f first-guess)
      (define (close-enough? v1 v2) (< (abs (- v1 v2)) tolerance))
      (define (try guess)
        (let ((next (f guess)))
          (cond ((close-enough? guess next) next)
                (else
                 (try next)))))
      (try first-guess))

    ;; ------------------------------------
    (define (average a b) (/ (+ a b) 2))

    (define (average-damp f)
      (lambda (x) (average x (f x))))

    ;; ------------------------------------
    (define (compose f g)
      (lambda (x) (f (g x))))

    (define (repeated f n)
      (define (repeated-iter comp count)
        (if (= count n)
            comp
            (repeated-iter (compose f comp) (+ count 1))))
      (repeated-iter f 1))

A1: After some messing around I think that when computing the n-th root, the number of times we must average-damp is equal to the cloest power of 2 to our number. The following table will help

Thus we should simply get the floor of log_2(n).

Q2: Use this to implement a simple procedure for computing n-th root using fixed-point , average-dump and the repeated procedure.

A2:

    (define (base-log b x)
      (/ (log x) (log b)))

    (define (nth-root n x)
      (fixed-point
       ((repeated average-damp
                  (floor (base-log 2 n))) (lambda (y) (/ x (expt y (- n 1)))))
       1.0))

    (display (nth-root 42 12))

1.0609514824509467

Page 133.

Iterative improvement is a general computational strategy which says that, to compute something, start with an initial guess for the answer, test if the guess is good enough, and otherwise improve the guess and continue the process using the improved guess as the new guess.

Q1: Write a procedure iterative-improve that takes the following two procedures as arguments

1. A method for telling whether a guess is good enough

2. A method for improving a guess

and returns as its value a procedure that takes a guess as argument and keeps improving the guess until it is good enough.

A1:

    (define (average x y)
      (/ (+ x y) 2))

    (define (square x) (* x x))

    (define (abs x)
      (if (< x 0) (- x)
          x))

    (define (close-enough? x y)
      (< (abs (- y x) 0.001)))

    ;; ---------------------------

    (define (iterative-improve improve good-enough?)
      (lambda (guess)
        (if (good-enough? guess)
            guess
            ((iterative-improve improve good-enough?) (improve guess)))))

Q2: Rewrite the sqrt procedure and the fix-point procedure in terms of terms of iterative-improve .

    (define (sqrt x)
      ((iterative-improve
        (lambda (y) (average y (/ x y)))
        (lambda (y) (< (abs (- (square y) x)) 0.001)))
       1.0))

    (sqrt 2)

1.4142156862745097

    (define (my-fixed-point f first-guess)
      ((iterative-improve
        f
        (lambda (y) (< (abs (- y (f y))) 0.000001)))
       first-guess))

    (my-fixed-point cos 1.0)

0.7390845495752126