SICP 01A - Introduction to LISP

An example of declarative knowledge, of "what is true", is the definition of a square root.

Def: the square root \(\sqrt{x}\) of a number \(x\) is the number \(y\) such that

\[y^2 = x, \,\,\, y \geq 0\]

Notice that this definition tells us nothing on how to compute square roots. That is, if I give you a number, say \(5\), and I asked you to compute \(\sqrt{5}\), the only thing you know is that you need to find an \(y \geq 0\) such that \(y^2 = 5\), but you have no idea on where to find such a number.

To compute square roots we need another kind of knowledge, procedural knowledge, which deals with the "how to" do stuff. In this case in particular we want a procedure that, given a number \(x\), it lets us find an approximation of \(\sqrt{x}\).

Such a procedure is the following algorithm, due to Hero of Alexandria, and it works as follows:

• make an initial guess \(g\).

• improve guess by averaging \(g\) and \(x/g\).

• Keep improving the guess until it is "good enough".

Later on in the lecture we will implement such algorithm in LISP.

A process is like a magical spirit that lives in the computer and does something.

What directs a process is a pattern of rules called a procedure. Procedures are the spells that control this magical spirits that are the processes.

Procedures are written out with symbols using so-called programming languages. An example of a programming language is the LISP language. LISP can be sort-of compared to chess: its basic components are easily understood, just like chess rules are easy to explain, and these basic components allow one to build extremely complex system that are hard to understand.

In Computer science we are in the business on formalizing "how-to" imperative knowledge, and the real problems come out when we try to build very large systems.

The only reasons why building such complex systems is possible is because there are techniques for controlling the complexity of these large systems. This course is about such techniques.

There is a difference between the complexity a typical engineer faces for example when designing an airline and the complexity that a computer scientist faces. The difference is that, sometimes, Computer Science is simply not real, because in computer science we work with so-called idealized components, meaning that we can know as much as we want about programs and data piece that we're fitting together. We don't have to worry about tollerance. The consequence of this is that when building a complex system, there is not much difference between what I can build and what I can imagine.

While other engineers have to deal with physical constraints, the constrainted imposed by building large software systems are the limitations of our minds. In this sense computer science is not real: it is an abstract form of engineering, since we ignore the constraints that are imposed by reality.

The idea behind black-box abstraction is to take something and to build a box around it. For example we can build a box around the square root and only see how the inputs are mapped to outputs, and not the internals of what is going on.

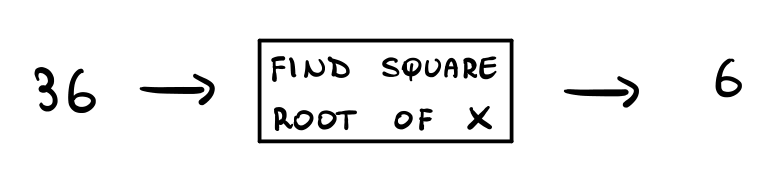
We use this kind of technique for:

1. Suppress detail for building bigger boxes.

2. Your how-to method may be an instance of a more general thing, and you want your language to express such generality.

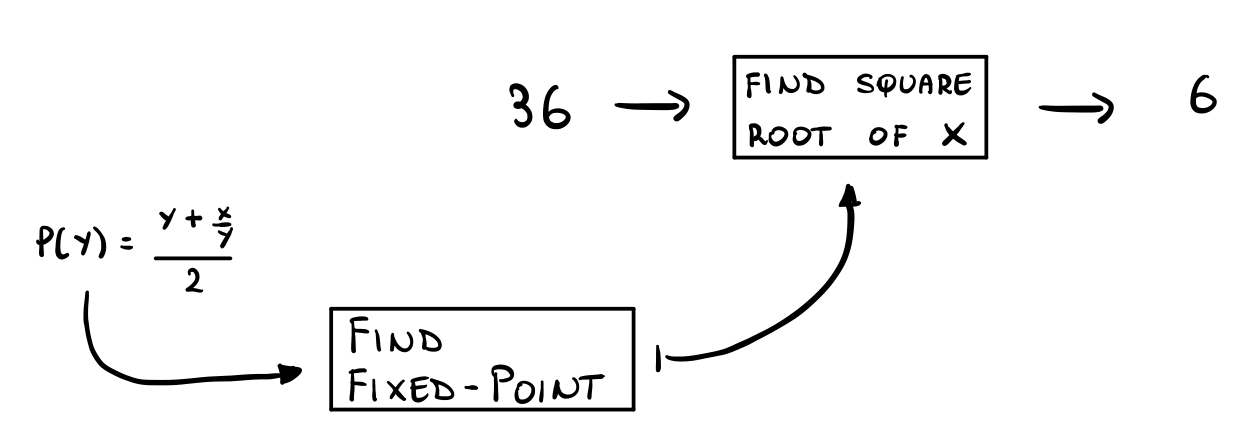
For example, the square root approximation method we have described before is a specialization of a more general method called a fixed-point scheme, which, given a function \(F(\cdot)\), it tries to find a value \(y\) for which

\[y = F(y)\]

The scheme is described as follows

• Start with a guess for \(y\).

• Keep applying \(F(\cdot)\) over and over until the result doesn't change very much.

Notice that if we are able to solve this more general problem then we can also approximate square root. Indeed, consider the following function

\[f(y) = \frac{y + \frac{x}{y}}{2}\]

then we have that if \(y\) is a fixed point of such function then

\[\begin{split} y = f(y) &\iff y = \frac{y + \frac{x}{y}}{2} \\ &\iff 2y = y + \frac{x}{y} \\ &\iff y = \frac{x}{y} \\ &\iff y^2 = x \\ &\iff y = \sqrt{x} \\ \end{split}\]

\[\tag*{$\checkmark$}\]

With this black-box abstraction technique we can thus have boxes that take in input other boxes and give in output even other boxes.

In terms of LISP functionalities that allow the usage of this black-box technique, we will see the following ones:

• Primtive Objects:

  • Primitive procedures

  • Primitive data

• Means of combination:

  • Procedure composition

  • Construction of compound data

• Means of abstraction:

  • Procedure definition

  • Simple data abstraction

• Capturing common patterns

  • High-order procedures

  • Data as procedures

Suppose I want to express the general idea of a linear combination, which can be applied to various things such as:

• Numbers

• Vectors

• Polynomials

• Elecrtical signals

If our languages is good, it has to be able to express these general ideas, while also taking care of the fact that the underlying operations have to be performed differently depending on the specific type of data we have.

Somewhere in our system we have to put the knowledge of the kinds of things you can add, and on how you can add them together. Where do we put this knowledge? and how can we add new objects to our system without screwing up everything we already have and without adding too much code?

This is done by establishing conventional interfaces, which are agreed upon ways of connecting things together. In the course will see more in-depth the following ways of implementing such interfaces:

• Generic operators

• Large-scale structure and modularity

In general to build large-scale systems you can think about these two important metaphors:

• Object-oriented programming: you think of your system as a kind of society full of little things that interact with eachothers by sending messages.

• Operations on aggregates (streams): in this case the system is thought of as a series of signals.

Sometimes making a new language can help to manage the complexity of a particular domain.

We will start by analyzing the technology for building new computer languages, and we will express in LISP the process of interpreting LISP itself by the usage of two procedures: apply and eval, which constantly reduce expressions to eachothers.

We will also see the Y operator, which is sort-of the expression of infinity.

Then we will build a different kind of language, called logic programming language, where you don't talk about procedures, but rather about relations between things.

Finally, we'll talk how you implement this things very concretely.

LISP allows you to use the well known symbols such as '\(3\)', and '\(+\)', and '\(17.4\)' and so on.

Observation: The symbol '\(3\)' is not really the number "three", thats only some symbol that represents Plato concept of the number "three" in the same way that '+' is a symbol that represents the Plato's concept of how you add things.

So for example we can write the following (on the side commented is the output):

2    ;; 2
17.4 ;; 17.4
+    ;; #<procedure + (#:optional _ _ . _)>

We can put these primitive data together using the parentheses '\((\)' '\()\)' as follows

(+ 3 17.4 5)  ;; -> 25.4

This structure is called a combination. In general a combination consists in applying an operator, in this case the sum operator +, to some operands, in this case the numbers \(3\), \(17.4\), \(5\). Since the operands themselves can be combinations we can create more complex stuff

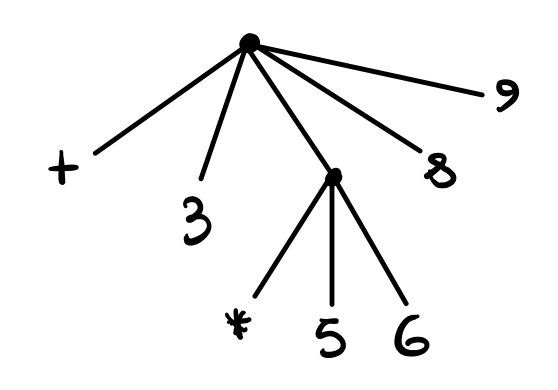
(+ 3 (* 5 6) 8 2)  ;; 43

LISP uses prefix notation, meaning that the operator is writtten to the left of the operands.

Finally, notice that parenthesis in LISP are very important to create combinations, since the usage of parenthesis makes the combination completely unambiguous. Another way to say this is that combinations can be visualized as trees, and parenthesis are a way to write out this two dimensional structure as a linear string of characters.

In LISP abstraction is obtained with the keyword define

(define A (* 5 5))
(* A A) ;; 625
(define B (+ A (* 5 A)))

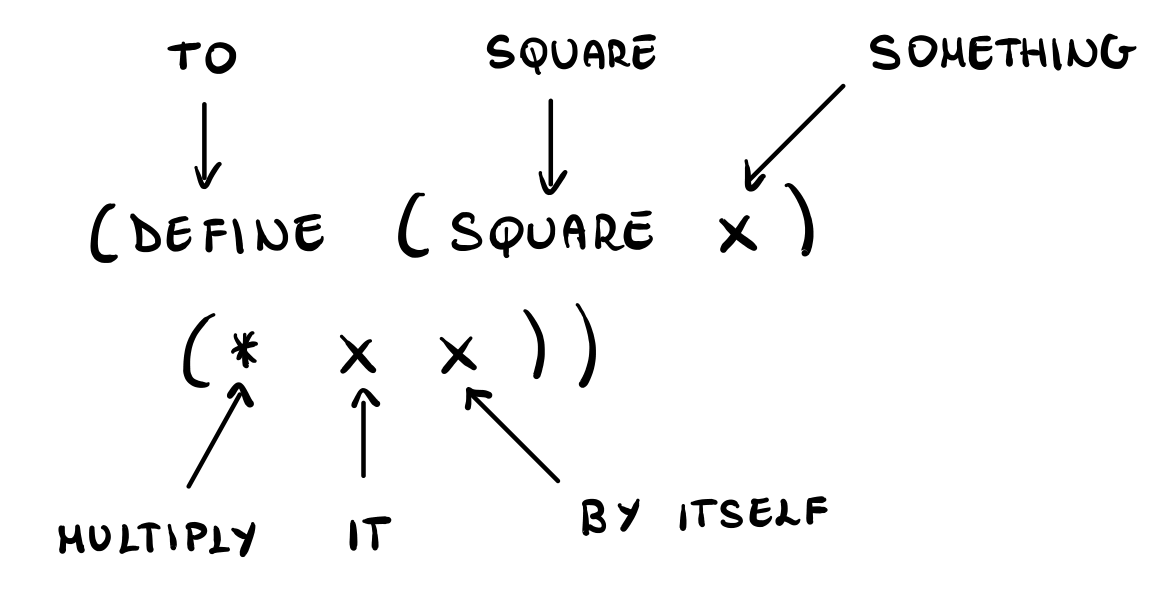
For example, suppose we want to express the general idea that we can multiply something by itself, that is, the idea of squaring. We can do this in LISP as follows

(define (square x) (* x x))
(square 10) ;; 100

Graphically,

An equivalent way of saying this is by using the keyword lambda, which allows one to define a nameless function.

(define square (lambda (x) (* x x)))

Graphically,

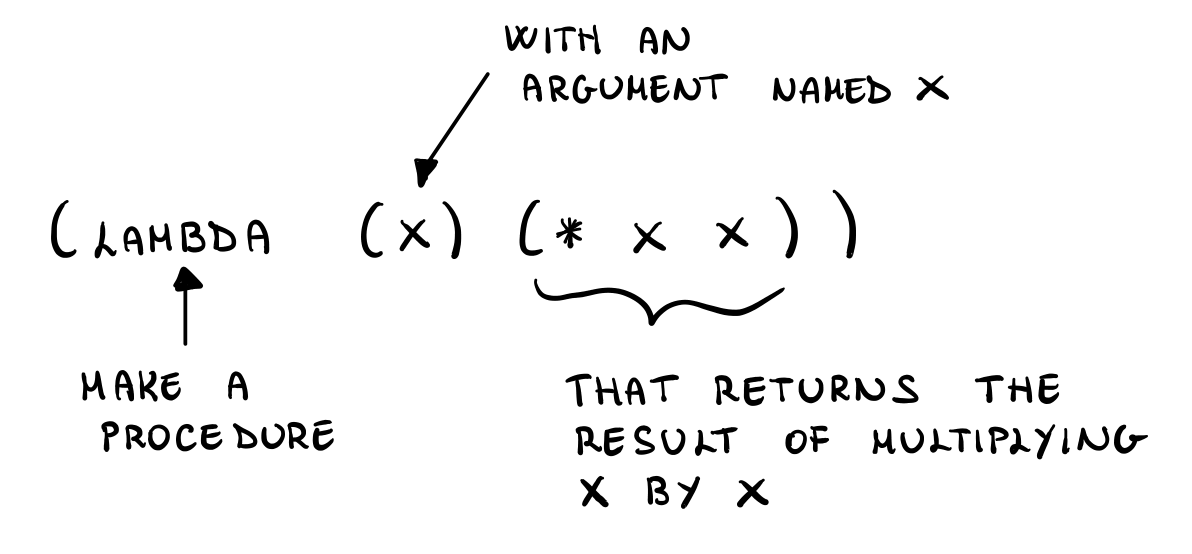
In general we'll mostly use the first form of define, because it is more convenient. Its important to stress out however that the two form whosn are equivalent for the LISP's interpreter. We say in this case that we have syntatic sugar, because we only have an easier way for typing something; the substance of the matter doesn't change.

Let now write two more procedures, one that compute the average between two numbers, and one that computes the average of the squares of the numbers:

(define (average x y)
  (/ (+ x y) 2))   

(define (mean-square x y)
  (average (square x)
           (square y)))

The key thing to note is that, now that we have defined the square procedure, we can use it as if it were a primitive like '+'. LISP doesn't make make arbitrary distinctions between things that happen to be primitive (built-in) in the language and things that happen to be compound.

(mean-square 2 3) ;; 6.5

In general for having a powerful abstraction mechanism you should not be able to tell the difference between built-in stuff and compound stuff.

To finish off or discussion about LISP, only one things need to be introduced: the cond keyword, used for case analysis, that is for situations in which we have to discriminate between a set of possible conditions.

Consider for example the absolute value function \(|x|\), which is defined as follows

\[|x| := \begin{cases} x \,\,&,\,\, x \geq 0 \\ -x \,\,&,\,\, x < 0 \\ \end{cases}\]

To compute such function in LISP we can write the following procedure

(define (abs x)
  (cond ((< x 0) (- x))
        ((= x 0) 0)
        ((> x 0) x)))

Notice that the cond statement has one or more clauses, where each clause is made up of a predicate and of an action.

It is often the case that you have a case analysis which has only a single case. For this a simplified version of cond is used

(define (abs x)
  (if (< x 0)
      (- x)
      x))

As was the case for the lambda and define keywords, in this case also the if and cond are essentially equivalent, and the only difference between them is some syntactic sugar.

These ideas are implement as follows:

(define (try guess x)
  (if (good-enough? guess x)
      guess
      (try (improve guess x) x)))

(define (sqrt x) (try 1 x)) 

Finally, we need to implement the sub-routines for good-enough? and improve . These can be implemented as such

(define (improve guess x)
  (average guess (/ x guess))

(define (good-enough? guess x)
  (< (abs (- (square guess) x))
     .001))

The program we built can be visualized as follows

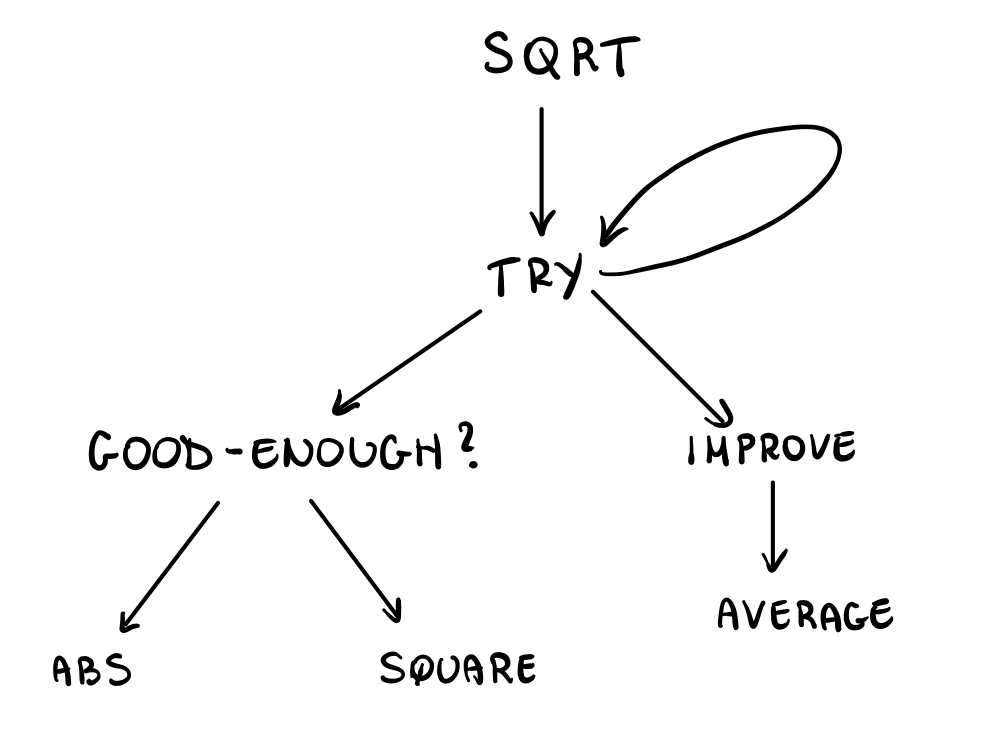
Notice that it is defined recursively, because we have defined try also in terms of itself.

Example of a computation

(sqrt 2)
(try 1 2)
(try (improve 1 2) 2)
(try (average 1 (/2 1) 2)
(try 1.5 2)
;; ...

We can build a square root box that contains all the necessary definitions in a so-called block structure as follows

(define (sqrt x)
  (define (improve guess)
    (average guess (/ x guess)))
  (define (good-enough? guess)
    (< (abs (- (square guess) x)) .001))
  (define (try guess)
    (if (good-enough? guess)
        guess
        (try (improve guess))))
  (try 1))