SICP - 02A - Higher Order Procedures

• Date: [2021-03-07 dom 18:00]

• Link: Lecture 2A | MIT 6.001 Structure and Interpretation, 1986

• Table of contents:

In this lecture we analyzed what it means to have "higher order procedures" and how we can use such procedures to implement useful abstractions.

The goal of this section is to write a procedure which abstracts the concept of a sum. Before actually doing that however let's consider the following particular sum

\[\sum_{i = a}^b i\]

To implement this particular sum we can write the following procedure

(define (sum-int a b)
  (if (> a b)
      0
      (+ a
         (sum-int (1+ a) b))))

Consider now this other sum

\[\sum_{i = a}^b i^2\]

To implement this other sum we can write the following

(define (sum-sq a b)
  (if (> a b)
      0
      (+ (square a)
         (sum-sq (1+ a) b))))

Finally, consider the following expression, which can be used to compute an approximation of \(\pi/8\)

\[\frac{\pi}{8} = \frac{1}{1 \cdot 3} + \frac{1}{5 \cdot 7} + \frac{1}{9 \cdot 11} + \ldots = \sum\limits_{i = 0}^{\infty} \frac{1}{(4i + 1)(4i + 3)}\]

We can implement it as follows

(define (pi-sum a b)
  (if (> a b)
      0
      (+ (/ 1
            (* (+ (* 4 a) 1)
               (+ (* 4 a) 3)))
         (pi-sum (1+ a) b))))

Notice that all the procedures we wrote so far are almost identical: their only difference is that in the first we sum at each step \(a\), in the second case we sum \(a^2\), and in the third \(1/(4a + 1)(4a + 3)\).

Now, when we program we typically shouldn't write same thing more than once. If we find ourselves writing time and time again code with the same structure, then we're probably missing some useful abstraction in our implementation, and we should do something about it.

In this particular case what we're missing is an abstraction that lets us talk about the general concept of a sum. Instead of having to write the same code everytime we have to implement a specific sum, we would like to write once a procedure which abstract the concept of a sum just like how the sigma notation lets us talk in mathematics about a general sum. Indeed, the power of the sigma notation in mathematics is that it allows us to reason about the concept of summation itself. When we write

\[\sum\limits_{n = a}^b f(n) = f(a) + \ldots + f(b)\]

we are talking about a general sum. Using this notation we can then prove general results about sums which apply to all possible sums we could make once we substitute specific values for the parameters \(a\), \(b\) and \(f(\cdot)\).

We want to do something like this, but in a program. This would give us a bunch of useful benefits. In terms of debugging, for example, with this approach we would only need to debug the general sum function once and then could use it as many times as we want for all the different sums we're interested in by simply calling the general procedure with different arguments.

The general pattern which covers all the case we have seen so far is the following

(define (<name> a b)
   (if (> a b)
       0
       (+ (<term> a)
          (<name> (<next> a) b))))  

where

• <name> is the name of the procedure which computes the sum.

• <term> is the name of the procedure which computes the term of the sum given the index of the element.

• <next> is the name of the procedure which computes the next index of the sum.

To implement this idea in a LISP procedure we would have to use a name to refer to a procedure and to pass this procedure to another procedure. So far we've only passed numbers to procedurs, and we never passed procedures themselves to procedures. However its crucial to note that numbers are not special. They are just a form of data; another form of data are procedures, and just as we can give names to variables that hold numbers, we can also give names to variables that hold procedures.

We thus get the following

(define (sum term a next b)
  (if (> a b)
      0
      (+ (term a)
         (sum term (next a) next b))))

And now we can write the previous procedures as instances of the more general sum procedure as follows

(define (sum-int a b)
  (define (identity a) a)
  (sum identity a 1+ b))

(define (sum-squares a b)
  (define (square a) (* a a))
  (sum square a 1+ b))

(define (pi-sum a b)
  (sum (lambda (i) (/ 1
                      (* (+ (* 4 i) 1)
                         (+ (* 4 i) 3))))
       a
       1+
       b))

With this approach we have abstracted the notion of a sum. Now in our program there is a clear separation between the general concept of a sum and the specific different sums we might want to do. This means that, if at any time we want to change the underlying implemention of the sum, all the other programs that use sum do not have to change.

For example we might want to have an iterative implementation of sum

(define (sum term a next b)
  (define (iter j ans)
    (if (> j b)
        ans
        (iter (next j)
              (+ (term j) ans))))
  (iter a 0))

But since we have written the programs by abstracting the notion of a sum, we do not have to change anything. We have created an abstraction barrier between the implementation of the sum procedure and how we use it.

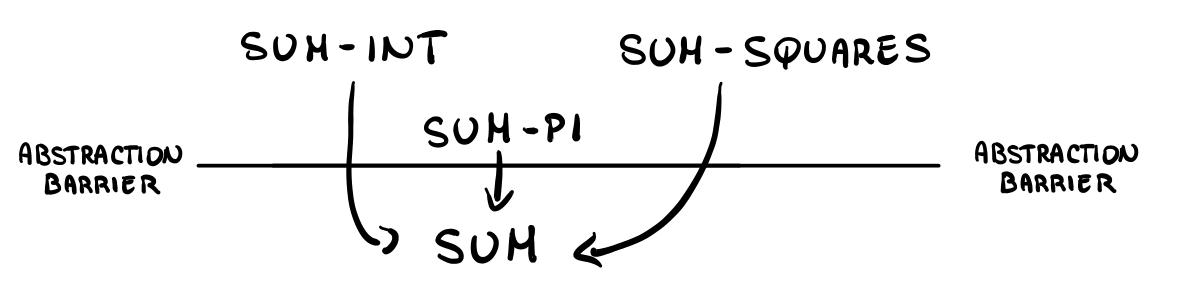
We call it a "barrier" because when we change the implemention of what is under the barrier we do not have to change the implementation of what is above the barrrier. The concept of abstraction barriers should be taken as a key takeway of this course, and will be mentioned many times in future lectures.

Consider the procedure we wrote for computing the square root in the first lecture.

(define (sqrt x)
  (define tolerance 0.0001)
  (define (good-enough? y)
    (< (abs (- (* y y) x)) tolerance))
  (define (improve y)
    (average (/x y) y))
  (define (try y)
    (if (good-enough? y)
        y
        (try (improve y))))
  (try 1))

Mathematically we have a procedure \(f(\cdot)\) for improving a guess for a square root.

\[f(y) = \frac{y + \frac{x}{y}}{2}\]

notice that \(f(\sqrt{x}) = \sqrt{x}\). Thus, to compute the square root of x we are looking for a fixed-point of the function \(f\), that is for a point \(y\) such that \(f(y) = y\).

Let us then try to abstract the concept of a searching for fixed-point of a function. We can explicitly express the idea that the square root of x is the fixed point of a given function with the following procedure

(define (sqrt x)
  (fixed-point
   (lambda (y) (average y (/ x y)))
   1))

To actually compute fixed-points we can use the following procedure, which simply keeps iteratevly applying the function to the value obtained so far until we find a value for which \(|f(y) - y| < \epsilon\) for a small value of \(\epsilon\).

(define (fixed-point f start)
  (define tolerance 0.0001)
  (define (good-enough? u v)
    (< (abs (- u v)) tolerance))
  (define (iter old new)
    (if (close-enough? old new)
        new
        (iter new (f new))))
  (iter start (f start)))

Notice that in our square root implementation we still have something to abstract, since in the current implementation we have hardcoded the particular function

\[f(y) = \frac{y +\frac{x}{y}}{2}\]

and there are other functions whose fixed point are square roots. For example we could simply use the easier function

\[g(y) = \frac{x}{y}\]

Notice that if \(y\) is a fixed-point of \(g(\cdot)\), then

\[g(y) = x/y = y \iff y^2 = x \iff y = \pm \sqrt{x}\]

and thus \(y\) is the square root of \(x\). The problem with using this function is that it oscillates. That is, if we applying \(g(\cdot)\) to itself we go back and forth between two values as is shown below

\[g(g(y)) = g\Big(\frac{x}{y}\Big) = \frac{x}{\frac{x}{y}} = \frac{x}{1} \cdot \frac{y}{x} = y\]

That is why we use the function \(f(\cdot)\): because it is the average between \(y\) and \(g(y)\). By averaring \(g(y)\), we dump out the oscillations in such a way that allows us to converge to our fixed-point.

By implementing all this ideas we can write our square root in an even clearer way as follows

(define (sqrt x)
  (fixed-point
   (average-damp (lambda (y) (/ x y)))
   1))

Where average-damp is a special procedure that takes in input a procedure and produces as output another procedure. This is the first time we see a procedure being produced as output. The procedure can be implemented in various ways, as is shown below

(define average-damp
  (lambda (f)
    (lambda (x) (average (f x) x))))


(define (average-damp f)
  (lambda (x) (average (f x) x)))

(define (average-damp f)
  (define (foo x)
    (average (f x) x))
  foo)

Procedures like average-dump , that is procedures which take in input other procedures and that produce as output other procedures, are called higher-order procedures.

Newton's Method is a method used to find the roots of functions.

It works as follows: to find a \(y\) such that \(f(y) = 0\) we start with some initial guess \(y_0\), and then we iterate the following function until we find a fixed-point.

\[y_{n+1} = y_n - \frac{f(y_n)}{\displaystyle{\frac{df}{dy} (y_n)}}\]

The method can be implemented as follows

(define (netwon f guess)
  (define df (deriv f))
  (fixed-point
   (lambda (x) (- x (/ (f x) (df x))))
   guess))

Let us now apply Netwon's Method to compute our square root.

If we define

\[f(y) = y^2 - x\]

then by finding the root of such equation we find a \(y\) such that

\[-x + y^2 = 0 \implies y^2 = x\]

that is, \(y\) is the square root of \(x\). Our procedure can then be written in the following way

(define (sqrt x)
  (netwon (lambda (y) (- x (square y)))
          1))

Let us now take a look at what we've done. To compute the square root \(\sqrt{x}\) of a given number \(x\) we have constructed the following box.

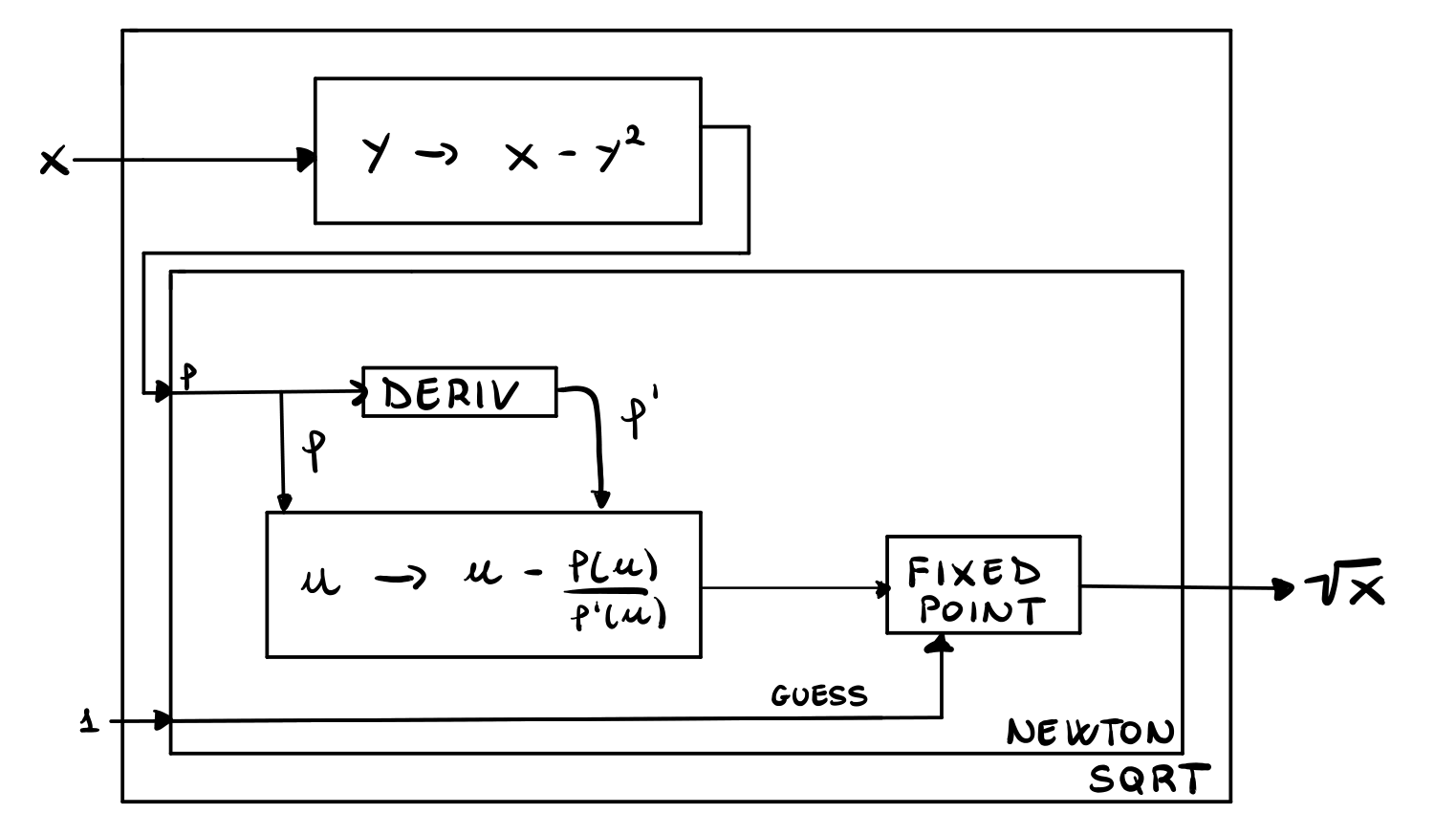
Its crucial to realize that within this box there are independent components, like the module for computing the fixed-point, which can also be used for other computation thanks to the abstractions we have set in place. This construction was possible because procedures in the scheme programming language are so-called first-class citizens. In a programming context, an entity is said to be first-class if it can do the following things:

• Be named by variables.

• Be passed as arguments to procedures.

• Be returned as values of procedures.

• Be incorporated into data structures.