SICP 02B - Data Abstraction
Lecture Info
Date:
Link: Lecture 2B | MIT 6.001 Structure and Interpretation, 1986
Table of contents:
In this lecture we talked about abstraction barriers in terms of data by implementing a system for doing arithmetic with rational numbers. The concept of data abstraction was introduced and at the end we saw the first signs that in LISP the line between data and procedures is very blurred.
1 Abstraction Barriers for Data
When we're building things we want to divorce the task of building things from the task of implementing the parts. This is done by creating abstract barriers. In the previous lecture we used the concept of high-order procedures to implement procedural abstract barriers. We will now look at the same issues but this time for data. In particular we will see the following things:
Primitive data
Means of combinations for data
Means of abstraction for data
The key aspect in all of this, once again, is that we will construct a system by layering abstraction barriers together.
2 Rational Arithmetic
Let us now understand how we would implement in LISP a system that does arithmetic on rational numbers. That is, we want a system that could answer the following questions
\[\begin{split} \frac12 - \frac14 = \frac34 \\ \\ \frac34 + \frac23 = \frac12 \\ \end{split}\]
Remember that when dealing with fractions we use the following formulas:
\[\begin{split} \frac{n_1}{d_1} + \frac{n_2}{d_2} &= \frac{n_1 \cdot d_2 + n_1 \cdot d_1}{d_1 \cdot d_2} \\ \\ \frac{n_1}{d_1} \cdot \frac{n_2}{d_2} &= \frac{n_1 \cdot n_2}{d_1 \cdot d_2} \\ \end{split}\]
The only problem we have in implementing such system is that by using traditional LISP we don't know what a rational number actually is. That is, our system only gives us individual numbers, like \(3\) and \(5\), but it doesn't have a way of saying what is \(3/5\) for example.
2.1 Constructor and Selectors
To solve this problem we'll use the usual strategy of wishful thinking, that is we assume that we have the following three produces:
(make-rat n d), which returns a "cloud" that represents the rational number \(n/d\).
(numer "cloud n/d"), which, given a "cloud" that represents the rational number \(n/d\), returns the numerator \(n\).
(denom "cloud n/d"), which given a "cloud" that represents the rational number \(n/d\), returns the denominator \(d\).
Notice the difference between the first procedure and the other two:
make-rat is used to create the abstract cloud which will be our
abstract representation of a rational number, while numer and denom
are used to get inside the abstract cloud and extract the actual
data. To signal this difference we say that make-rat is a
constructor, while numer and denom are selectors.
2.2 Basic Operations
With these produces its easy to implement the basic operation between rational numbers:
(define (+rat x y) (make-rat (+ (* (numer x)(denom y)) (* (numer y)(denom x))) (* (denom x) (denom y))))
(define (*rat x y) (make-rat (* (numer x) (numer y)) (* (denom x) (denom y))))
Let us now understand why we would want to use procedures like
+rat . The idea is that while it is true that we can represent a
single fraction with just two numbers, as soon as we have to
combine fractional numbers in complex operations such as
\[(x + y) \cdot (s + t)\]
where \(x, y, s, t\) are fractional numbers, then if we didn't have
+rat we would have to worry about a lor of temporray variables,
which would confuse the mind of the programmer. Since we have +rat
we can simply write
(*rat (+rat x y)( +rat s t))
Never forget that our programming languages should let us be able to express the concepts we have in our minds. Its the language that should get closer to our mind, and not viceversa.
2.3 List structure in LISP
To construct our rational numer system so far we have broken down the problem into two parts:
How do we implement basic rational operations given a way to construct a compound data representing a single fractional value? That is, how do we manipulate compound data representing ractional values?
How do we construct the compound data itself?
Let us now solve the second problem, that is, let us understand how can we "glue" together the denominator and the nominator to form a single data object. Each language in the LISP family provides such a glue by using the so-called list structure, which consist in a primitive to construct pairs of values and two other primitives to extract each value from the pair. These primitives are described as follows:
(cons x y), constructs a pair whose first part is x and whose second part is y.
(car p), given a pair p selects the first element of the pair.
(cdr p), given a pair p selects the second element of the pair.
There is also a conventional way of drawing pictures of these things called box and pointer notation.
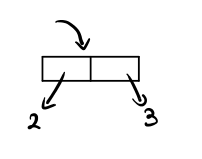
Notice that, for any x and y, we have that
(car (cons x y)) -> x (cdr (cons x y)) -> y
Given such operations, its pretty clear how we can represent our rational numbers
(define (make-rat n d) (cons n d)) (define (numer x) (car x)) (define (denom x) (cdr x))
2.4 Usage
Now that we have a complete implementation of our rational number system, let us see some exmaples
;; compute 1/2 + 1/4 (define A (make-rat 1 2)) (define B (make-rat 1 4)) (define ans (+rat A B)) (numer ans) ;; 6 (denom ans) ;; 8
Notice that instead of giving us \(3/4\), the system gives us
\(6/8\). This happens because in our current implementation our
system never reduces the fractions it works with to their lowest
terms. If we are interested in reducing our fraction to their
lowest term we can implement this functionality in the make-rat
procedure as follows
(define (make-rat n d) (let ((g (gcd n d))) (cons (/ n g) (/ d g))))
where gcd computes the greatest common divisor between n and d
using the euclidean algorithm.
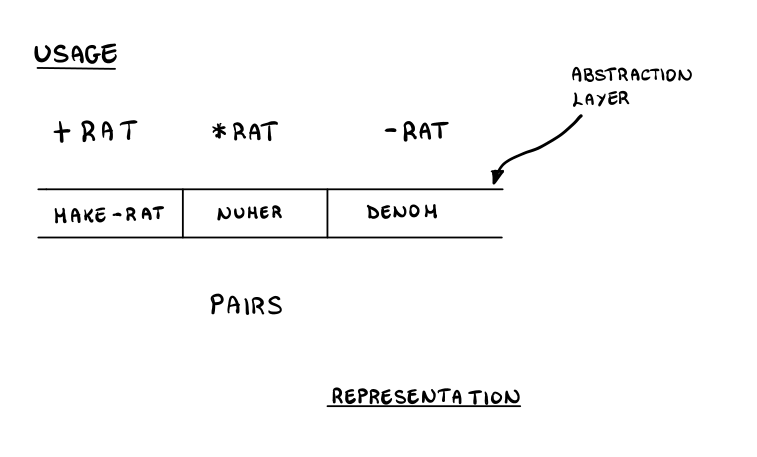
2.5 Data Abstraction
In the scheme we have implemented, between the operation on
rational numbers such as *rat , +rat , -rat , etc, and the underlying
data structure, which in this case was the basic pair , we have set
up an abstraction barrier which was made up of the constructor
make-rat and the two selectors numer , denom . That is, we have
separated clearly the use of data object from the representation of
data objects. This methodology is called data abstraction and its a
very important tool in building complex systems.
We are not forced to use data abstraction. For example we could've implemented our sum of rational numbers without abstracting as follows
(define (+rat x y) (cons (+ (* (car x) (cdr y)) (* (car y) (cdr x))) (* (cdr x) (cdr y))))
This approach however is not ideal because of naming: in such a procedure we never have the idea of a rational number as a conceptual entitiy on its own. That is, we cannot point our finger to a rational number in there. A big advantage of instead abstracting the idea of a rational number is that we could create different representations for a rational number. For example we could create a different representation in which instead of computing the gcd when we create fractions we might want to compute it when we extract the numerator/denominator. Since a given representation is only good in certain contexts and under certain requirements, having multiple representation would allow our system to be more flexible.
In general, as system designers, the way one should retain flexibility is to never make up your mind about anything until you're forced to do it. Unfortunately, there is a very narrow line between deferring decisions and outright procrastinating. The ideal is thus to make progress, and yet not being constrainted by the consequences of decisions made. Data abstraction is one way of doing this.
Observation 1: Computer science is like magic, but the bad parts of computer science are a lot like religion. In general people who really believe that you should design everything before you implement it basically are people who have never worked on a complex system. The real power is that you can pretend that you have made a decision, and then later one figure out which one is right, that is which decision you ought to have made.
Observation 2: When you do (define A 5) you set up a value for A in the global context. When instead you use let you are creating a context in which you can make local definitions.
(let ((z 10))
(+ z z))
3 Geometric Entities
When someone shows you a method for controlling complexity you really need to ask yourself:
what can I do with it?
Suppose we want to represent points in a plane such as the point \(P = (1, 2)\). To represent such points we could define the following procedures
(define (make-vector x y) (cons x y)) ;; constructor (define (xcor p) (car p)) ;; selector (define (ycor p) (cdr p)) ;; selector
Given two points in a plane \(P=(1, 2)\), \(Q=(2, 3)\) we could then talk about the line segments between these two points. To represent such segment we could use the same construction as before
(define (make-seg p q) (cons p q)) (define (seg-start s) (car s)) (define (seg-end s) (cdr s))
We can then define some operation on such segments. For example, to compute the mindpoints of a line segment we could do the following
(define (midpoint s) (let ((a (seg-start s)) (b (seg-end s))) (make-vector (average (xcor a) (xcor b)) (average (ycor a) (ycor b)))))
Similarly we can talk about the length of a segment as follows
(define (length s) (let ((dx (- (xcor (seg-end s)) (xcor (seg-start s)))) (dy (- (ycor (seg-end s)) (ycor (seg-start s))))) (sqrt (+ (square dx) (square dy)))))
Once again, we have a layered system, which can be visualized as follows:
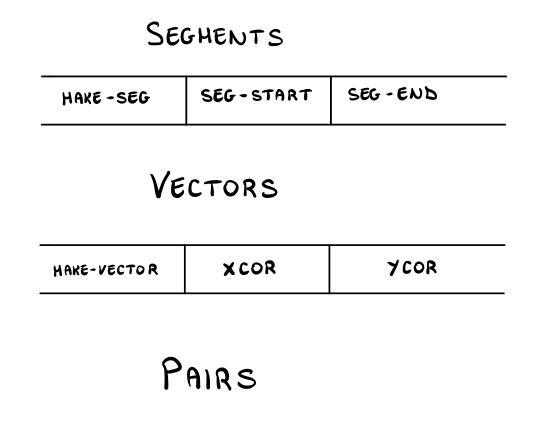
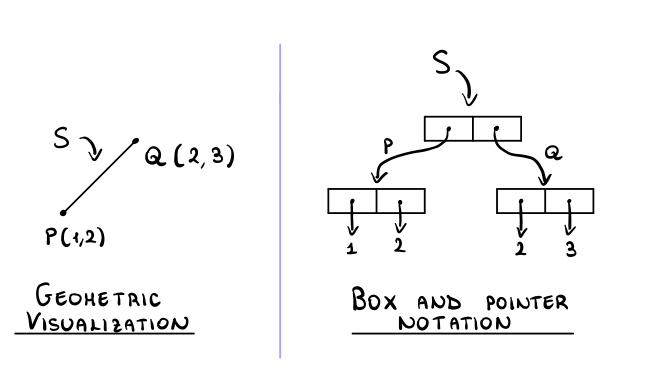
A visual representation of a segment is then the following one.
Notice that if you do not use astraction barriers it is very easy to get lost in the complexity. For example for the length of a segment we get
(define (length s) (let ((dx (- (car (car s)) (car (car s)))) (dy (- (cdr (cdr s)) (cdr (cdr s))))) ; ....))
Also, without abstraction barriers whenever we change the way we represent a line segment we'd also have to change all this code. We have solved this problem by being explicit about the means of representations. And by being explicit about them, by giving them names, we gain control over them.
4 Closure
The power of using cons in all the constructions we have seen so far
is that with cons we can put things together into pairs, and these
pairs can be themselves part of other pairs. To describe this
behaior of cons we talk about closure, by which we mean that the
means of combinations in your system are such that, when you put
things together using them, you can then put the results together
with the same means of combinations. That is, we can not only have a
pair of numbers, but also a pair of pairs.
As a counterexample, making an array in Fortran is not a closed means of combination, because I can make an array of numbers, but I cannot make an array of arrays. One of your test of quality for testing a means of combination is:
Are the things you make closed under that means of combination?
In LISP we can make pairs of pairs, and that means we can build anything we want.
"Once you have two things you have as many things as you want." cit. Harold Abelson.
5 Abstract Data
So far we have seen a couple example of data abstraction. Let us now understand what we mean when we talk about data. That is, let us ask this question: what is data?
"In computer programming its always much harder to talk about what something means than to go and do it", cit. Harold Abelson.
Remember what we did at the start of this lecture, when we
implemented the rational number operations in terms of the
prodecures make-rat , enum , denom . What we did exactly was defining
our operations in terms of abstract data. When we defined such
operations, any implementations could then be used for representing
the underlying data unit, which in our case had to represent a
rational number.
Notice however that not all possible implementation of these three procedures make sense. Indeed, most of them wont. But, among all the procedures, there are some that do make sense for our purposes. That is, there are some procedures that can be used to represent rational numbers. How then do we discriminate between these "suitable procedures" and the procedures which are totally meaningless in this context?
To answer this we can reason in a sort of axiomatic way as follows:
let x be the result of the procedure call (make-rat n d) . Then, for
our set of procedures to be suitable, we would want the following
(numer x) = n(denom x) = d
That is,
\[\frac{(\text{numer } x)}{(\text{denom } x)} = \frac{n}{d}\]
This is the contract that has to be followed for a representation to be suitable for representing rational numbers. We don't particular care how this contract is respected, we only care that it is.
5.1 Pairs in terms of Procedures
Let's keep digging. What is a rational number representation?
Previously we have implemented them using pairs, and since such
implementation correctly followed the contract, we can indeed say
that thats a possible implementation. But then, what are pairs?
Once again, we used an axiomatic approach, and we defined pairs to
be structures and for any x and y
(car (cons x y)) ---> x (cdr (cons x y)) ---> y
Let us now see how we might build a pair using a procedure.
(define (cons a b) (lambda (pick) (cond ((= pick 1) a) ((= pick 2) b)))) (define (car x) (x 1)) (define (cdr x) (x 2))
Notice that in such definitions we don't see any data in there, but
only a procedure. That is, (cons a b) returns a procedure that
returns either the first or second element, depending on the input
argument.
To show that such an implementation is a correct representations of a pair then we just have to show that the axioms are respected. We can do this by using the substituion model as follows.
(car (cons 37 49))
(car (lambda (pick)
(cond ((= pick 1) 37)
((= pick 2) 49))))
((lambda (pick)
(cond ((= pick 1) 37)
((= pick 2) 49)))
1)
(cond ((= 1 1) 37)
((= 1 2) 49))
37
since this implementation satisfies the axioms, we can build pairs using procedures. And since pairs can then be used to build any other data, it means that all data could be built using only procedures.
Observation: For pratical purposes, to increase the efficiency of
the system in scheme there is actually a primitive called cons
which constructs primitive data. Still, the point we reaisedr
remains valid since, theoretically, cons could be implemented as we
have shown, and it wouldn't make any different at all to the system
(other than possibly performance wise). Thus, the takeway is that
in some sense we don't need any data at all to build these data
abstractions, since we could make everything with procedures.
The takeaway of this lesson is that in some programming languages such as LISP, the line between data and procedures can be very blurry. A lot of programming techniques we will see in the course depend very crucially on blurring this traditional line between data and procedures.
In our language procedures are objects. They are not merely the "act of doing something". A procedure is a real object that has an existence.