SICP 04B - Generic Operators
Lecture Info
Date:
Link: Lecture 4B | MIT 6.001 Structure and Interpretation, 1986
Table of contents:
In this lecture we discussed the concept of generic operators, we saw two different ways to implement them and we saw how to use generic operators to implement a generic arithmetic system.
1 Vertical Abtraction Barriers
So far we have seen many examples of abstraction barriers that separates the way some data is used from the way it is represented.
While this notion of data abstraction is really powerful, it is not really sufficient for building complex systems, because in such systems it is typically the case that many different people offer many different implementations. We would thus like to have some sort of "vertical barriers" as well as the horizontal ones we have already seen.
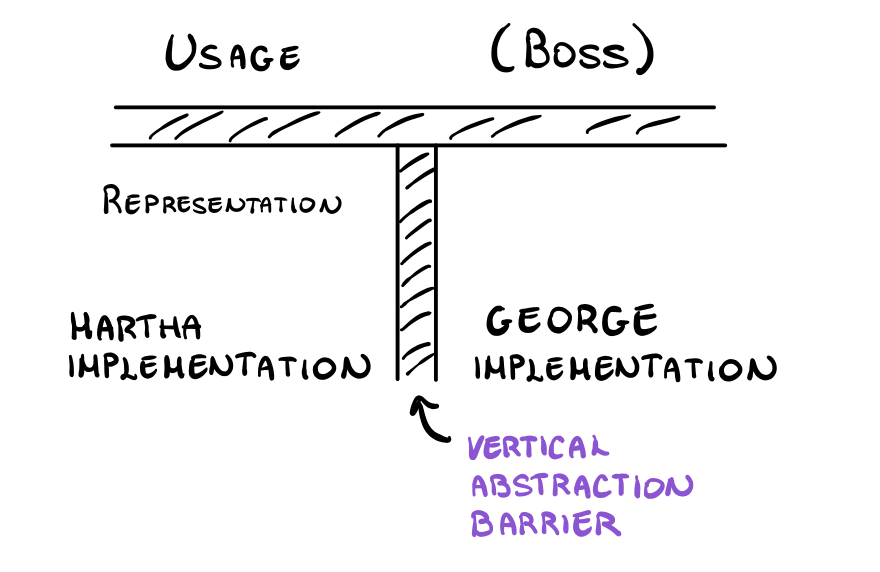
Consider for examle the problem of managing personal records of a company that is formed by many different companies, each of which has its own representation of a personal record. We would like to be able to extract from these records various informations such as the name, the salary, the job, and so on, without having to worry about the fact that each division has completely separate conventions for how to implement these records.
Other than the simplest solution of telling all the division to
stick to a conventional format, which usually doesnt work, one could
reason as follows: we want to implement a procedure name to be a
so-called generic operator, meaning that what it does depends on the
kind of data its looking at. Our system then has to be able to
support future divisions by making minimal changes to the codebase.
Instead of tackling this distributed personal records problem, let us instead introduce the concept of generic operators in a more "traditional" mathematical problem: doing arithmetic on complex numbers.
2 Arithmetic on complex numbers
As a little review, a complex number is a point in the plane which can be represented by its imaginary part and its real part using the traditional cartesian coordinates, or by using the poolar coordinates, which instead specify a point by using the distance from the origin and the angle.
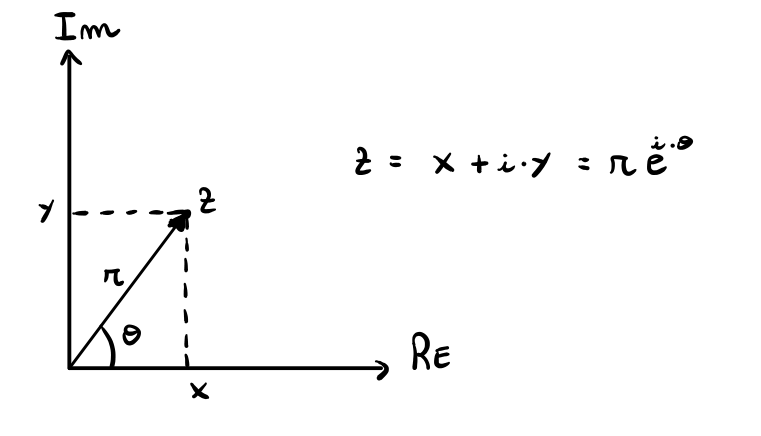
To go between one representation to another the following equations can be used
\[\begin{split} x &= r \cdot \cos{(\theta)} \;\;\;\;\;\;\;\;\; r &= \sqrt{x^2 + y^2}\\ y &= r \cdot \sin{(\theta)} \;\;\;\;\;\;\;\;\; \theta &= \arctan{\Big(\frac{y}{x}\Big)}\\ \end{split}\]
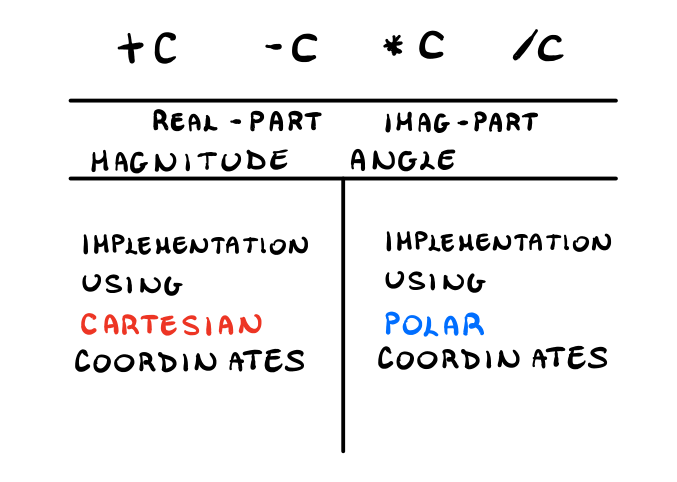
We would thus like to define these operators that operate on two complex numbers to sum, subtract, multiply and divide them.
(define (+c z1 z2) ;; ... ) (define (-c z1 z2) ;; ... ) (define (*c z1 z2) ;; ... ) (define (/c z1 z2) ;; ... )
The math formulas for implementing such things are described as follows
\[\begin{split} \text{Re}(z_1 + z_2) = \text{Re}(z_1) + \text{Re}(z_2) \\ \text{Im}(z_1 + z_2) = \text{Im}(z_1) + \text{Im}(z_2) \\ \\ \text{Mag}(z_1 \cdot z_2) = \text{Mag}(z_1) \cdot \text{Mag}(z_2) \\ \text{Angle}(z_1 \cdot z_2) = \text{Angle}(z_1) + \text{Angle}(z_2) \\ \end{split}\]
2.1 Operations
As far as the representation is concerned, we can assume to have the following:
Constructors:
(make-rectangular x y) (make-polar r a)
Selectors
(real-part z) (imag-part z) (magnitude z) (angle z)
This means that we can implement the previous math formula in lisp as follows
(define (+c z1 z2) (make-rectangular (+ (real-part z1) (real-part z2)) (+ (imag-part z1) (imag-part z2)))) (define (-c z1 z2) (make-rectangular (- (real-part z1) (real-part z2)) (- (imag-part z1) (imag-part z2)))) (define (*c z1 z2) (make-polar (* (magnitude z1) (magnitude z2)) (+ (angle z1) (angle z2)))) (define (/c z1 z2) (make-polar (/ (magnitude z1) (magnitude z2)) (- (angle z1) (angle z2))))
As we can see, when we add or subtract two complex numbers we represent the resulting complex number using cartesian coordinates, and when we multiply or divide them we use the poolar cordinates instead.
2.2 Representation
2.2.1 With cartesian coordinates
The actual implementation of the complex numbers can be done first as pairs of cartesian coordinates as follows
;; Cartesian coordinates ;; -- constructor (define (make-rectangular x y) (cons x y)) ;; -- selectors (define (real-part z) (car z)) (define (imag-part z) (cdr z)) ;; Poolar coordinates ;; -- constructor (define (make-polar r a) (cons (* r (cos a)) (* r (sin a)))) ; -- selectors (define (magnitude z) (sqrt (+ (square (car z)) (square (cdr z))))) (define (angle z) (atan (/ (cdr z) (car z))))
Conceptually what we've done so far is exactly the same as what we did for representing rational numbers. As we can see, anytime we have to create a complex numbers using polar coordinates we have to do some intermediate work to get the respective cartesian coordinates.
2.2.2 With polar coordinates
Consider now a different representation of complex numbers, using pairs of magnitude and angle.
;; Polar coordinates ;; -- constructor (define (make-polar r a) (cons r a)) ;; -- selectors (define (magnitude z) (car z)) (define (angle z) (cdr z)) ;; Cartesian coordinates ;; -- constructor (define (make-rectangular x y) (cons (sqrt (+ (square x) (square y))) (atan (/ y x)))) ;; -- selectors (define (real-part z) (* (car z) (cos (cdr z)))) (define (imag-part z) (* (car z) (sin (cdr z))))
2.2.3 Which is better?
So then, one could ask, which idea is better? Well such question has no definite answer, as the answer varies depending on what you want to do with such numbers:
If you do more additions/subtractions, the first idea is better.
If you do more products/divisions, the second idea is better.
In general though the key takeway here is that we cannot decide
which representation is better. This is why we we would like a
system in which both representation can co-exist, and the various
operatiors +c , -c , *c , /c , are generic operators that depending on
the particular representation behave differently.
2.3 Typed Data
One idea to support both kind of representation is to introduce the notion of what is called typed data, that is data which contains both a content and a type. We can easily add this information by using cons as follows
(define (attach-type type contents) (cons type contents)) (define (type datum) (car datum)) (define (contents datum) (cdr datum))
We can then have some type predicates to understand the type of a
given datum .
(define (rectangular? z) (eq? (type z) 'rectangular)) (define (polar? z) (eq? (type z) 'polar))
Consider then John, the author of the first kind of representation (the one using rectangular coordinates). To make a rectangular package he has to change his code as follows
(define (make-rectangular x y) (attach-type 'rectangular (cons x y))) (define (real-part-rectangular z) (car z)) (define (imag-part-rectangular z) (cdr z)) (define (magnitued-rectangular z) (sqrt (+ (square (car z)) (square (cdr z))))) (define (angle-rectangular z) (atan (/ (cdr z) (car z))))
Notice that the real-part procedure has to change name, becauase
both John and Martha have a procedure named like that. Thus, for
these procedure to coexist in the same LISP environment, the name
has to be changed to real-part-rectangular , where rectangular
defines the name for the package, which is assumed to be unique.
Martha has to do the same thing as John of course
(define (make-polar r a) (attach-type 'polar (cons r a))) (define (real-part-polar z) (* (car z) (cos (cdr z)))) (define (imag-part-polar z) (* (car z) (sin (cdr z)))) (define (magnitude-polar z) (car z)) (define (angle-polar z) (cdr z))
We then have a bunch of generic selectors for complex numbers
operations, which execute the particular operation depending on the
data.
(define (real-part z) (cond ((rectangular? z) ;; .... ) ((polar? z) ;; ... ))) ;; .... (define (angle z) (cond ((rectangular? z) ;; .... ) ((polar? z) ;; ... )))
Let's look more closely at the first one
(define (real-part z) (cond ((rectangular? z) (real-part-rectangular (contents z))) ((polar? z) (real-part-polar (contents z)))))
3 How to Implement Generic Operators
There are many different ways to implement generic operators. We will two in particular:
Dispatch on type.
Data directed programming.
3.1 Dispatch on Type
This stragey that we have just used for implementing complex arithmetic is called dispatch on type, and the basic idea is that you break your system in a bunch of pieces and than there's the manager who looks at the type of data and dispatches it at the right person.
What can we complain about such organization?
Both john and martha had to change their procedures names. This problem can be solved by using LISP's namespace capabilities, which we will not look at right now;
The problem is that when you bring somebody new you have to change all of the procecures of the manager. This means that the inflexibility of the system, that is where work has to happen to accomodate change, is in the manager.
Abstractlly in our system there is the following table
\[\begin{array}{c | c | c} & \textbf{polar} & \textbf{rect}\\ \hline \textbf{real-part} & \text{real-part-polar} & \text{real-part-rectangular} \\ \textbf{image-part} & \text{image-part-polar} & \text{image-part-rectangular} \\ \vdots & \\ \end{array}\]
3.2 Data Directed Programming
To improve our system the idea is to throw away the manager and automate the looking up process by using directly the table itself. Assume in particular we have a table that can be used with the following procedures
;; stores in the table the given value under the ;; given keys (put key1 key2 value) ;; retrieves the value associated with key1, key2 (get key1 key2)
Given this organization, when John and Martha add their representations to the system they have the responsibility to set up their appropriate rows in the table. For example John has to do the following
(put 'rectangular 'real-part
real-part-rectangular)
(put 'rectangular 'imag-part
imag-part-rectangular)
;; ...
While Martha does the following
(put 'polar 'real-part
real-part-polar)
(put 'polar 'imag-part
imag-part-polar)
;; ...
The manager now is replaced by a procedure called operate , which
takes in input an operation op and an object obj on which to
perform such operation.
(define (operate op obj) (let ((proc (get (type obj) op))) (if (not (null? proc)) (proc (contents obj)) (ERROR "undefined OP"))))
We then use the operator to define the various selectors
(define (real-part obj) (operate 'real-part obj)) (define (image-part obj) (operate 'image-part obj)) (define (magnitude obj) (operate 'magnitude obj)) (define (angle obj) (operate 'angle obj))
Let us see an example, where we assume that \(z\) is a complex number implemented using polar coordinates.
;; assume z -> '(polar ( 1 2)) (real-part z) (operate 'real-part z) ((get 'polar 'real-part) (contentz z)) (real-part-polar '(1 2))
This is another, more flexible approach for implementing generic operators, and its called data directed programming. The idea of such approach is that the data objects themselves are carrying around the information on how you should operate with them.
If in the data you also memorize the operations themselves, then we get another way to organize our system called message passing.
4 Generic Arithmetic System
The power of the methodology we have just described comes out when
we embed our system in a more complex system. Let's assume that we
have a generic arithmetic system, where we can do like add , sub , and
so on.
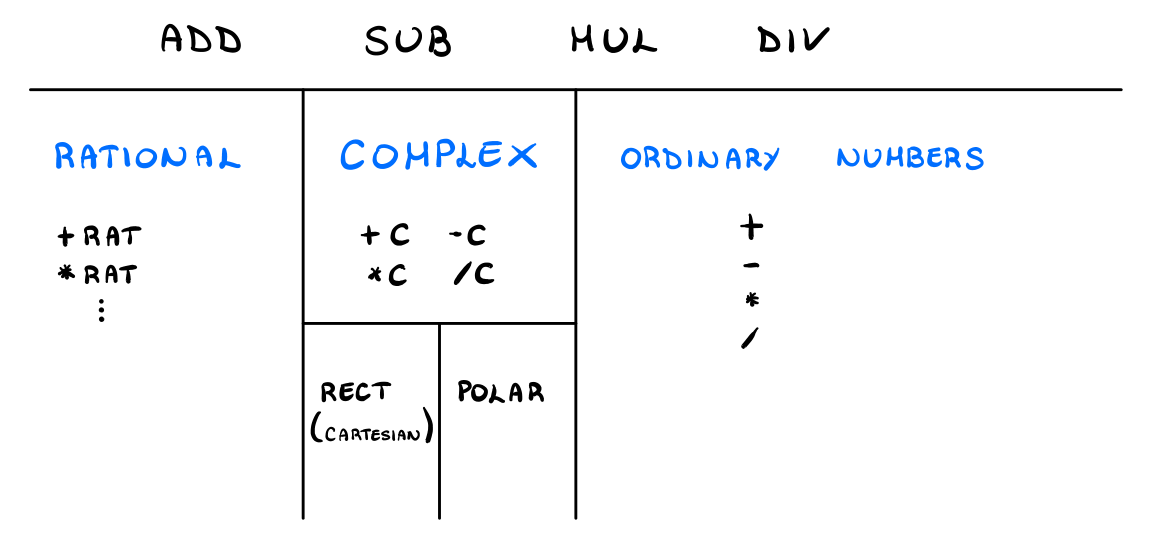
4.1 Rational Numbers
To install our rational number system that we have implemented in a previous lecture in this more generic arithmetic system we can do the following
(define (make-rat x y) (attach-type 'rational (cons x y))) (put 'rational 'add +rat) (put 'rational 'sub +rat) (put 'rational 'mul *rat) (put 'rational 'div /rat)
Let us now define these generic operators
(define (add x y) (operate-2 'add x y))
where operate-2 is defined as follows
(define (operate-2 op arg1 arg2) (if (eq? (type arg1) (type arg2)) (let ((proc (get (type arg1) op))) (if (not (null? proc)) (proc (contents arg1) (contents arg2)) (error "Op undefined on type"))) (error "Args not same type")))
4.2 Complex numbers
To instead install our complex numbers we do the following
(define (make-complex z) (attach-type 'complex z)) (define (+complex z1 z2) (make-complex (+c z1 z2))) (put 'complex 'add +complex) ;; Similarily for the other operations
4.3 Ordinary Numbers
Finally, to install ordinary numbers we do the following
(define (make-number n) (attach-type 'number n)) (define (+number x y) (make-number (+ x y))) (put 'number 'add +number) ;; Similarly for the other operations
The scheme we have now is the following
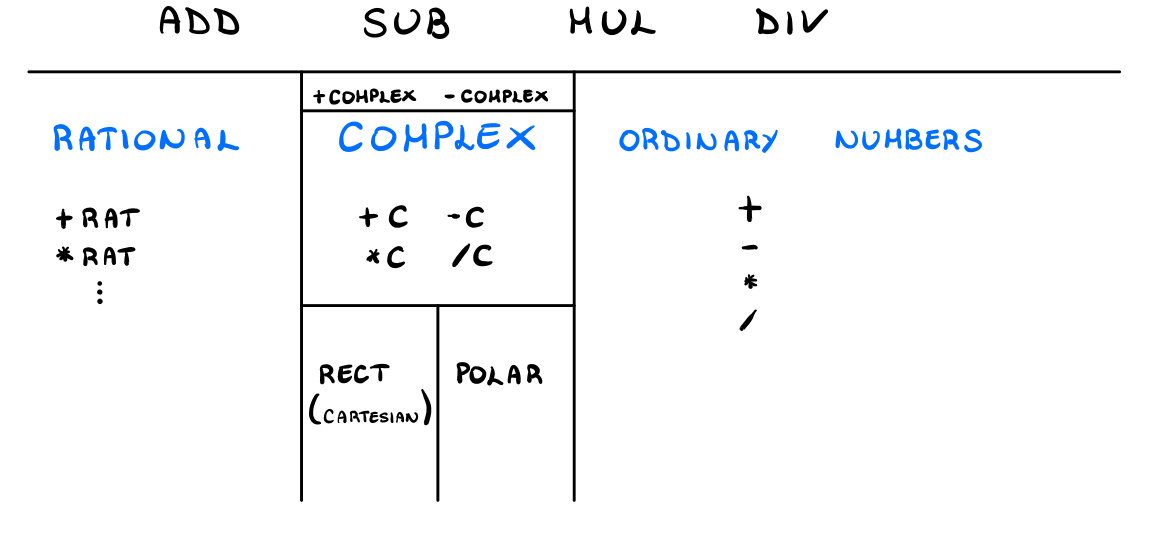
4.4 Example
Suppose we want to multiply two complex numbers such as
\[(3 + 4i) \cdot (2 + 6i)\]
Notice we have these chains of types, and anytime we have some ambiguity about where to go under the horizontal line, the type is telling you where to go.
4.5 Polynomials
Let's make this system even more complex by adding support for polynomials. A polynomial is a typed object which can be represented as follows
(polynomial x <term list>)
where the
((15 1) (7 2) (0 5) ... (<order>, <coefficient>))
That is, we have the following representation
\[\begin{split} x^{15} + 2x^7 + 5 &\longrightarrow \text{(polynomial x ((15 1) (7 2) (0 5))} \\ y^{15} + 2y^7 + 5 &\longrightarrow \text{(polynomial y ((15 1) (7 2) (0 5))} \\ z^3 + z^2 + z &\longrightarrow \text{(polynomial z ((3 1) (2 1) (1 1))} \\ \end{split}\]
To implement our polynomial arithmetic we proceed as follows
(define (make-polynomial var term-list) (attach-type 'polynomial (cons var term-list))) (define (+poly p1 p2) (if (same-var? (var p1) (var p2)) (make-polynomial (var p1) (+terms (term-list p1) (term-list p2))) (error "Polys not in same var"))) (put 'polynomial 'add +poly)
Where two term-lists are added as follows
(define (+terms l1 l2) (cond ((empty-termlist? l1) l2) ((empty-termlist? l2) l1) (else (let ((t1 (first-term l1)) (t2 (first-term l2))) (cond ((> (order t1) (order t2)) (adjoin-term t1 (+terms (rest-terms l1) l2)) ((< (order t1) (order t2)) (adjoin-term t2 (+terms l1 (rest-terms l2)))) (else (adjoin-term (make-term (order t1) (add (coeff t1) (coeff t2))) (+terms (rest-terms l1) (rest-terms l2))))))))))
notice that in this procedure we use the generic operation add. With this implementation we have polynomials whose coefficients can be any number that our system supports
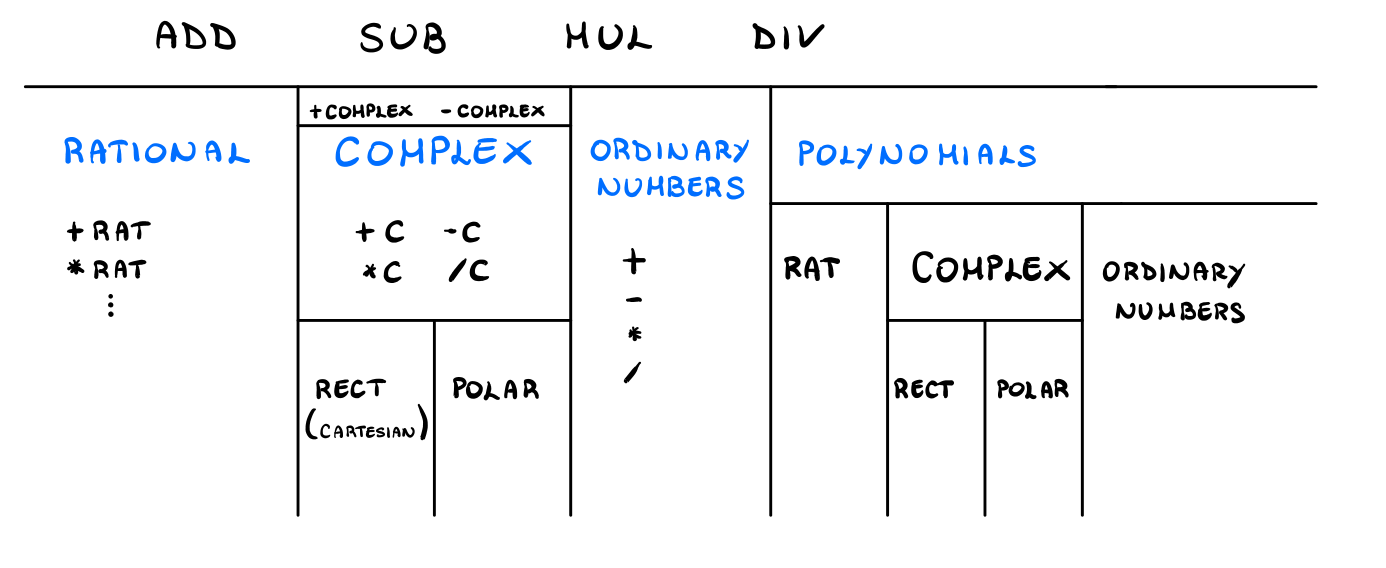
For example we can automatically handle polynomials such as
\[\begin{split} \frac23 \cdot x^2 + \frac{5}{17} \cdot x + \frac{11}{4} \\ (3 + 2i) \cdot x^5 + (4 + 7i) \\ \end{split}\]
We can also add any polynomials we want. Consider for example this polyomial in \(y\), whose coefficients are polynomials in \(x\).
\[(x^2 + 1)y^2 + (x^3 - 2x)y + (x^4 - 7)\]
As we can see, we get a recursive structure
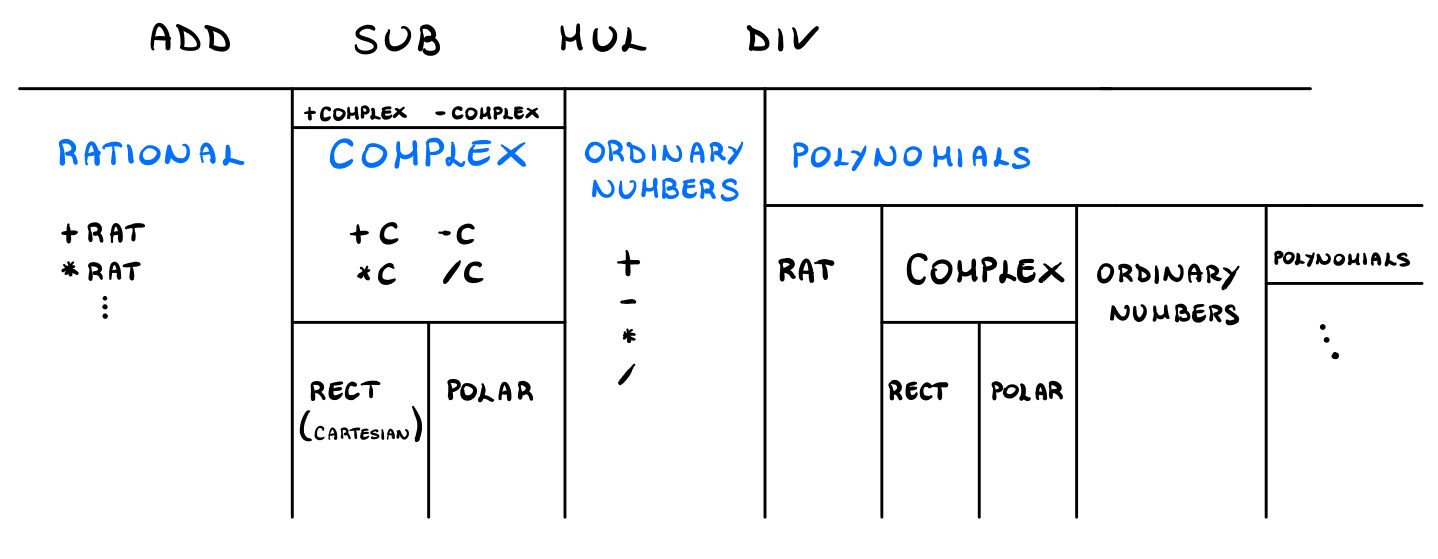
Another way to think about this is that polynomials are a constructors for types: you give them a type, like integers, and it returns to you polynomials in \(x\) whose coefficients are integers, and the important thing about this is that the operations on polynomials reduce to the operations on coefficients.
Consider for example the notion of a generic rational object, such as
\[(3x + 1)/(x^2 + 1)\]
to represent such object we simply have to change, in the definition of our rational number, the symbols +,*,-,/ with add, mult, sub, div.
(define (+rat x y) (make-rat (add (mul (number x) (denom y)) (mul (denom x) (number y))) (mul (denom x) (denom y))))
We can also extend this to matrices.
Notice that the system we built has decentralized control, meaning that there is no single manager which handles the dispatching of the calls, but each party can add themselves to the table.
Notice that our system breaks down when we try to operate on different types of datum such as \(1 + \frac{2}{3}\).