ASD 01 - Problemi, Algoritmi e Modelli di Calcolo
Data:
Table of contents:
Il seguente schema può essere un buon punto per cominciare la nostra trattazione degli algoritmi
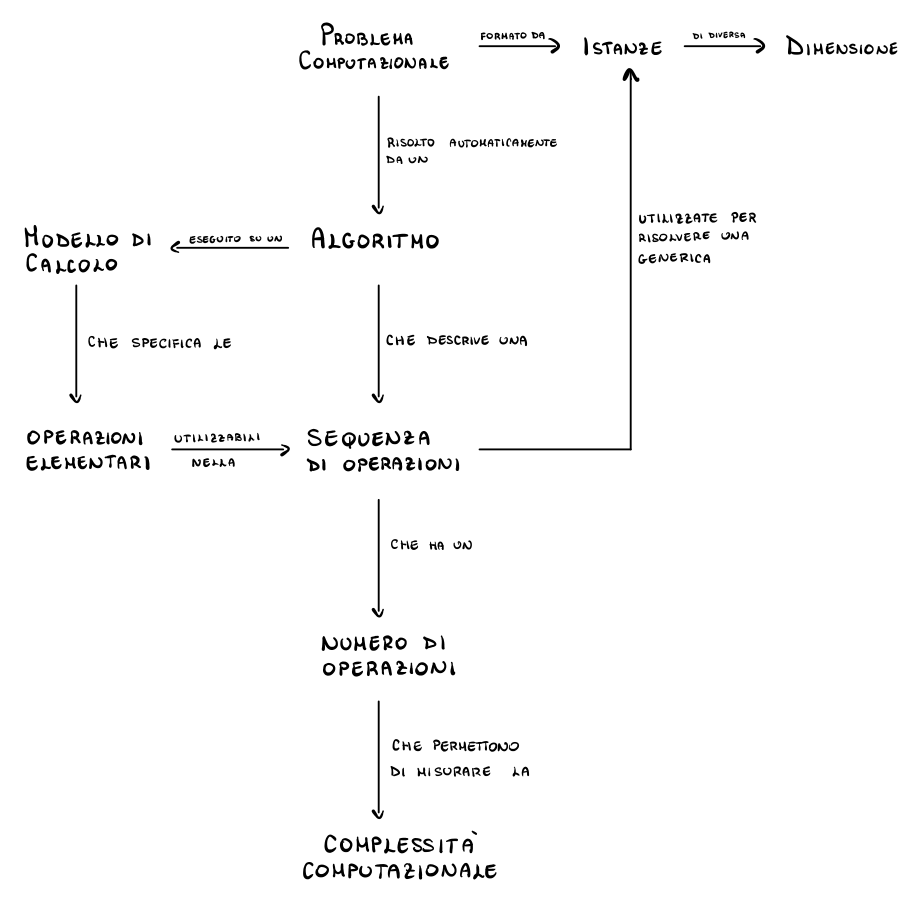
Notiamo in particolare i seguenti concetti fondamentali
Problema Computazionale
Algoritmo
Modello di Calcolo
Complessità computazionale
In questa lezione in particolare saranno discussi informalmente i primi tre concetti, mentre quello della complessità verrà presentato in un successivo video.
Un problema computazionale è un problema che potenzialmente può essere risolto tramite una computazione, ovvero tramite un processo automatico che non necessita alcun tipo di creatività o di intuizione umana. I processi automatici che ci portano alla risoluzione di problemi computazionali prendono molto spesso il nome di algoritmi.
Molti problemi nella nostra vita non ricadono in questa classe di problemi, nel senso che difficilmente riescono ad essere risolti tramite un processo automatico. Prendiamo ad esempio la scrittura creativa. Scrivere un romanzo pone sicuramente una serie di problemi, ma la maggior parte di essi tipicamente non sono problemi di natura computazionale, in quanto hanno a che fare con la nostra creatività e con la nostra abilità di creare delle storie interessanti.
Osservazione: Con l'avvento del machine learning e delle reti neturali, che sono tecniche di apprendimento automatico, questa separazione tra problemi computazionali e problemi non-computazionali sta diventando sempre più sottile, e si ha la sensazione che, potenzialmente, con abbastanza dati, moltissimi problemi potrebbero essere risolti tramite una computazione. Detto questo, i problemi che affronteremo noi saranno problemi "classicamente computazionali".
Andiamo quindi a vedere qualche esempio di problema computazionale.
Il problema dell'ordinamento (sorting, in inglese), è un problema molto intuitivo: data una sequenza di numeri, vogliamo ordinare questa sequenza per ritornare la sequenza ordinata. Le istanze di questo problema in particolare sono sequenze di numeri, e la dimensione di una istanza è il numero di elementi da ordinare.
Per fare qualche esempio, consideriamo il seguente mapping tra input (sequenze a sinistra) e output (sequenze a destra), e le relative dimension.
\[\begin{split} &[2, 3, 1, 0] &\longrightarrow &[0, 1, 2, 3] \,\,\,&,\,\,\, \text{dim} = 4\\ &[10, 0, 2] &\longrightarrow &[0, 2, 10] \,\,\,&,\,\,\, \text{dim} = 3\\ &[5, -5, 1] &\longrightarrow &[-5, 1, 5] \,\,\,&,\,\,\, \text{dim} = 3\\ \end{split}\]
Per questo problema l'istanza generale è una generica sequenza di interi \([a_1, a_2, \ldots, a_n]\) con \(a_i \in \mathbb{R}\). Il problema dell'ordinamento consiste quindi nel prendere questa sequenza generale ed ordinarla
\[[a_1, a_2, \ldots, a_n] \longrightarrow [a_{i_1}, a_{i_2}, \ldots, a_{i_n}]\]
con \(a_{i_1} \leq a_{i_2} \leq \ldots \leq a_{i_n}\). La dimensione di questa istanza generale è pari a \(n\).
Un altro problema computazionale molto famoso nell'algoritmica è il problema del cammino minimo. Questo problema è definito su una struttura dati fondamentale chiamata grafo. Un grafo può essere rappresentato graficamente come un insieme di nodi (punti, o vertici), e un insieme di archi (freccie, segmenti) che collegano coppie di nodi. A ciascun arco poi possiamo associare un valore numerico, che possiamo pensare intuitivamente come la "lunghezza" dell'arco. In quest'ultimo caso abbiamo quello che viene chiamato grafo pesato.
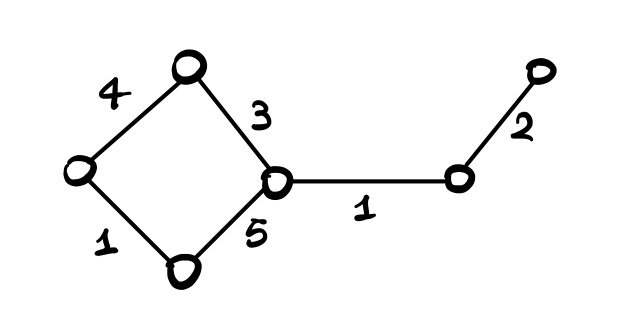
Formalmente tale struttura è rappresentata dalla tripla \(G = (V, E, w)\).
Il problema del cammino minimo prende in input un grafo \(G\) e una coppia di nodi \(s, t\) in \(G\) e consiste nel trovare un cammino \(\pi_{s, t}\) che collega \(s\) a \(t\) minimizzando il peso totale \(\sum_{e \in \pi_{s, t}} w_e\).
Consideriamo, ad esempio, la seguente istanza:
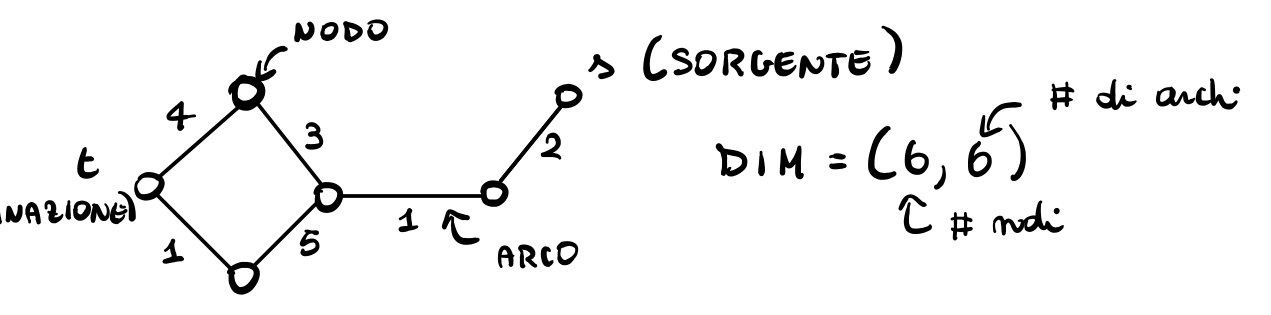
Notiamo che abbiamo due possibili cammini per arrivare da \(s\) a \(t\):
Cammino 1:
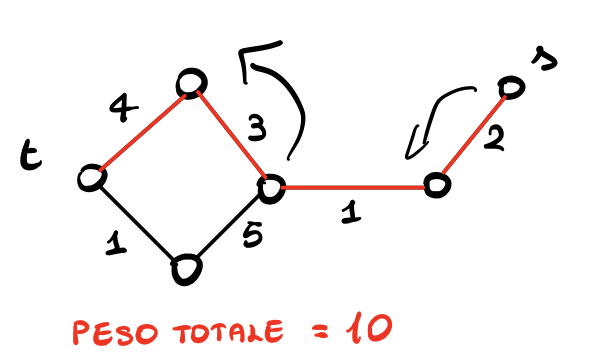
Cammino 2:
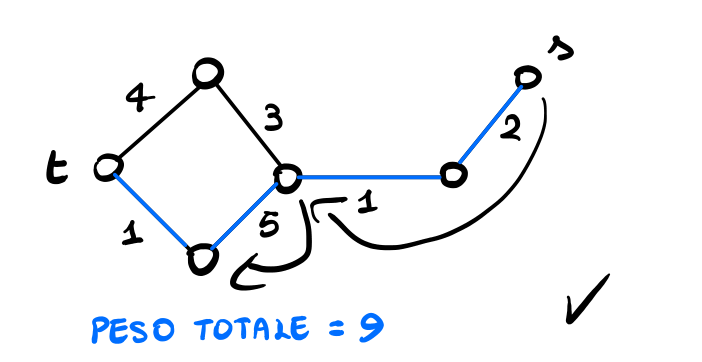
Un altro problema, sempre definito su un grafo \(G = (V, E, w)\), consiste nel trovare un albero ricoprente \(T = (V, E')\), \(E' \subseteq E\) che minimizza il peso totale \(\sum_{e \in T} w_e\).
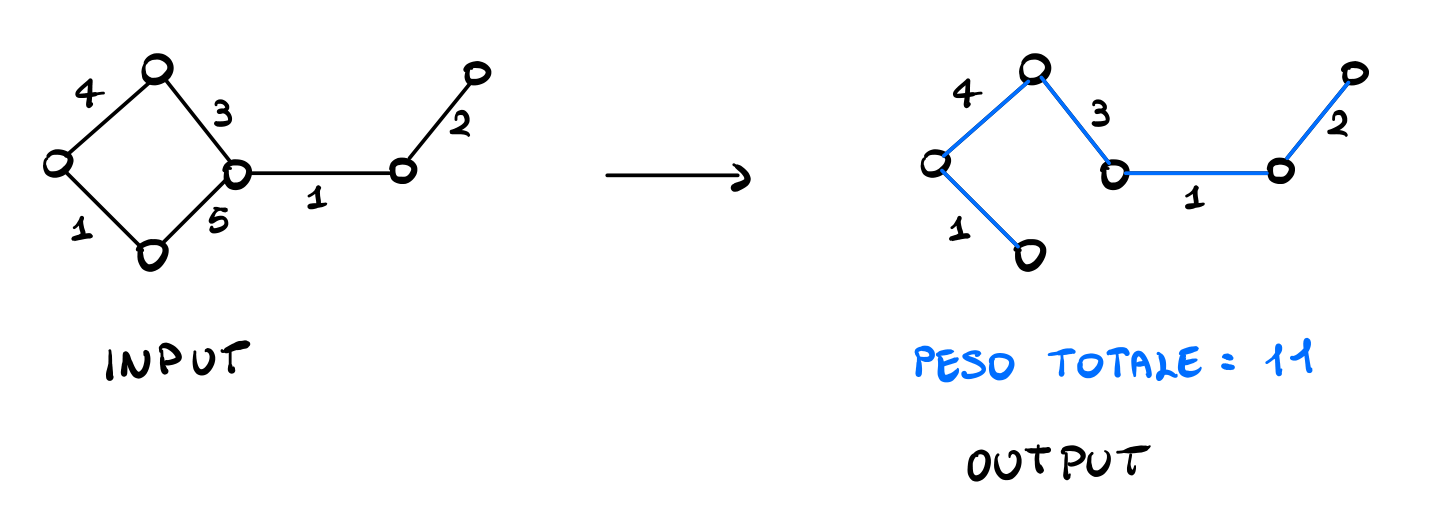
Un algoritmo è una sequenza di operazioni elementari che permettono di risolvere una generica istanza di un problema computazionale
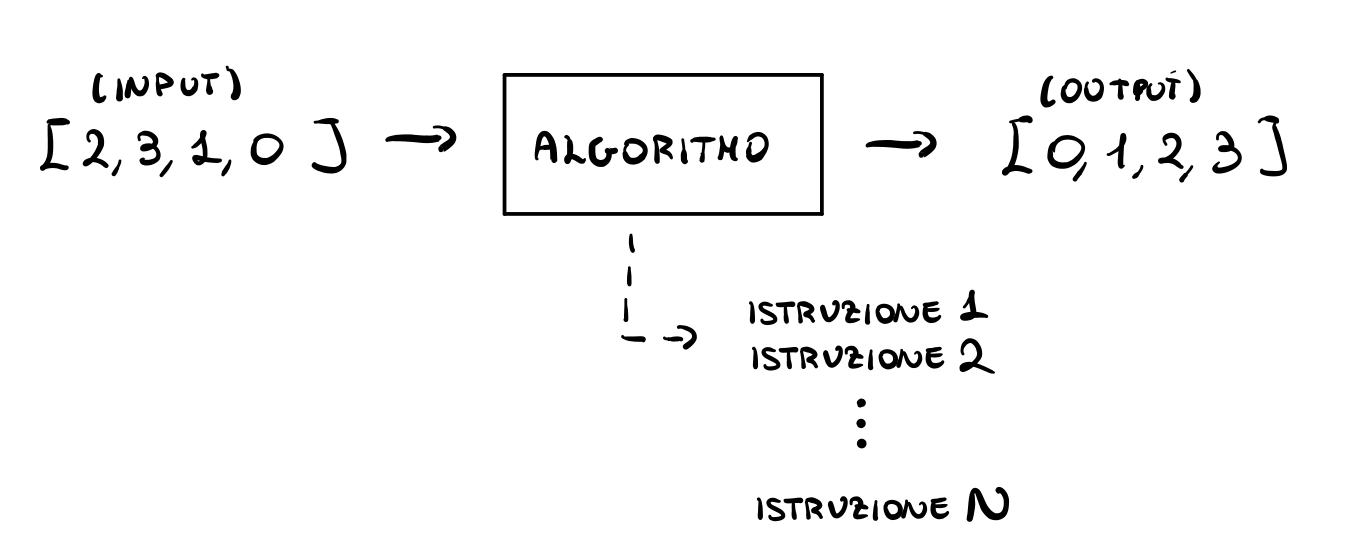
Il modello di calcolo specifica quali sono le possibili operazioni elementari che un algoritmo eseguito su quel modello di calcolo può utilizzare.
Intuitivamente possiamo effettuare la seguente associazione:
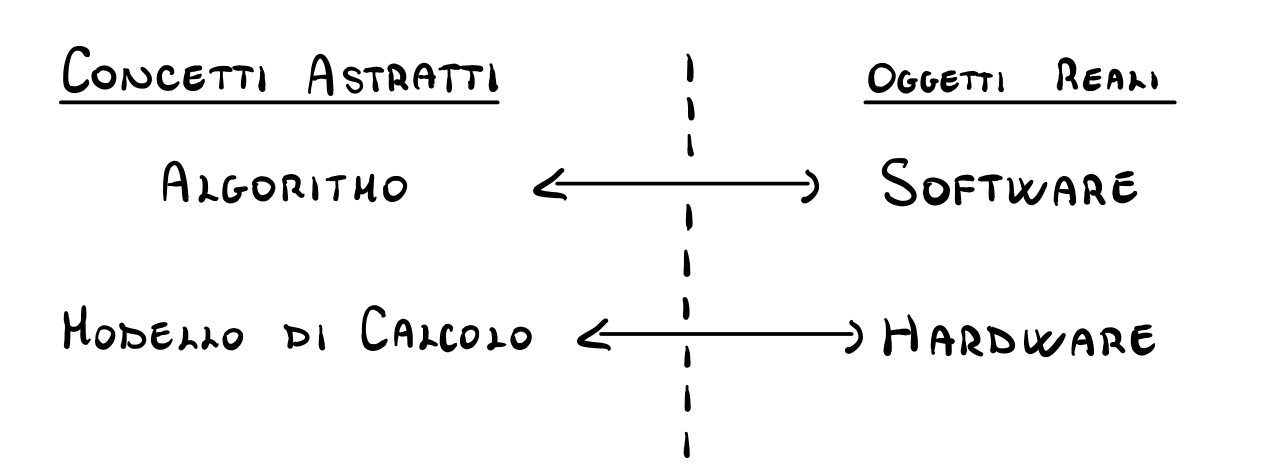
Uno dei primi modelli di calcolo fu introdotto da Alan Turing (1912, 1954) ed è oggi noto sotto il nome di macchina di Turing.
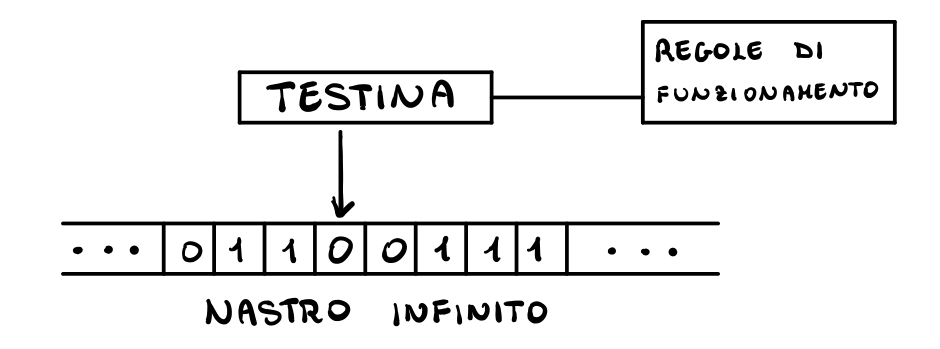
Anche se la macchina di turing è stato uno strumento molto importante per studiare in modo formale il concetto di computazione, questo modello di calcolo è estremamente semplice e primitivo, ed è quindi non adatto per analizzare i problemi da noi considerati. Per risolvere uesto problema si introduce quindi il modello RAM, che sta per Random Access Machine.
La random access machine è basata sulla famosa architettura introdotta da John von Neumann (1903, 1957).
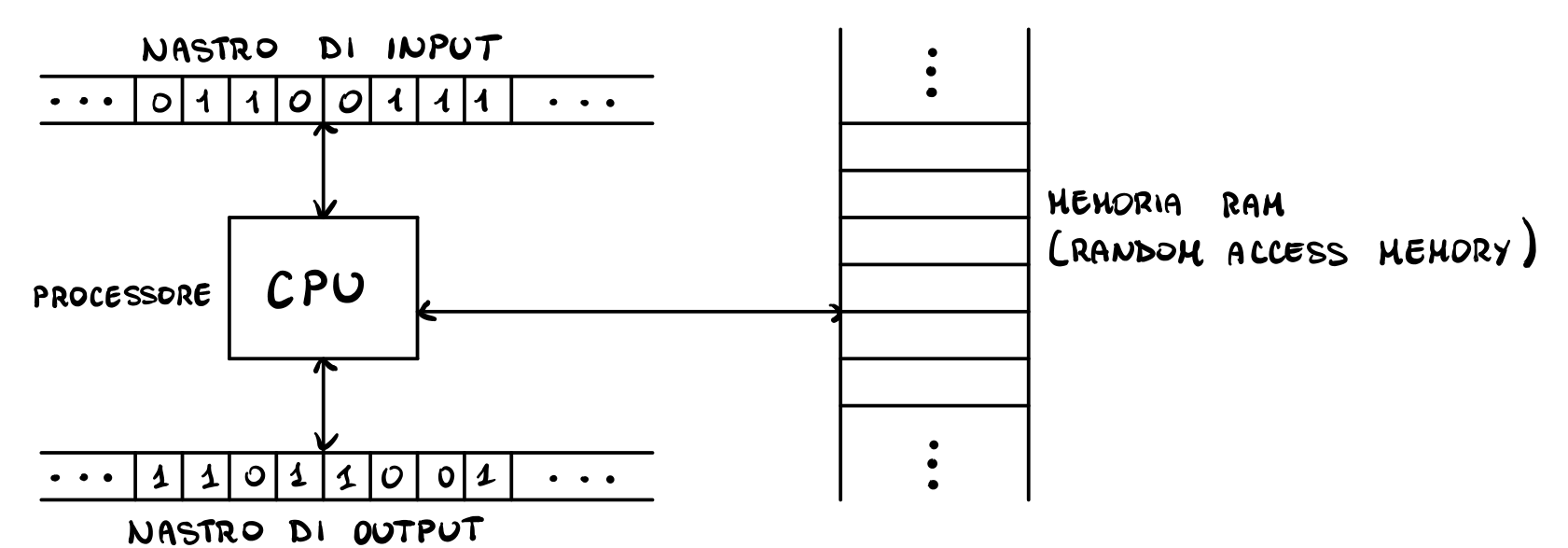
Anche se il modello RAM presenta un livello di astrazione più elevato del modello macchina di turing, questi due modelli sono equivalenti, ovvero tutto ciò che può essere calcolato su un modello può anche essere calcolato sull'altro modello.
Consideriamo adesso un problema particolare, in modo da vedere come tutti questi concetti astratti vengono effettivamente utilizzati.
Dati due interi \(a, b \in \mathbb{N} = \{0, 1, 2, 3, \ldots\}\) sappiamo che possiamo dividere \(a\) per \(b\) per ottenere altri due interi \(q, r\) tali che
\[a = q \cdot b + r \,\,\,\,,\,\,\,\, 0 \leq r < b\]
dove \(q\) è detto quoziente e \(r\) è detto resto. Nel caso in cui \(r = 0\), allora possiamo dire che "\(b\) divide \(a\)".
Per fare qualche esempio:
\(2\) divide \(4\), infatti \(4 = 2 \cdot 2 + 0\)
\(3\) divide \(6\), infatti \(6 = 2 \cdot 3 + 0\)
\(2\) non divide \(7\), infatti \(7 = 2 \cdot 3 + 1\)
Introduciamo quindi la seguente definizione.
Def: Dato un numero naturale \(n\), diciamo che \(n\) è primo se i suoi unici divisori sono \(1\) e \(n\).
Ad esempio,
\(10\) è primo? No, infatti \(5\) divide \(10\).
\(7\) è primo? Si, infatti tra \(2, 3, 4, 5, 6\) nessun numero divide \(7\).
Il problema della primalità è quindi così definito: dato un intero \(n \in \mathbb{B} = \{0, 1, 2, \ldots\}\), dobbiamo stabilire se \(n\) è primo.
Per verificare se \(n\) è primo possiamo utilizzare il seguente algoritmo: scorriamo tutti i numeri tra \(2\) e \(n-1\), dividendo ciascun numero con \(n\). Appena troviamo un numero che divide \(n\) senza resto, ritorniamo false per indicare che il numero \(n\) non è primo. Se, dopo aver controllato tutti i numeri tra \(2\) e \(n-1\), nessuno di questi divide \(n\), allora ritorniamo true, indicando con ciò che \(n\) è primo.
L'idea descritta può essere descritta tramite il seguente pseudo-codice
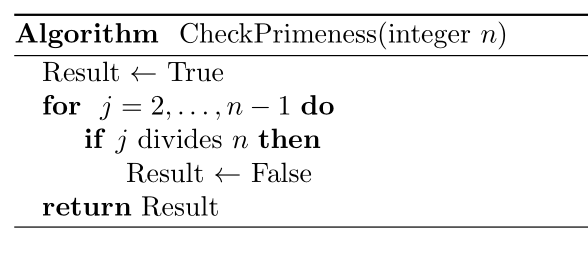
Infine, riportiamo il codice python che implementa lo stesso pseudo-codice
def check_primeness(n): result = True for j in range(2, n): if n % j == 0: result = False return result
Tale codice può poi essere utilizzato in vari modi. A seguire ne mostriamo un possibile utilizzo: generare la lista dei numeri primi tra un certo intervallo
list_of_numbers = list(range(2, 10000)) list_of_prime_numbers = [] for elem in list_of_numbers: if check_primeness(elem) is True: list_of_prime_numbers.append(elem) print(len(list_of_prime_numbers))