Bleichenbacher's Oracle
Leonardo Tamiano
Overview
I'm Leonardo Tamiano, and currently I'm studying a bunch of cryptographic attacks for my master's thesis.
\[\require{color}\]
In this video I will try to explain a famous cryptographic attack which can be done to old vulnerable SSL and TLS servers that still support RSA with padding scheme PKCS #1 v1.5 as the key exchange method.
The attack is called Bleichenbacher's Oracle, and it was discovered by Daniel Bleichenbacher in '98.

The mathematics of the paper can be a bit hard to read, especially for those who struggle with mathematical formalism.
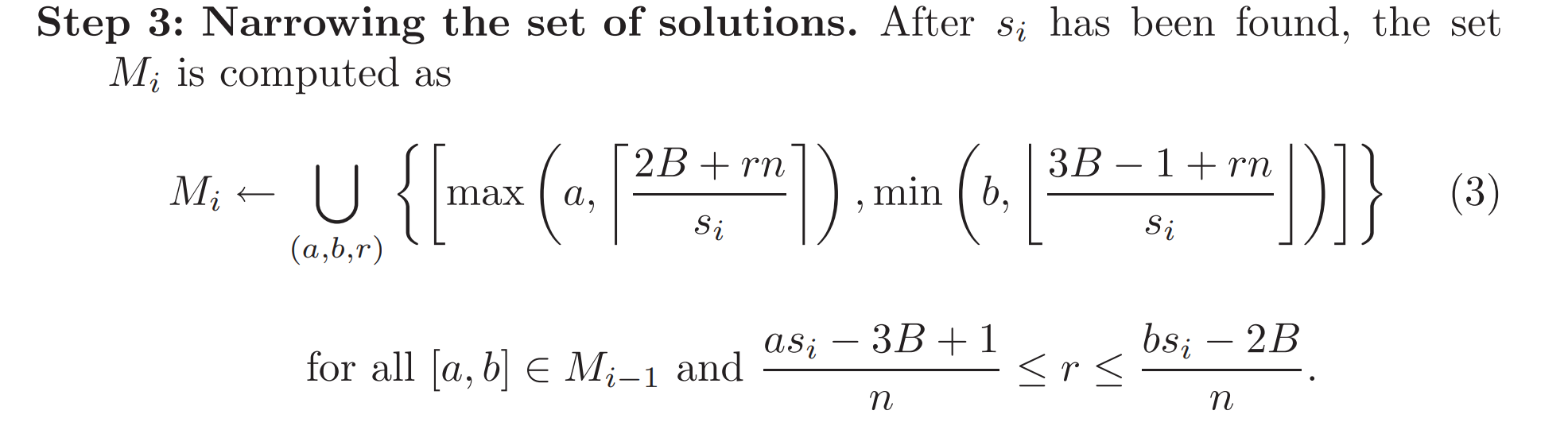
Anyhow, the computational idea behind the attack is simple and beautiful, and the attack itself can be implemented in a few lines of code.
s = ceil(N, B3)
M = set([ (B2, B3 - 1) ])
while True:
if len(M) > 1 or TOTAL_REQUESTS == 0:
s = bleichenbacher_step_1(s)
else:
interval = M.pop()
if interval[0] == interval[1]:
print(f"Found result: {interval[0]}")
break
else:
M.add(interval)
s = bleichenbacher_opt_1(s, M)
M = bleichenbacher_step_2(s, M)
Let's try to understand something…
TLS Handshake
The TLS protocol suite is used to create a secure communication channel on top of a typical TCP socket between a client and a server.
The creation of the cryptographic session which takes care of the security is delegated to the
TLS handshake phase
In this phase client and server send each-others messages in order to:
- Decide on what kind of crypto to use.
- Transfer the session secret (pre-master-key).
In order to transfer the session secret the protocol relies on public key cryptography schemes.
There are different types of public key crypto, such as:
- Diffie-Hellman (on finite groups).
- Diffie-Hellman (on elliptic curves).
- RSA.
The bleichenbacher's attack can be applied only when RSA is used along with a specific padding scheme known as PKCS #1 v1.5.
TLS < 1.3 Handshake (RSA Transport)
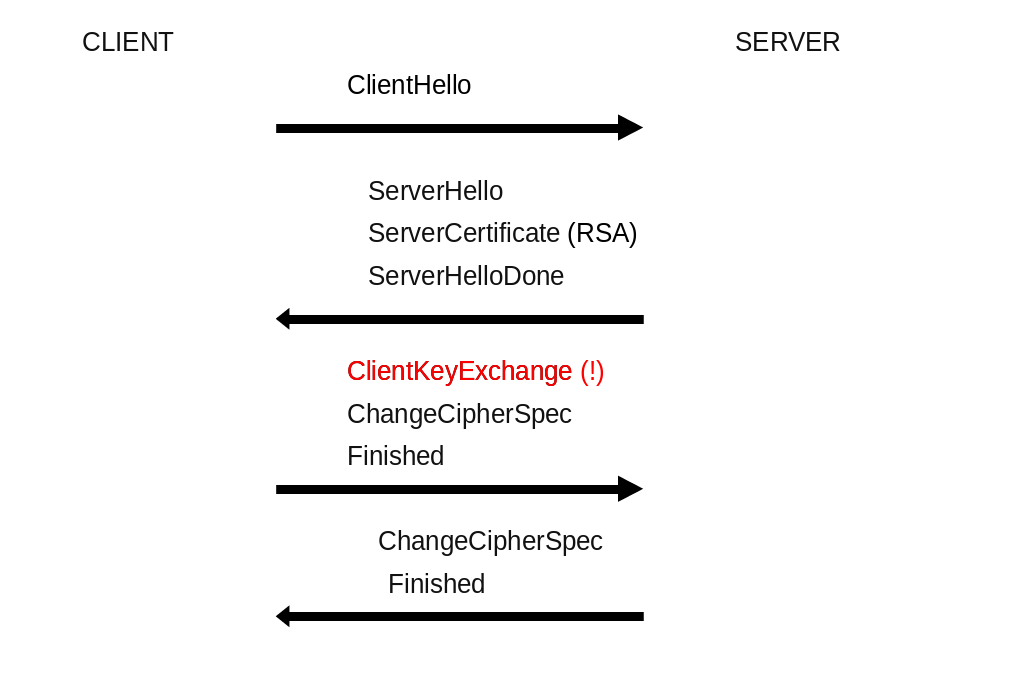
As an attacker, the message we're interested in is the ClientKeyExchange.
This message contains the pre-master-key which is encrypted with the public RSA key of the server the client is connecting to.
By decrypting this message we get access to the entire session.
Textbook RSA
RSA is a public cryptography system which can be used, among other things, for:
- Encryption of messages, granting confidentiality.
- Signing of messages, granting authenticity.
To give these properties RSA makes use of certain results taken from classical number theory.
When working with RSA, the following holds:
- Messages are seen as simple numbers.
- All work is done in a modular arithmetic.
- Encryption and decryption are implemented through modular exponentiation.
Process of generating a public/private key in RSA
- We choose \(p\) and \(q\), two big primes distant from eachothers.
We compute \(N\) and \(\Phi(N)\) as
\[N = p \cdot q\] \[\Phi(N) = (p-1) \cdot (q - 1)\]
- We choose \(e < \Phi(N)\) coprime with \(\Phi(N)\).
We compute \(d\) by solving
\[d \equiv e^{-1} \mod \Phi(N)\]
To encrypt a message \(m \in [0, N)\) we use modular exponentiation
\[c = m^e \mod N\]
NOTE: Everyone can encrypt messages, as \((e, N)\) is the public key.
To decrypt an encrypted message \(c \in [0, N)\) we proceed once again with modular exponentiation
\[m = c^d \mod N\]
NOTE: Only the owner of the private key \(d\) can decrypt messages.
The correctness of RSA relies on the famous Euler's Theorem, which states that
\[a \equiv 1 \mod \Phi(N) \implies m^{a} \equiv m \mod N\]
In particular, given that
- \[e \equiv d^{-1} \mod \Phi(N) \implies e \cdot d \equiv 1 \mod \Phi(N)\]
- \[c^d \mod N \equiv (m^e)^d \mod N \equiv m^{e \cdot d} \mod N\]
we have
\[c^d \mod N \equiv m^{e \cdot d} \mod N \equiv m \mod N\]
The security of RSA on the other hand is based on the computational intractability of the factorization problem.
By knowing only \((N, e)\), we're not able to compute \(d\), because for computing \(d\) we have to solve the congruence
\[d \equiv e^{-1} \mod \Phi(N)\]
that is, we have to compute the inverse of \(e\) in \(\mathbb{Z}_{\Phi(N)}\).
This can be done in a fast way only by knowing
\[\Phi(N) = (P - 1) \cdot (Q - 1)\]
which requires being able to factorize \(N\) into its prime factors.
Malleability
The RSA cryptosystem is said to be malleable.
Given an encrypted text and a public key
\[c = m^e \mod N, \;\;\;\; (e, N)\]
we can compute a new value
\[s^e \cdot c \mod N\]
and this new value can be seen as a new ciphertext
\[\begin{split} s^e \cdot c \mod N &= s^e \cdot m^e \mod N \\ &= (s \cdot m)^e \mod N \\ \end{split}\]
in particular we can know the exact relationship between the plaintext of our new crafted ciphertext and the plaintext of the original ciphertext.
| Plaintext | Ciphertext |
|---|---|
| \(m\) | \(c = m^e \mod N\) |
| \(s \cdot m \mod N\) | \(s^e \cdot c \mod N\) |
Why textbooks better remain on the shelves
The crypto system we just described is known as textbook RSA.
This name comes from the fact that this system is only secure in the pages of a book.
In the real and scary world a system like this presents various problems…
For example, given that the system is completely deterministic, if we send two times the same message \(m\), the resulting ciphertext will be the same as well.
- \(m \longrightarrow c = m^e \mod N \;\;\;\;\;, \;\;\;\; \text{ time } t_1\)
- \(m \longrightarrow c = m^e \mod N \;\;\;\;\;, \;\;\;\; \text{ time } t_2 > t_1\)
This means we lose semantic security.
To solve this problem, in 1993 a padding scheme known as PKCS #1 v1.5 was standardized.
It's possible to generate RSA keys with the ssh-keygen command
ssh-keygen -t rsa -b 1024 -N "" -f rsa_key
PKCS #1 v1.5
Consider we want to transmit a message.
The idea is to start from the message bytes and construct a particular number
\[m \in [0, N)\]
The number will be generated using randomness.
To this end let's assume that the byte-length of \(N\) is \(k\).
\[\begin{split} \text{Message bytes} &\longrightarrow \text{Padding bytes + Message bytes} \\ &\longrightarrow m \in [0, N) \end{split}\]
Padding scheme PKCS #1 v1.5 (1/5)
\[\text{0x 00 02} \;\; | \;\; RB_1 \; \ldots \; RB_i \;\; | \;\; \text{00} \;\; | \;\; MB_1 \; \ldots \; MB_j\]
Padding scheme PKCS #1 v1.5 (2/5)
- First two bytes are set to
0x00and0x02. - At least
8random bytes different from0x00. - A single null byte
0x00. - The remaining bytes are the message's byte.
Padding scheme PKCS #1 v1.5 (3/5)
\[\text{0x 00 02} \;\; | \;\; \underbrace{RB_1 \; \ldots \; RB_i}_{\geq 8} \;\; | \;\; \text{00} \;\; | \;\; MB_1 \; \ldots \; MB_j\]
Padding scheme PKCS #1 v1.5 (4/5)
From the second constraint (2) it follows that
we can have at most \(k - 11\) application data bytes per packet
In case our message is longer than that, the idea is to split the message in multiple packets.
Padding scheme PKCS #1 v1.5 (5/5)
\[\overbrace{\text{0x 00 02} \;\; | \;\; \underbrace{RB_1 \; \ldots \; RB_i}_{\geq 8} \;\; | \;\; \text{00} \;\; | \;\; \underbrace{MB_1 \; \ldots \; MB_j}_{\leq k - 11}}^k\]
if __name__ == "__main__":
if len(sys.argv) != 3:
print(f"Usage: {sys.argv[0]} <msg> <key_size (in bits)>")
exit()
else:
msg = sys.argv[1]
msg_length = len(msg)
key_size = int(int(sys.argv[2]) / 8) # transform size in bytes
if msg_length > key_size - 11:
print(f"[PKCS#1 v1.5 error] message length ({msg_length}) is too long for given key size ({key_size})")
exit()
padding_length = key_size - len(msg) - 3
padding = "\x01" * padding_length # NOTE: this should be randomic
padded_msg = "\x00" + "\x02" + padding + "\x00" + msg
print(padded_msg, end='')
00000000 00 02 01 01 01 01 01 01 01 01 01 01 01 01 01 01 |................| 00000010 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 01 |................| ... 00000070 01 01 01 01 00 68 65 6c 6c 6f 20 77 6f 72 6c 64 |.....hello world| 00000080
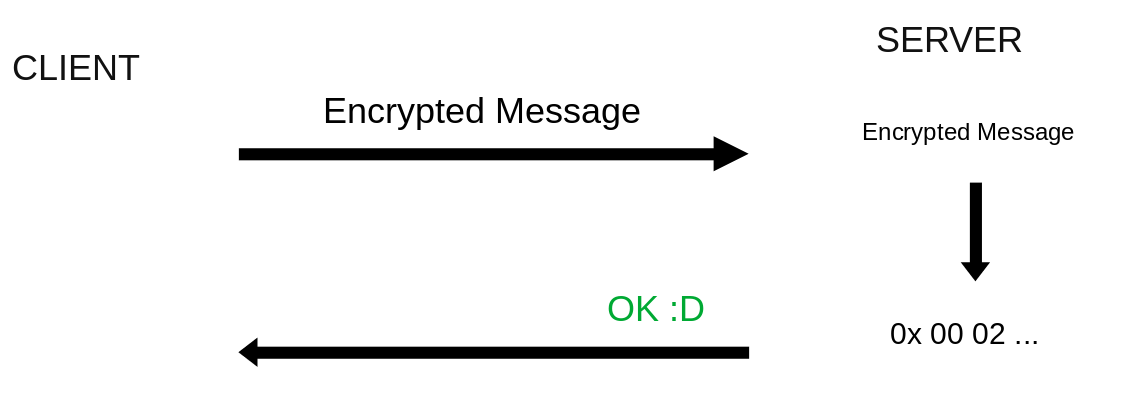
Oracles on TLS (RSA + PKCS #1 v1.5)
Let's assume now that we can interact with a TLS server in a way
that when we send the message padded with PKCS #1 v1.5 and encrypted
with RSA the server let us distinguish the following two
situations:
The encrypted message, once decrypted, is correctly padded according
to PKCS #1 v1.5.
The encrypted message, once decrypted, is NOT correctly padded according
to PKCS #1 v1.5.
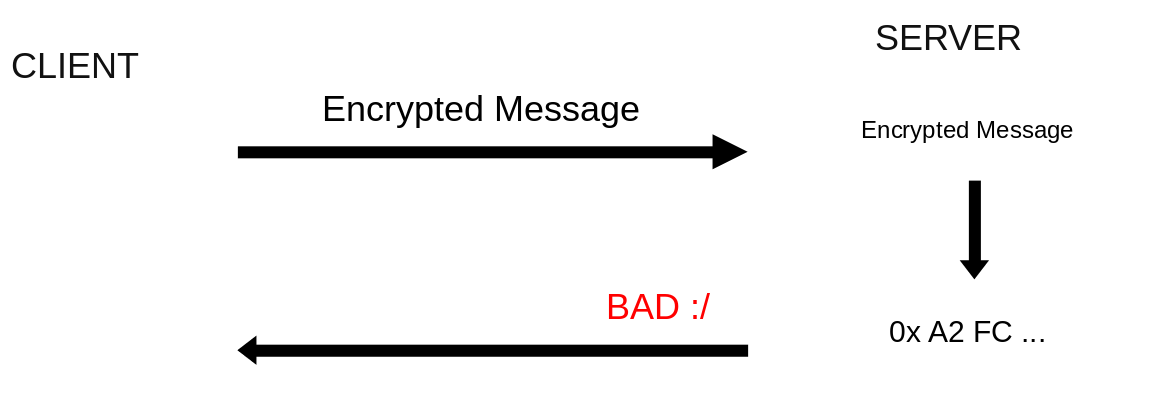
In these cases it is said that the server offers a cryptographic oracle.
We can have various oracles, depending on what kind of things are checked with respect to the plaintext message's bytes.
The more checks are made, and the harder it is to produce messages that satisfy all constraints.
In this presentation we assume to have a single oracle that only checks the first two bytes of the message
def oracle(msg_hex):
global D, N
# transform hex into number
encrypted_msg = int("0x" + msg_hex, 0)
# raw decrypt using RSA
decrypted_msg = pow(encrypted_msg, D, N)
decrypted_hex = f"%0{PADDING_VALUE}x" % decrypted_msg
# check for padding
if decrypted_hex[0:4] != "0002":
return False
else:
return True
Bleichenbacher's Attack
The bleichenbacher attack is an
adaptive choosen ciphertext attack
which uses a cryptographic oracle based on RSA and PKCS #1 v1.5 to
decrypt any message \(c\) which was encrypted using the public key of
the TLS server we're trying to attack.
The attack is based on the following things:
- In RSA both plaintext and ciphertext are numbers.
- Satisfying all padding rules of
PKCS #1 v1.5puts heavy contraints on the numerical range the plaintext can belong to. - The malleability of RSA allows an attacker to create new ciphertexts whos plaintexts can be related to the original plaintext.
Let \(m\) be a message padded with PKCS #1 v1.5, and let \(c\) be its encrypted form.
By using \(c\) and the crypto oracle our objective is to find the original \(m\).
NOTE: The attack can still be done if \(m\) is any message (even not correctly padded), but it requires an additional starting phase which we'll briefly cover at the end.
Consequences of PKCS #1 v1.5
If we remember how the padding standard PKCS #1 v1.5 was defined,
we'll recall that all messages that satisfy this padding scheme
start with the byte sequence 0x 00 02.
Let \(k\) be the size in byte of the modulus \(N\), where \(N\) is part of the public key of the server.
By defining
\[B = 2^{8 \cdot(k - 2)}\]
we have that
\[\begin{split} B &\longrightarrow \text{0x 00 01 } \overbrace{\text{00 00} \ldots \text{00}}^{k - 2 \text{ bytes}}\\ 2B &\longrightarrow \text{0x 00 02 } \text{ 00 00} \ldots \text{00} \\ 3B &\longrightarrow \text{0x 00 03 } \text{ 00 00} \ldots \text{00} \\ \end{split}\]
This means that,
\[2B \leq m \leq 3B - 1\]
Decryption Algorithm In \(\epsilon\) Minutes
The decryption algorithm works in various phases.
Each phase is indexed by a natural number \(i \in \mathbb{N}\) and contains two different steps.
The step for each phase are described as follows:
The first step tries to find a value \(s_i\) such that
\[s_i \cdot m \mod N\;\;\; \text{ is PKCS #1 v1.5 compliant}\]
The second step constructs, starting from the \(s_i\) discovered previously, a set of intervals \(M_i\) such that
\[\exists [a, b] \in M_i: \;\; m \in [a, b]\]
Initialization phase: \(i = 0\)
At the start we initialize the following values
\[\begin{split} s_0 &= 2 \\ & \\ M_0 &= \{\;\; [2B, 3B - 1] \;\;\} \\ \end{split}\]
Generic phase: \(i \in \mathbb{N}^+\)
Step 1: Search for next \(s_i\)
Step 1: Search for next \(s_i\)
We start from \(s_i = s_{i-1} + 1\) and find the next value such that
\[s_i \cdot m \mod N\;\;\; \text{ is PKCS #1 v1.5 compliant}\]
if a given \(s_i\) does not work, we try the next \(s_i = s_i + 1\)
Step 1: Search for next \(s_i\)
To test a given \(s_i\) we send to the oracle the following value
\[s_i^e \cdot c \mod N\]
If the oracle replies with "YES", then we stop and go to the next step, otherwise we keep going and update \(s_i\).
Step 1: Search for next \(s_i\)
The code for this phase is
def bleichenbacher_step_1(s):
global E, N, TOTAL_REQUESTS
s = s + 1
while True:
new_ciphertext = (pow(s, E, N) * ENCRYPTED_FLAG) % N
encrypted_hex = f"%0{PADDING_VALUE}x" % new_ciphertext
if oracle(encrypted_hex) == True:
return s
s = s + 1
TOTAL_REQUESTS += 1
Step 2: Construction of \(M_i\)
Step 2: Construction of \(M_i\)
Suppose we found a value \(s_i\) such that
\[s_i \cdot m \mod N \;\;\; \text{ è PKCS #1 v1.5 compliant}\]
The idea now is to use the value \(s_i\) to propagate the knowledge of \(M_{i-1}\) in the new set \(M_{i}\), and, while doing so, restrict the size of the new intervals so that we can understand better where \(m\) is located.
Step 2: Construction of \(M_i\)
We already saw that
\[s_i \cdot m \mod N \;\;\; \text{ is PKCS #1 v1.5 compliant}\]
implies
\[2B \leq s_i \cdot m \mod N \leq 3B - 1\]
Step 2: Construction of \(M_i\)
For how we define the modulus, we have that
\[2B \leq s_i \cdot m \mod N \leq 3B - 1\]
implies that there exists a \(k \in \mathbb{Z}\) such that
\[2B \leq s_i \cdot m - k \cdot N \leq 3B - 1\]
Step 2: Construction of \(M_i\)
Summarizing,
- \(s^e \cdot c \mod N\) is accepted by the oracle.
- \(s \cdot m \mod N\) is PKCS #1 v1.5 compliant.
- \(2B \leq s \cdot m \mod N \leq 3B - 1\)
- \(\exists k \in \mathbb{Z}: \;\; 2B \leq s \cdot m - k \cdot N \leq 3B - 1\)
Step 2: Construction of \(M_i\)
From
\[2B \leq s_i \cdot m - k \cdot N \leq 3B - 1\]
we get
\[\begin{split} \frac{2B + k \cdot N}{s_i} \leq m \leq \frac{3B - 1 + k \cdot N}{s_i} \end{split}\]
Step 2: Construction of \(M_i\)
PROBLEM: we do not know \(k\)
\[\begin{split} \frac{2B + \textcolor{red}{k} \cdot N}{s_i} \leq m \leq \frac{3B - 1 + \textcolor{red}{k} \cdot N}{s_i} \end{split}\]
Step 2: Construction of \(M_i\)
SOLUTION: having fixed both \(s\) and \(m\), we can enumerate all possible values of \(k\)
\[2B \leq s_i \cdot m - k \cdot N \leq 3B - 1\]
\(\implies\)
\[\frac{-3B + 1 + s_i \cdot m}{N} \leq k \leq \frac{-2B + s_i \cdot m}{N}\]
Step 2: Construction of \(M_i\)
For example, from the bound \(m \in [2B, 3B - 1]\) we have that
\[\]
\[\frac{-3B + 1 + s_i \cdot \textcolor{red}{2B} }{N} \leq \frac{-3B + 1 + s_i \cdot \textcolor{red}{m}}{N} \leq k\]
\[\]
\[k \leq \frac{-2B + s_i \cdot \textcolor{blue}{m}}{N} \leq \frac{-2B + s_i \cdot (\textcolor{blue}{3B - 1})}{N}\]
Step 2: Construction of \(M_i\)
Thus, for each value of \(k\) taken from the interval
\[\frac{-3B + 1 + s_i \cdot 2B}{N} \leq k \leq \frac{-2B + s_i \cdot (3B - 1)}{N}\]
we have a new possible interval for \(m\)
\[\frac{2B + k \cdot N}{s_i} \leq m \leq \frac{3B - 1 + k \cdot N}{s_i}\]
Step 2: Construction of \(M_i\)
Out of all this intervals, \(m\) belongs to only one of them, associated to a specific value of \(k\).
Given however that we don't know the particular \(k\), we proceed by saving all of valid the intervals in the new set \(M_i\).
Step 2: Construction of \(M_i\)
More specifically, given \([a, b] \in M_{i-1}\), we obtain the following range for \(k\)
\[\frac{-3B + 1 + s_i \cdot \textcolor{red}{a}}{N} \leq k \leq \frac{-2B + s_i \cdot \textcolor{blue}{b}}{N}\]
and for every value in this range we get a new possible interval for \(m\)
\[\frac{2B + k \cdot N}{s_i} \leq m \leq \frac{3B -1 + k \cdot N}{s_i}\]
Step 2: Construction of \(M_i\)
A particular interval is added to \(M_i\) only if it has a non-empty intersection with \([a, b] \in M_{i-1}\).
To compute these intersection the max and min functions are used.
Step 2: Construction of \(M_i\)
Graphically, for every \([a, b] \in M_{i-1}\) and for every \(k\) in the relative range we can have four possible valid cases with respect to the intersection of the new interval
\[[aa, bb] = \Bigg[\frac{2B + k \cdot N}{s_i}, \;\; \frac{3B -1 + k \cdot N}{s_i}\Bigg]\]
to the old one \([a, b]\).
Step 2: Construction of \(M_i\)
Case 1/4
\[\begin{cases} \max(a, aa) &= a \\ \min(b, bb) &= b \\ \end{cases}\]

Step 2: Construction of \(M_i\)
Case 2/4
\[\begin{cases} \max(a, aa) &= aa \\ \min(b, bb) &= b \\ \end{cases}\]

Step 2: Construction of \(M_i\)
Case 3/4
\[\begin{cases} \max(a, aa) &= a \\ \min(b, bb) &= bb \\ \end{cases}\]
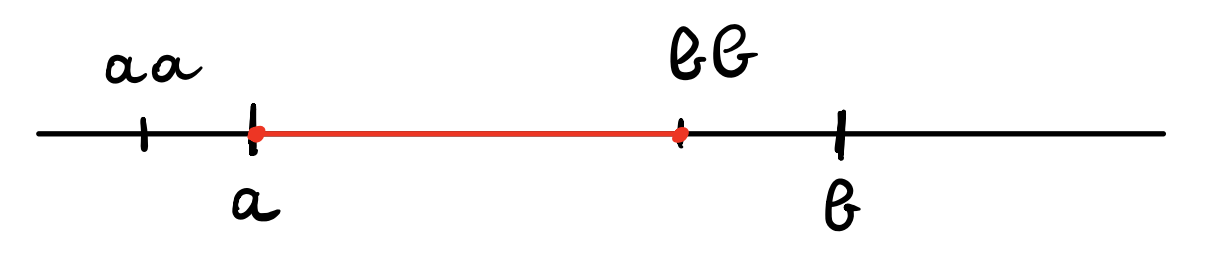
Step 2: Construction of \(M_i\)
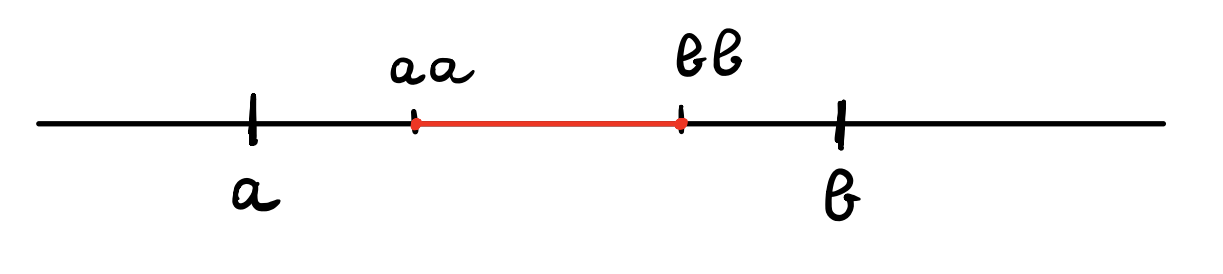
Case 4/4
\[\begin{cases} \max(a, aa) &= aa \\ \min(b, bb) &= bb \\ \end{cases}\]
Step 2: Construction of \(M_i\)
This is the idea behind the following formula
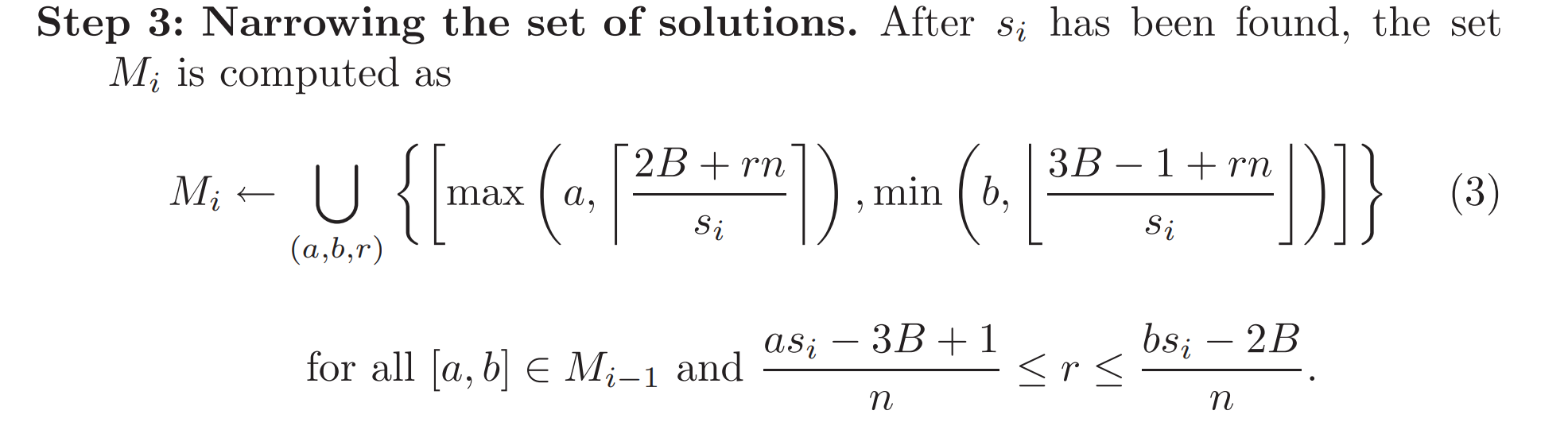
Step 2: Construction of \(M_i\)
Note that at every iteration, the only thing we know for certain about the new set of intervals \(M_i\) is that \(m\) belongs to a single interval of \(M_i\), even though we cannot tell which.
In formula,
\[\exists [a, b] \in M_i: \;\; m \in [a, b]\]
Step 2: Construction of \(M_i\)
The code for this step is
def bleichenbacher_step_2(s, old_M):
new_M = set([])
for (a, b) in old_M:
r1 = ceil((a * s - B3 + 1), N)
r2 = floor((b * s - B2), N) + 1
for r in range(r1, r2):
aa = ceil(B2 + r*N, s)
bb = floor(B3 - 1 + r*N, s)
newa = max(a, aa)
newb = min(b, bb)
if newa <= newb:
new_M |= set([ (newa, newb) ])
return new_M
At the end of this second step for the phase \(i\), if the set \(M_i\) contains a single interval, and if this interval is of the form \([a, a]\), then we can stop, since
\[m \in [a, a] \implies a \leq m \leq a \implies m = a\]
If instead \(M_i\) contains one or more intervals, or if it contains a single interval of the form \([a, b]\), with \(a \neq b\), then the algorithm proceeds towards the next phase \(i + 1\) as described previously.
Original Optimization ('98)
The algorithm just described in theory already works.
In practice however it is just too slow.
The original ('98) paper thus introduces the following two optimizations:
At the start, instead of starting from \(s_0 = 1\), we start with
\[s_0 = \left \lceil \frac{N}{3B} \right \rceil\]
- If at the end of phase \(i\), the set \(M_{i}\) contains a single interval \([a, b]\), then we optimize the search for the next \(s_{i+1}\) by using a heuristic.
The first optimization is a direct consequence of the fact that for value of \(s_0 \leq \left \lceil \frac{N}{3B} \right \rceil\) it is simply not possible to have a PKCS compliant plaintext.
Indeed,
\[k \leq \frac{m_0 \cdot s_1 - 2B}{N} \leq \frac{(3B - 1) \cdot s_1 - 2B}{N} < \frac{3B s_1}{N}\]
Such value is \(1\) when \(s_1 = \frac{N}{3B}\).
If \(s_1 < \frac{N}{3B}\), then \(k < 1 \implies k = 0\).
In these cases
\[m_1 = m_0 \cdot s_1 - k \cdot N = m_0 \cdot s_1 < N\]
and so we can't respect PKCS padding, since the value will never
start with 00 02.
The second optimization instead is based on a heuristic.
The general idea is to have that the next value of \(s_{i+1}\) is, approximately, double the previous value.
In formula,
\[s_{i+1} \approx 2 \cdot s_{i}\]
In detail, if \(M_{i} = \{\;\; [a, b] \;\; \}\), then we let
\[r_i \geq 2 \cdot \frac{b \cdot s_i - 2B}{n}\]
and we start to try all \(s_{i+1}\) in the following interval
\[\frac{2B + r_i \cdot n}{b} \leq s_{i+1} \leq \frac{3B + r_i n}{a}\]
until \(s_{i+1}^e \cdot c \mod N\) is accepted by the oracle.
If the interval
\[\frac{2B + r_i \cdot n}{b} \leq s_{i+1} \leq \frac{3B + r_i n}{a}\]
finishes without finding any valid \(s_{i+1}\), then we increment \(r_i = r_i + 1\) and we start the search for the next \(s_{i+1}\) in the new interval.
Notice that if the value \(s_{i+1}\) works, then we have
\[\begin{split} s_{i+1} &\geq \frac{2B + r_i N}{b} \\ \\ &= \frac{2B +2b s_{i} - 4B}{b} \\ \\ &= 2 s_{i} - \frac{2B}{b} \end{split}\]
So we get,
\[s_{i+1} \approx 2 s_{i} - \frac{2B}{b}\]
and since \(b \geq 2B\), we have that \(2B/b < 1\).
Thus in general \(-2B/b\) is not influent in the final value and we can roughly say that
\[s_{i+1} \approx 2 s_{i-1}\]
The code for this optimization is
def bleichenbacher_opt_1(s, old_M):
global TOTAL_REQUESTS
fst = old_M.pop()
old_M.add(fst)
a = fst[0]
b = fst[1]
r = ceil((b * s - B2) * 2, N)
while True:
low_bound = ceil((B2 + r * N), b)
high_bound = ceil((B3-1 + r * N), a) + 1
for s in range(low_bound, high_bound):
new_ciphertext = (pow(s, E, N) * ENCRYPTED_FLAG) % N
str_hex = f"%0{PADDING_VALUE}x" % new_ciphertext
if oracle(str_hex):
return s
TOTAL_REQUESTS += 1
r += 1
Final code
By putting all the pieces of the puzzle together, we get
s = ceil(N, B3)
M = set([ (B2, B3 - 1) ])
while True:
if len(M) > 1 or TOTAL_REQUESTS == 0:
s = bleichenbacher_step_1(s)
else:
interval = M.pop()
if interval[0] == interval[1]:
print(f"Found result: {interval[0]}")
break
else:
M.add(interval)
s = bleichenbacher_opt_1(s, M)
M = bleichenbacher_step_2(s, M)
Further Optimizations
Throughout the years various other optimizations have been suggested.
All of them try to tackle the following aspects of the algorithm:
- Shorten the search-time for the next \(s_i\).
- Shorten the computation to construct the intervals in \(M_i\).
Some names:
- Tigher Bounds.
- Beta Method.
- Parallel Threads Methods.
- Skipping Holes.
- Trimmers.
The missing step
At the start we assumed that the original plaintext \(m\) was
correctly padded according to PKCS #1 v1.5.
What if that's not the case?
What if we catch a general encrypted message \(c\) and we want to decrypt it, even though the plaintext \(m\) is not PKCS compliant?
The attack can still be done, but before starting we need to find an \(s_0\) value such that
\[c \cdot s_0^e \mod N\]
is accepted by the oracle.
To find that we just generate \(s_0\) randomly and check the oracle.
If its valid, we let \(c = c \cdot s_0^e \mod N\) and start to decrypt \(c\) as we did before.
If its not valid, we generate another \(s_0\) and try again.
References
The following resources were used for the realization of this video.
I express my gratitude towards each and every author.
Thank you (♥)!