La Macchina di Turing
Riassunto
Nella precedente lezione avevamo introdotto le connessioni tra i linguaggi di programmazione e le macchine (modelli di calcolo) in grado di leggere ed eseguire tali linguaggi.
Avevamo poi chiuso il video menzionando il fatto che di modelli di calcolo nel corso degli anni ne sono stati definiti tanti, tra cui:
- Macchine di Turing.
- Funzioni ricorsive.
- Lambda calcolo.
- Le macchine a registri elementari.
- I comuni linguaggi di programmazione.
Eppure, la tesi di Church-Turing menziona solamente le macchine di Turing:
È calcolabile tutto (e solo) ciò che può essere calcolato tramite una macchina di Turing.
In questa lezione andiamo a vedere che cos'è esattamente una macchina di Turing, e perché le macchine di Turing sono un ottimo modello matematico per rappresentare il concetto intuitivo di calcolabilità.
Alan M. Turing
Prima di entrare nei dettagli tecnici, è doveroso fare qualche nota sull'autore di questo modello di calcolo, Alan M. Turing, che oggi è considerato uno dei padri fondatori dell'informatica teorica e dell'intelligenza artificiale.
Alan M. Turing nasce nel 1912 in Inghilterra e muore dopo 42 anni, nel 1954, in seguito ad un morso dato ad una mela intinta col cianuro.
Sono tanti e vari i lavori svolti da Turing nel breve tempo che ha avuto a disposizione. Tra questi spiccano di importanza e rilevanza i seguenti:
- Ha definito il concetto di macchina di Turing. (1936)
- Ha dato notevoli contributi alla decifrazione delle comunicazioni tedesce cifrate con la macchina Enigma. (1939-1945)
- Ha scritto i primi articoli sull'intelligenza artificiale, introducendo il famoso test di Turing (1950).
La vita e le opere di Turing sono troppo complesse per essere riassunte in pochi minuti.
C'è solo una cosa che nella nostra ignoranza possiamo dire riguardo ad una persona come Turing:
Ha dedicato la sua ingegnosità e la sua curiosità per proteggere le persone a lui vicine, e queste ultime lo hanno condannato per la sua sessualità.
La Macchina di Turing
La strada che ha portato Turing a definire il modello di calcolo oramai noto con il suo nome è, come tante strade umane, lunga, tortuosa, e affascinante.
Per capire appieno il motivo per cui Turing si è imbattuto nell'idea della macchina di Turing si dovrebbe iniziare dall'alba dell'umanità.
L'obiettivo finale della macchina di Turing infatti è lo studio dei processi automatici. Detto altrimenti,
il calcolo automatico
Questa strada in particolare è strettamente legata alla crisi dei fondamenti della matematica avvenuta agli inizi del \(1900\).
Data la complessità dell'argomento, rimando la trattazione ad un futuro video.
L'unica cosa importante da dire è che Turing stava cercando di risolvere un problema molto importante nel campo della logica matematica.
Il famoso paper del 1936 che introduce la macchina di Turing è noto con il nome di

Prima ancora di entrare nei dettagli matematici, Turing pone il lettore di fronte ad una situazione ben nota:
quella di una persona in procinto di eseguire un calcolo
Cosa succede, ad esempio, quando una persona sta cercando di calcolare la somma di due numeri?
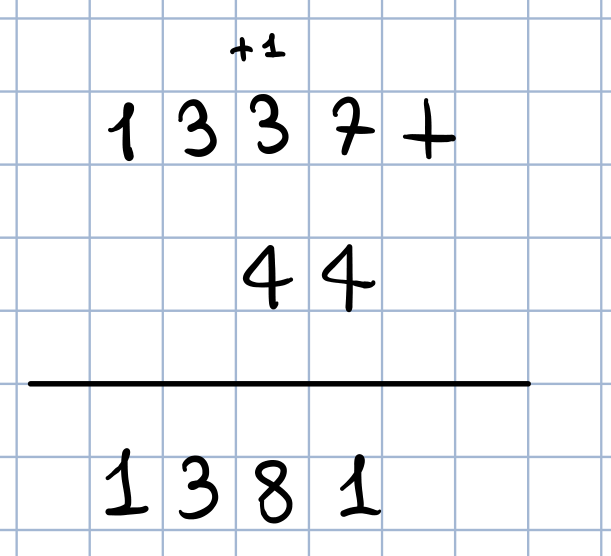
Osservazione: Un tempo la parola computer non si riferiva alle macchine, ma a degli esseri umani (tipicamente donne) il cui lavoro era quello di effettuare dei calcoli matematici molto difficili.
In altre parole,
Computer è ciò che calcola
Nel calcolo, Turing cattura i seguenti aspetti (1/3):
La persona, per lavorare, utilizza un pezzo di carta.
Su questa carta la persona può scrivere vari simboli.
In ogni momento del calcolo, la persona è in grado di leggere solo una porzione finita della carta su cui sta lavorando.
Nel calcolo, Turing cattura i seguenti aspetti (2/3):
In ogni momento del calcolo, la persona si troverà in un proprio stato interno.
Lo stato interno modifica come la persona reagisce alla visione di determinati simboli.
Nel calcolo, Turing cattura i seguenti aspetti (3/3):
A seconda di ciò che vede, e a seconda del proprio stato interno, la persona può decidere di:
- Cambiare il proprio stato interno.
- Scrivere un nuovo simbolo sul pezzo di carta, eventualmente sostituendo un simbolo precedentemente scritto.
- Cambiare la regione della carta su cui sta ponendo l'attenzione.
Notiamo che tutti questi aspetti sono puramente meccanici, nel senso che non fanno utilizzo né di intuizione e né di creatività.
Ed è proprio nel seguente passaggio che si trova la novità geniale introdotta da Turing:
Essendo meccanici, tutti questi passi possono potenzialmente essere effettuati da una macchina.
La carta è sostituita con un nastro diviso in celle, in cui in ogni cella può apparire un simbolo.
Su questa carta lavora una macchina con un proprio stato interno e una testina in grado di leggere, in ogni momento, un solo simbolo dal nastro.
A seconda dello stato interno e del simbolo letto, la macchina può decidere di cambiare stato interno, di scrivere un nuovo simbolo sul nastro, ed eventualmente di spostare la testina di un cella, a destra o a sinistra.
In questo modo, Turing sostituisce l'operatore umano con una macchina potenzialmente costruibile, facendo nascere a tutti gli effetti l'informatica teorica, intesa come lo studio teorico dei processi di calcolo automatici.

Definizione Matematica
Entriamo adesso nei dettagli matematici del modello.
Una macchina di Turing è definita come una sestupla
\[\langle \Sigma, \blacksquare, Q, q_0, Q_F, P \rangle\]
- \(\Sigma\) è un alfabeto di simboli.
- \(\blacksquare\) è il carattere blank.
- \(Q\) è un insieme di stati.
- \(q_0 \in Q\) è lo stato iniziale.
- \(Q_F \subseteq Q\) è l'insieme degli stati finali.
- \(P\) è la funzione di transizione
La parte più importante di una macchina di turing è la funzione di transizione \(P\)
\[P: (Q - Q_F) \times (\Sigma \cup \blacksquare) \longrightarrow Q \times (\Sigma \cup \blacksquare) \times \{\text{d}, \text{s}, \text{i}\}\]
Tale funzione infatti definisce le regole del comportamento della macchina. In altre parole, rappresenta il programma (software) implementato dalla particolare macchina di Turing.
Ciascuna regola in \(P\) è formata da \(5\) componenti:
\[(q, s) \longrightarrow (q^{'}, s^{'}, m)\]
Se la macchina si trova nello stato q e legge il simbolo s dal nastro, allora sovrascrive tale simbolo con il simbolo s', entra nel nuovo stato interno q' e fa il movimento descritto da m.
Esempio #1: somma unaria
Per capire meglio il funzionamento di queste macchine ho deciso di implementare un simulatore di macchine di Turing scritto in javascript.
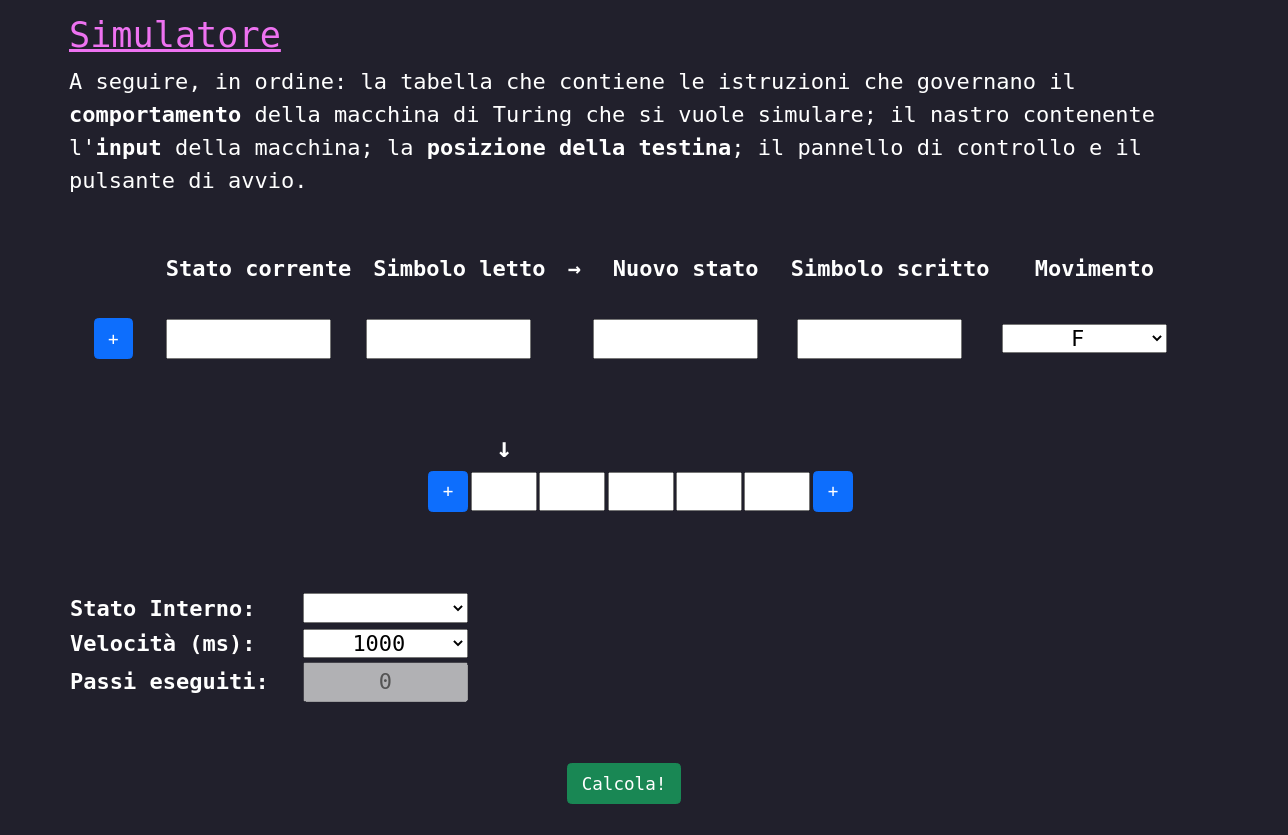
Ad esempio, consideriamo il problema di sommare due numeri scritti in unario, ovvero utilizzando un solo simbolo…
Esempio #2: somma binaria
Un problema assai più difficile da risolvere utilizzando una macchina di turing è il problema di sommare due numeri scritti in binario…
La difficoltà nel risolvere tale problema è conseguenza diretta del fatto che la macchina di Turing è un modello estremamente semplice di calcolo:
Potendo fare solamente poche cose, bisogna spezzare operazioni più complesse, come la somma di due numeri scritti in binario, in tantissime istruzioni più semplici.
Per questa ragione quando si scrivono degli algoritmi non si programma a livello delle quintuple, ma si utilizzano linguaggi più astratti.
Detto questo, tutto ciò che scriviamo in un qualsiasi linguaggio di programmazione può essere, in linea teorica, tradotto in delle quintuple di una macchina di Turing.
La Macchina Universale di Turing
Osserviamo a questo punto che
una singola macchina di Turing permette di risolvere un particolare problema computazionale
\[\begin{split} T_1 \longrightarrow P_1 \\ T_2 \longrightarrow P_2 \\ T_3 \longrightarrow P_2 \\ \end{split}\]
L'obiettivo di Turing nel suo paper del 1936 però non era la semplice definizione di una macchina di Turing.
Lui era interessato a dimostrare un risultato molto più generale:
Esistono problemi computazionali che non possono essere risolti in modi automatici
In un video precedente che ho fatto sul canale ho trattato proprio questo problema con tutti i dettagli matematici del caso.

Per raggiungere il suo obiettivo doveva quindi argomentare che la macchina da lui definita, ovvero la macchina di Turing, era in grado di catturare il concetto intuitivo di calcolabilità.
Turing voleva far capire al lettore che
Se un problema computazionale poteva essere risolto, allora esisteva una particolare macchina di Turing in grado di risolvere tale problema
E, viceversa,
Che se non esisteva una macchina di Turing in grado di risolvere un particolare problema computazionale, allora quel problema non poteva essere risolto in modo automatico
Questa tesi è stata poi formalizzata con il nome di Tesi di Church-Turing.
Per aiutare il lettore a capire questa tesi, Turing introduce la sua idea più bella di sempre:
la macchina universale di Turing
Mentre una macchina di Turing è in grado di risolvere un solo problema computazionale, come la calcolatrice è in grado di risolvere solamente problemi di tipo aritmetico, la macchina universale di Turing è "universale" nel senso che è in grado di
risolvere tutti i problemi computazionali che ammettono una soluzione automatica
Per fare questo l'idea geniale dietro alla macchina universale di Turing è la seguente:
Codificare le istruzioni di una qualsiasi macchina di Turing sotto forma di dati, ed interpretare queste istruzioni in modo da simulare il comportamento di quella particolare macchina.
In altre parole,
Dati ed istruzioni sono memorizzati nello stesso modo
In altre parole, la macchina universale \(U\) prende in input due cose:
- Le istruzioni \(P_T\) di un'altra macchina di Turing \(T\)
- I dati \(D_T\) in input alla macchina \(T\)
E, tramite questi dati, è in grado di simulare il comportamento di \(T\) sui dati \(D_T\).
Una volta costruita la macchina di turing \(U\), per modificarne il comportamento ci basta modificari i dati che passiamo in input alla macchina.
La macchina universale di Turing è uno dei primi esempi di macchina programmabile tramite del software.