Il Problematico Potere dei Simboli Sulla Mente Umana

I simboli ci ingannano

Cosa pensate quando vedete i seguenti simboli?

La maggior parte delle persone avrà sicuramente fatto la seguente associazione

Alcuni informatici potrebbero invece aver fatto quest'altra associazione.

Chi, dei due, ha ragione?

La persona comune, o l'informatico?

In realtà, nessuno dei due.

Qual è il problema?

Il fatto che la stessa sequenza di simboli (\(10\)) ha una quantita infinità di potenziali interpretazioni.

Ok, cerchiamo di capirci qualcosa.

La necessità dei simboli

Tra tutte le tecnologie scoperte dall'umanità, a partire dal fuoco e dagli strumenti costruiti con la pietra, il simbolo è forse stata la tecnologia più significativa di sempre.

Tramite il simbolo infatti l'essere umano è in grado di manipolare concetti tanto astratti quanto potenti.

Tra le tante cose, il simbolo ha permesso all'uomo di:

• Creare modelli della realtà ed utilizzare questi modelli per imporre (parzialmente) la propria volontà all'ambiente circostante.
• Gestire le informazioni, sempre in aumento, di società sempre più complesse.

Concentriamoci in particolare sul secondo punto:

la gestione delle informazioni.

Nelle società primitive le informazioni erano molto più semplici di quelle presenti nel modo moderno.

In ogni caso, la corretta gestione di tali informazioni era tanto critica quanto lo è tutt'ora.

La scrittura ha permesso all'uomo di inventare forse la più triste ma necessaria realtà: la burocrazia.

Tra i tanti compiti della burocrazia, c'è sicuramente anche quello di contare (scorte di cibo, quantità di armi, e via dicendo).

Per contare, è necessario inventare una notazione numerica, ovvero un modo per rappresentare delle quantità numeriche.

I numeri sono concetti intuitivi ed astratti, che eludono di mostrarsi direttamente.

Esempio: Non esiste un modo per far vedere esattamente che cos'è, ad esempio, il numero due.

Possiamo solo rappresentare tale numero in modo indiretto tramite dei simboli.

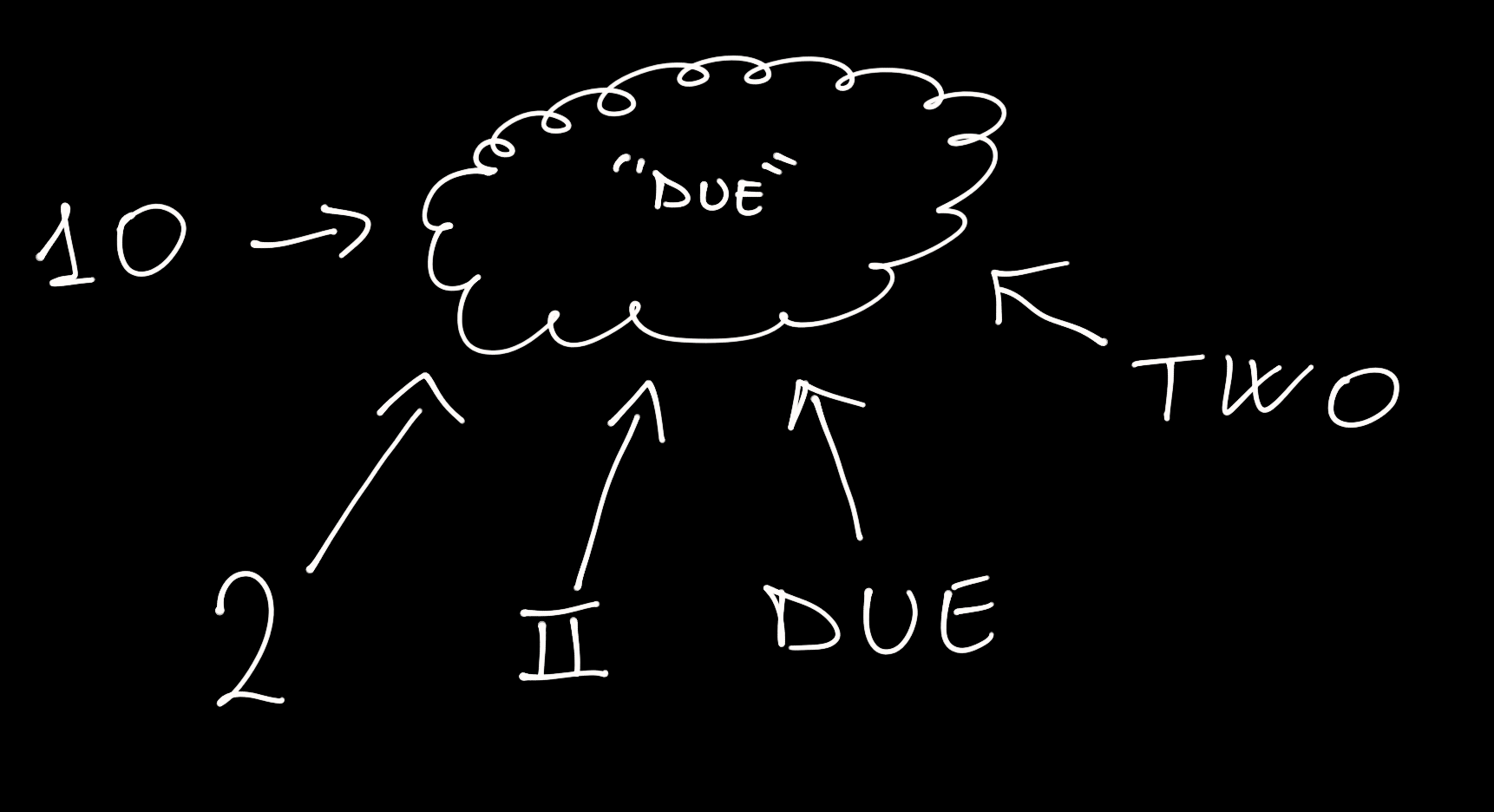
Detto altrimenti,

I numeri non possono essere visti, ma solo descritti.

Come possiamo creare una notazione che ci permetta di gestire e relazionare tra loro numeri sempre più grandi?

La notazione non-posizionale

Il modo in cui siamo stati abituati a scrivere i numeri non è per niente banale.

Consideriamo, ad esempio, il modo in cui i Romani scrivevano i numeri.

Notazione numerica dei Romani (1/5)

Avevano associato ad una serie di simboli delle quantità numeriche astratte.

\[\begin{split} \text{I} &\longrightarrow \text{numero uno} \\ \text{V} &\longrightarrow \text{numero cinque} \\ \text{X} &\longrightarrow \text{numero dieci} \\ \vdots \end{split}\]

Notazione numerica dei Romani (2/5)

Per esprimere numeri non direttamente esprimibili con un solo simbolo, concatenavano vari simboli tra loro fino a quando la somma dei valori associati ai vari simboli rifletteva il numero che si voleva rappresentare.

Notazione numerica dei Romani (3/5)

\[\begin{split} \text{III} &\longrightarrow \text{tre volte I} &\longrightarrow \text{numero tre} \\ \text{VV} &\longrightarrow \text{due volte V} &\longrightarrow \text{numero dieci} \\ \text{XXXX} &\longrightarrow \text{quattro volte X} &\longrightarrow \text{numero quaranta} \\ \end{split}\]

Notazione numerica dei Romani (4/5)

Nel corso del tempo sono state poi introdotte delle regole extra per semplificare la scrittura.

\[\begin{split} \text{IV} &\longrightarrow \text{numero quattro} \\ \text{IX} &\longrightarrow \text{numero nove} \\ \end{split}\]

Notazione numerica dei Romani (5/5)

In ogni caso, l'essenza del sistema di notazione utilizzato dai Romani per rappresentare i simboli è il fatto che

Il valore di ogni simbolo nell'interpretazione di un numero è sempre lo stesso, e non cambia rispetto alla posizione che il simbolo assume nella sequenza di simboli

Per questo motivo il sistema dei Romani è detto

non-posizionale.

E noi, invece?

Come scriviamo noi i numeri?

Che caratteristiche ha il nostro sistema di notazione numerica?

La notazione posizionale

Esattamente come hanno fatto i Romani, anche a noi ci è stato insegnato di associare a dei particolari simboli, delle particolari quantità numeriche astratte

\[\begin{split} \text{0} &\longrightarrow \text{numero zero} \;\;\; () \\ \text{1} &\longrightarrow \text{numero uno} \;\;\; (\circ)\\ \text{2} &\longrightarrow \text{numero due} \;\;\; (\circ \;\; \circ)\\ \vdots & \\ \text{9} &\longrightarrow \text{numero nove} \;\;\; (\circ \;\; \circ \;\; \ldots \;\; \circ \;\; \circ \;\; \circ) \\ \end{split}\]

Questi simboli sono dette cifre.

Sono due le caratteristiche che differenziano il nostro sistema di notazione da quello utilizzato dai romani:

• La presenza dello zero, indicato con \(0\).
• Il fatto che il valore delle cifre, ovvero il numero a cui la cifra fa riferimento, dipende dalla posizione che la cifra assume nella sequenza di simboli.

Nell'esempio che sta per seguire, dimentichiamoci di tutto e utilizziamo solamente ciò che ci viene insegnato nelle scuole elementari.

Esempio: Consideriamo i simboli \(1337\).

Se leggiamo tale sequenza da destra verso sinistra, abbiamo che la prima cifra è \(7\), mentre l'ultima è \(1\).

Notiamo che nel numero appare due volte la cifra \(3\).

Ma queste due occorrenze della stessa cifra, hanno lo stesso valore?

Esempio: Consideriamo i simboli \(1337\).

No, a scuola ci viene insegnato che le due occorrenze di \(3\) fanno riferimento a numeri diversi.

Abbiamo infatti la seguente associazione tra le cifre e i numeri associati a ciascuna cifra,

\[\begin{split} 7 &\longrightarrow \text{numero sette} \\ \text{(primo) } 3 &\longrightarrow \text{numero trenta} \\ \text{(secondo) } 3 &\longrightarrow \text{numero trecento} \\ 1 &\longrightarrow \text{numero mille} \\ \end{split}\]

Esempio: Consideriamo i simboli \(1337\).

Il numero associato all'intera sequenza di simboli è poi ottenuto sommando i numeri associati a ciascuna cifra.

\[\text{mille} + \text{trecento} + \text{trenta} + \text{sette}\]

Esempio: Consideriamo il numero \(1337\).

Simbolicamente siamo abituati a scrivere

\[\begin{split} 1337 &= 1000 + 300 + 30 + 7 \\ &= 1 \cdot 10^3 + 3 \cdot 10^2 + 3 \cdot 10^1 + 7 \cdot 10^0 \\ \end{split}\]

Come è possibile vedere, abbiamo espresso il nostro numero coma somma di potenze del numero dieci, in cui ciascuna potenza è moltiplicata per una delle cifra da \(0\) a \(9\).

Ok, facciamo un passo indietro.

Il problema più importante da risolvere quando vogliamo definire un sistema di notazione numerico deriva dal seguente fatto:

I simboli che possiamo utilizzare sono finiti, eppure i numeri che vogliamo rappresentare sono infiniti.

Come è possibile, utilizzando una quantità finita di simboli, rappresentare una quantità infinita di numeri?

Come conquistare l'infinito (in modo efficiente)

Come abbiamo già detto, i Romani, al fine di risolvere questo problema, hanno scelto di concatenare i simboli a disposizione, mantenendo però il valore di ogni simbolo costante rispetto alla posizione che il simbolo ha nella sequenza.

\[\text{XVX} \longrightarrow \text{dieci + cinque + dieci} = \text{venticinque}\]

Questo tipo di notazione funziona bene fin tanto che si vuole addizionare o sottrarre dei numeri, ma diventa difficile quando si vuole moltiplicare o dividere.

Analizziamo invece come funziona il nostro sistema di notazione dei numeri, supponendo di lavorare con le solite cifre Arabe.

\[0, \;\; 1, \,\; 2, \,\; 3, \;\; \ldots \;\; 8, \;\; 9\]

Per i numeri da \(\text{uno}\) a \(\text{nove}\), la traduzione è immediata, in quanto possiamo utilizzare proprio la cifra che rappresenta direttamente quel numero.

\[\begin{split} \text{0} &\longrightarrow \text{numero zero} \\ \text{1} &\longrightarrow \text{numero uno} \\ \text{2} &\longrightarrow \text{numero due} \\ \vdots & \\ \text{9} &\longrightarrow \text{numero nove} \\ \end{split}\]

Notiamo che le cifre possono essere ordinate tra loro:

• La \(0\) è il simbolo associato al numero più piccolo, che è proprio lo \(\text{zero}\).
• Poi viene la cifra \(1\), associata al successivo numero, il numero \(\text{uno}\).
• \(\ldots\)
• Alla fine abbiamo la cifra \(9\), associata al numero \(\text{nove}\).

\[ 0 < 1 < \ldots < 8 < 9\]

Come facciamo a rappresentare il numero \(\text{dieci}\), che viene subito dopo il numero \(\text{nove}\)?

Per il \(\text{nove}\) possiamo utilizzare l'ultima cifra a nostra disposizione.

\[9\]

E per il \(\text{dieci}\)?

L'idea è quella di ripartire dalla prima cifra, lo \(0\).

Dato però che abbiamo fatto un "giro completo", dobbiamo segnarci questo fatto, e quindi aggiungiamo una cifra che ci segna esattamente questo: "quanti giri completi per la prima posizione abbiamo fatto".

\[10\]

In questo caso, dato che per effettuare un giro completo abbiamo utilizzato esattamente \(\text{dieci}\) cifre, abbiamo la seguente, valida interpretazione

\[10 \longrightarrow \text{numero dieci}\]

In generale però, se avessimo utilizzato meno cifre (o più cifre), per effettuare un giro completo della prima posizione, allora la stessa sequenza di cifre (\(10\)), potrebbe non corrispondere al numero \(\text{dieci}\).

Questa è l'idea di base su cui poi si costruiscono i sistemi posizionali non decimali, tra cui troviamo:

• Il sistema binario.
• Il sistema ottale.
• Il sistema esadecimale.

Ma ritorniamo all'esempio di prima.

Ok, in questo caso particolare abbiamo che

\[10 \longrightarrow \text{numero dieci}\]

Come si continua a contare? Come rappresentiamo, ad esempio, il numero \(\text{undici}\), o il numero \(\text{dodici}\), e via dicendo?

L'idea è quella di utilizzare la prossima cifra disponibile rispetto alla posizione più a destra.

Troviamo dunque,

\[\begin{split} 10 &\longrightarrow \text{numero dieci} \\ 11 &\longrightarrow \text{numero undici} \\ 12 &\longrightarrow \text{numero dodici} \\ 13 &\longrightarrow \text{numero tredici} \\ 14 &\longrightarrow \text{numero quattordici} \\ 15 &\longrightarrow \text{numero quindici} \\ \end{split}\]

Continuando,

\[\begin{split} 15 &\longrightarrow \text{numero quindici} \\ 16 &\longrightarrow \text{numero sedici} \\ 17 &\longrightarrow \text{numero diciassette} \\ 18 &\longrightarrow \text{numero diciotto} \\ 19 &\longrightarrow \text{numero diciannove} \\ \end{split}\]

Notiamo che adesso abbiamo effettuato un altro giro completo. Nella posizione più a destra del numero siamo nuovamente arrivati alla cifra \(9\), l'ultima a nostra disposizione.

Come si continua?

Come al solito, si riparte da \(0\), ma prima si segna che si è fatto un altro giro completo andando a scegliere la prossima cifra disponibile per la posizione più a sinistra.

\[\begin{split} 19 &\longrightarrow \text{numero diciannove} \\ 20 &\longrightarrow \text{numero venti} \\ \end{split}\]

E di nuovo, tutto ciò si ripete…

\[\begin{split} 20 &\longrightarrow \text{numero venti} \\ 21 &\longrightarrow \text{numero ventuno} \\ 22 &\longrightarrow \text{numero ventidue} \\ \vdots \\ 29 &\longrightarrow \text{numero ventinove} \\ \end{split}\]

\[\begin{split} 29 &\longrightarrow \text{numero ventinove} \\ 30 &\longrightarrow \text{numero trenta} \\ \end{split}\]

Cosa succede quando facciamo un "giro completo" anche della posizione più a sinistra?

\[\begin{split} 99 &\longrightarrow \text{numero novantanove} \\ ? &\longrightarrow \text{numero cento} \\ \end{split}\]

L'idea è sempre la stessa:

Si pone a \(0\) la posizione più a destra, e, nella posizione situata alla sinistra di tale posizione, si va alla prossima cifra.

Dato però che in questo caso anche la posizione a sinistra è terminata, si pone a \(0\) anche questa, e si segna che si è fatto "un giro completo della seconda posizione" andando alla prossima cifra anche nella posizione alla sinistra di quella considerata.

\[\begin{split} 99 &\longrightarrow \text{numero novantanove} \\ 100 &\longrightarrow \text{numero cento} \\ \end{split}\]

(Alcuni) sistemi posizionali non decimali

Il sistema appena descritto è detto sistema di notazione posizionale a base dieci in quanto utilizza le tipiche dieci cifre Arabe.

\[0, \;\; 1, \,\; 2, \,\; 3, \;\; \ldots \;\; 8, \;\; 9\]

La base, in un sistema di notazione posizionale, è uguale al numero di simboli che abbiamo a disposizione per rappresentare una singola cifra

Il funzionamento di un sistema posizionale non necessita di utilizzare sempre la base dieci.

Possiamo utilizzare altre basi, ma il meccanismo sottostante sarà sempre lo stesso.

Lavorando in base \(\text{dieci}\):

\[\begin{split} &\_ \;\; &\_ \;\; &\_ \;\;\;|\;\;\;\;\; &\_ \;\; &1 \;\; &1 \;\;\;|\;\;\;\;\; &\_ \;\; &2 \;\; &2 \;\;\;|\;\;\;\;\; &1 \;\; &0 \;\; &2 \\ &\_ \;\; &\_ \;\; &0 \;\;\;|\;\;\;\;\; &\_ \;\; &1 \;\; &2 \;\;\;|\;\;\;\;\; &\_ \;\; &2 \;\; &3 \;\;\;|\;\;\;\;\; &1 \;\; &0 \;\; &3 \\ &\_ \;\; &\_ \;\; &1 \;\;\;|\;\;\;\;\; &\_ \;\; &1 \;\; &3 \;\;\;|\;\;\;\;\; &\_ \;\; &2 \;\; &4 \;\;\;|\;\;\;\;\; &1 \;\; &0 \;\; &4 \\ & \;\; &\vdots \;\; & \;\;\;\;\;\;\;\; &\;\; &\vdots \;\; & \;\;\;\;\;\;\;\; &\;\; &\vdots \;\; & \;\;\;\;\;\;\;\; &\;\; &\vdots \;\; & \\ &\_ \;\; &\_ \;\; &8 \;\;\;|\;\;\;\;\; &\_ \;\; &1 \;\; &9 \;\;\;|\;\;\;\;\; &\_ \;\; &9 \;\; &9 \;\;\;|\;\;\;\;\; &1 \;\; &0 \;\; &9 \\ &\_ \;\; &\_ \;\; &9 \;\;\;|\;\;\;\;\; &\_ \;\; &2 \;\; &0 \;\;\;|\;\;\;\;\; &1 \;\; &0 \;\; &0 \;\;\;|\;\;\;\;\; &1 \;\; &1 \;\; &0 \\ &\_ \;\; &1 \;\; &0 \;\;\;|\;\;\;\;\; &\_ \;\; &2 \;\; &1 \;\;\;|\;\;\;\;\; &1 \;\; &0 \;\; &1 \;\;\;|\;\;\;\;\; &1 \;\; &1 \;\; &1 \\ \end{split}\]

Il sistema binario (base due)

Nel sistema binario abbiamo solamente due simboli per rappresentari i nostri numeri.

\[0 \;\; , \;\; 1\]

Questo significa che il sistema binario è un sistema a base \(\text{due}\).

Troviamo quindi le seguenti associazioni:

\[\begin{split} 0 &\longrightarrow \text{numero zero} \\ 1 &\longrightarrow \text{numero uno} \\ 10 &\longrightarrow \text{numero due} \\ 11 &\longrightarrow \text{numero tre} \\ 100 &\longrightarrow \text{numero quattro} \\ 101 &\longrightarrow \text{numero cinque} \\ 110 &\longrightarrow \text{numero sei} \\ 111 &\longrightarrow \text{numero sette} \\ 1000 &\longrightarrow \text{numero otto} \\ \end{split}\]

Lavorando in base \(\text{due}\):

\[\begin{split} &\_ \;\; &\_ \;\; &\_ \;\; &\_ \;\;\;|\;\;\;\;\; &\_ \;\; &1 \;\; &0 \;\; &1 \;\;\;|\;\;\;\;\; &1 \;\; &0 \;\; &1 \;\; &1 \\ &\_ \;\; &\_ \;\; &\_ \;\; &0 \;\;\;|\;\;\;\;\; &\_ \;\; &1 \;\; &1 \;\; &0 \;\;\;|\;\;\;\;\; &1 \;\; &1 \;\; &0 \;\; &0 \\ &\_ \;\; &\_ \;\; &\_ \;\; &1 \;\;\;|\;\;\;\;\; &\_ \;\; &1 \;\; &1 \;\; &1 \;\;\;|\;\;\;\;\; &1 \;\; &1 \;\; &0 \;\; &1 \\ &\_ \;\; &\_ \;\; &1 \;\; &0 \;\;\;|\;\;\;\;\; &1 \;\; &0 \;\; &0 \;\; &0 \;\;\;|\;\;\;\;\; &1 \;\; &1 \;\; &1 \;\; &0 \\ &\_ \;\; &\_ \;\; &1 \;\; &1 \;\;\;|\;\;\;\;\; &1 \;\; &0 \;\; &0 \;\; &1 \;\;\;|\;\;\;\;\; &1 \;\; &1 \;\; &1 \;\; &1 \\ &\_ \;\; &1 \;\; &0 \;\; &0 \;\;\;|\;\;\;\;\; &1 \;\; &0 \;\; &1 \;\; &0 \;\;\;|\;\;\;\;\; &1 \;\; &0 \;\; &0 \;\; &0 \;\; 0 \\ \end{split}\]

Il sistema binario viene utilizzato nell'informatica per svariate ragioni.

Tra le tante, troviamo anche la seguente:

La diretta connessione tra le due cifre del sistema binario e i due possibili stati in cui si può trovare un circuito elettrico

\[\begin{split} 0 &\longrightarrow \text{la corrente NON passa} \\ 1 &\longrightarrow \text{la corrente passa} \\ \end{split}\]

Il sistema ottale (base otto)

Un altro sistema di notazione che viene molto spesso utilizzato nel mondo dell'informatica è quello ottale.

Il sistema di notazione ottale è caratterizzato dall'utilizzare \(\text{otto}\) simboli.

\[0, \;\; 1, \,\; 2, \,\; 3, \;\; 4, \;\; 5, \;\, 6, \;\; 7\]

Lavorando in base \(\text{otto}\):

\[\begin{split} &\_ \;\; &\_ \;\; &\_ \;\;\;|\;\;\;\;\; &\_ \;\; &1 \;\; &0 \;\;\;|\;\;\;\;\; &\_ \;\; &2 \;\; &1 \;\;\;|\;\;\;\;\; &1 \;\; &0 \;\; &2 \\ &\_ \;\; &\_ \;\; &0 \;\;\;|\;\;\;\;\; &\_ \;\; &1 \;\; &2 \;\;\;|\;\;\;\;\; &\_ \;\; &2 \;\; &2 \;\;\;|\;\;\;\;\; &1 \;\; &0 \;\; &3 \\ &\_ \;\; &\_ \;\; &1 \;\;\;|\;\;\;\;\; &\_ \;\; &1 \;\; &3 \;\;\;|\;\;\;\;\; &\_ \;\; &2 \;\; &3 \;\;\;|\;\;\;\;\; &1 \;\; &0 \;\; &4 \\ & \;\; &\vdots \;\; & \;\;\;\;\;\;\;\; &\;\; &\vdots \;\; & \;\;\;\;\;\;\;\; &\;\; &\vdots \;\; & \;\;\;\;\;\;\;\; &\;\; &\vdots \;\; & \\ &\_ \;\; &\_ \;\; &6 \;\;\;|\;\;\;\;\; &\_ \;\; &1 \;\; &6 \;\;\;|\;\;\;\;\; &\_ \;\; &7 \;\; &7 \;\;\;|\;\;\;\;\; &1 \;\; &0 \;\; &7 \\ &\_ \;\; &\_ \;\; &7 \;\;\;|\;\;\;\;\; &\_ \;\; &1 \;\; &7 \;\;\;|\;\;\;\;\; &1 \;\; &0 \;\; &0 \;\;\;|\;\;\;\;\; &1 \;\; &1 \;\; &0 \\ &\_ \;\; &1 \;\; &0 \;\;\;|\;\;\;\;\; &\_ \;\; &2 \;\; &0 \;\;\;|\;\;\;\;\; &1 \;\; &0 \;\; &1 \;\;\;|\;\;\;\;\; &1 \;\; &1 \;\; &1 \\ \end{split}\]

Ad esempio, per impostare i permessi di un file è possibile specificare una maschera di bit in formato ottale tramite il comando chmod

[leo@archlinux slides]$ touch new_file
[leo@archlinux slides]$ ls -lha new_file
-rw-r--r-- 1 leo users    0 22 nov 23.32 new_file

[leo@archlinux slides]$ chmod 565 new_file 
[leo@archlinux slides]$ ls -lha new_file 
  -r-xrw-r-x 1 leo users 0 22 nov 23.32 new_file

\[\begin{split} 565 &\longrightarrow \;\;\; &101 \;\; &110 \;\; &101 \\ &\longrightarrow \;\;\; &\text{r-x} \;\; &\text{rw-} \;\; &\text{r-x} \\ \end{split}\]

[leo@archlinux slides]$ chmod 777 new_file
[leo@archlinux slides]$ ls -lha new_file 
  -rwxrwxrwx 1 leo users 0 22 nov 23.32 new_file

\[\begin{split} 777 &\longrightarrow \;\;\; &111 \;\; &111 \;\; &111 \\ &\longrightarrow \;\;\; &\text{rwx} \;\; &\text{rwx} \;\; &\text{rwx} \\ \end{split}\]

Il sistema esadecimale (base sedici)

Un'altra base molto spesso utilizzata nell'informatica è la base sedici, caratterizzata dall'avere \(\text{sedici}\) simboli per rappresentare una cifra.

Per ottenere questo numero di simboli alle cifre arabe aggiungiamo le lettere dalla \(\text{A}\) alla \(\text{F}\), ordinate secondo il loro ordinamento lessicografico

\[\underbrace{0, \;\; 1, \,\; 2, \,\; 3, \;\; \ldots \;\; 9}_{\text{dieci simboli}} \;\; , \;\; \underbrace{\text{A}, \;\; \text{B}, \;\; \ldots \;\; \text{F}}_{\text{sei simboli}}\]

Lavorando in base \(\text{sedici}\):

\[\begin{split} &\_ \;\; &\_ \;\;\;&|\;\;\;\;\; &\_ \;\; &6 \;\;\;&|\;\;\;\;\; &\_ \;\; &D \;\;\;&|\;\;\;\;\; &1 \;\; &4 \;\;\;&|\;\;\;\;\; &1 \;\; &B \\ &\_ \;\; &0 \;\;\;&|\;\;\;\;\; &\_ \;\; &7 \;\;\;&|\;\;\;\;\; &\_ \;\; &E \;\;\;&|\;\;\;\;\; &1 \;\; &5 \;\;\;&|\;\;\;\;\; &1 \;\; &C \\ &\_ \;\; &1 \;\;\;&|\;\;\;\;\; &\_ \;\; &8 \;\;\;&|\;\;\;\;\; &\_ \;\; &F \;\;\;&|\;\;\;\;\; &1 \;\; &6 \;\;\;&|\;\;\;\;\; &1 \;\; &D \\ &\_ \;\; &2 \;\;\;&|\;\;\;\;\; &\_ \;\; &9 \;\;\;&|\;\;\;\;\; &1 \;\; &0 \;\;\;&|\;\;\;\;\; &1 \;\; &7 \;\;\;&|\;\;\;\;\; &1 \;\; &E \\ &\_ \;\; &3 \;\;\;&|\;\;\;\;\; &\_ \;\; &A \;\;\;&|\;\;\;\;\; &1 \;\; &1 \;\;\;&|\;\;\;\;\; &1 \;\; &8 \;\;\;&|\;\;\;\;\; &1 \;\; &F \\ &\_ \;\; &4 \;\;\;&|\;\;\;\;\; &\_ \;\; &B \;\;\;&|\;\;\;\;\; &1 \;\; &2 \;\;\;&|\;\;\;\;\; &1 \;\; &9 \;\;\;&|\;\;\;\;\; &2 \;\; &0 \\ &\_ \;\; &5 \;\;\;&|\;\;\;\;\; &\_ \;\; &C \;\;\;&|\;\;\;\;\; &1 \;\; &3 \;\;\;&|\;\;\;\;\; &1 \;\; &A \;\;\;&|\;\;\;\;\; &2 \;\; &1 \\ \end{split}\]

Tra i vari contesti in cui si utilizzano i numeri esadecimali, troviamo anche i seguenti:

1. Per specificare i colori (ad esempio nei formati RGB/RGBA).
2. Per specificare gli indirizzi di memoria.

    // RGBA, Red Green Blue Alpha
    #define BACKGROUND_COLOR 0x000000FF
    #define GRID_COLOR       0xFFFFFFFF
    #define SNAKE_COLOR      0xEE72F100

Source: Snake in C (ft. SDL2) – 8/10 (Gestione colori)

gdb -q ./hello
(gdb) b main
(gdb) run
(gdb) x/32wx $esp
0xffffd780:     0xffffd7a0      0x00000000      0x00000000      0xf7dc0a0d
0xffffd790:     0x00000001      0x56556060      0x00000000      0xf7dc0a0d
0xffffd7a0:     0x00000001      0xffffd844      0xffffd84c      0xffffd7d4
0xffffd7b0:     0xffffd7e4      0xf7ffdb78      0xf7f9b340      0xf7f91e1c
0xffffd7c0:     0x00000001      0x00000000      0xffffd828      0xffffffff
0xffffd7d0:     0xf7ffcfe0      0x00000000      0x00000001      0x56556060
0xffffd7e0:     0x00000000      0xb75a2888      0xf0e6ec98      0x00000000
0xffffd7f0:     0x00000000      0x00000000      0x00000001      0x56556060

Come (e dove) si scrive la base?

Abbiamo quindi capito che, prima di interpretare una sequenza di cifre per capire il numero a cui quelle cifre stanno facendo riferimento, abbiamo bisogno di capire la base utilizzata.

Nella quotidianità la base utilizzata è quasi sempre la base \(\text{dieci}\).

Questo, probabilmente, deriva dal fatto che abbiamo \(\text{due}\) mani, ciascuna delle quali possiede \(\text{cinque}\) dita.

\[\text{cinque} + \text{cinque} = \text{dieci}\]

Altre civiltà però nel corso della storia hanno utilizzato altre basi, o perché contavano utilizzando altre parti del corpo, oppure perché contavano le stesse parti del corpo ma in modo diverso.

Per togliere ogni ambiguità e favorire la corretta interpretazione di una sequenza di cifre, l'ideale sarebbe quello di specificare, assieme alla sequenza di cifre, anche la base utilizzata.

Ci sono vari modi per fare questo.

Si possono utilizzare determinati simboli per specificare determinate basi.

\[\text{0x} \longrightarrow \text{base sedici}\]

Si può scrivere il numero della base accanto al numero.

\[\begin{split} &(10)_{\text{base due}} &\longrightarrow \text{numero due} \\ &(10)_{\text{base dieci}} &\longrightarrow \text{numero dieci} \\ &(100)_{\text{base due}} &\longrightarrow \text{numero quattro} \\ &(100)_{\text{base dieci}} &\longrightarrow \text{numero cento} \\ \end{split}\]

Molto spesso la base è scritta utilizzando, implicitamente, la base \(\text{dieci}\) nel seguente modo

\[\begin{split} &(10)_{2} &\longrightarrow \text{numero due} \\ &(100)_{2} &\longrightarrow \text{numero quattro} \\ &(100)_{16} &\longrightarrow \text{numero duecentocinquantasei} \\ \end{split}\]

Come funziona in generale?

Adesso che abbiamo visto qualche esempio concreto, proviamo ad astrarre e cerchiamo di descrivere generalmente il funzionamento dei sistemi di notazione numerica posizionali.

La trattazione matematica delle proprietà di tali sistema è rimandata a futuri video.

In generale per lavorare con un sistema di notazione posizionale abbiamo bisogno di specificare la base \(b\) con cui vogliamo lavorare.

Il valore della base deve essere positivo, intero e \(b > 1\).

Una volta fissata la base \(b\) dobbiamo fissare i particolari simboli da associare ai numeri compresi tra \(0\) e \(b-1\).

\[\begin{split} &s_0 &\longrightarrow \text{numero zero} \\ &s_1 &\longrightarrow \text{numero uno} \\ &s_2 &\longrightarrow \text{numero due} \\ &\vdots \\ &s_{b-2} &\longrightarrow \text{numero } b - 2\\ &s_{b-1} &\longrightarrow \text{numero } b - 1\\ \end{split}\]

A questo punto tramite l'algoritmo di divisione euclidea siamo in grado di scrivere qualsiasi numero in questa base.

L'algoritmo verrà trattato in un video successivo.

Sia \(n\) il numero che vogliamo rappresentare.

Per una proprietà dimostrabile dei numeri interi, abbiamo che esistono sempre dei coefficienti tali che

\[n = c_l \cdot b^{l} + c_{l-1} \cdot b^{l-1} + \ldots c_1 \cdot b^1 + c_0 + b^0\]

con

\[c_0, c_1, \ldots, c_{l-1}, c_l \in \{0, \ldots, b - 1\}\]

Detto altrimenti,

possiamo rappresentare qualsiasi numero come una somma di potenze della base scelta \(b\).

Esempio: Possiamo rappresentare il numero \(\text{milletrecentotrentasette}\) in base \(\text{dieci}\) come la seguente somma di potenze della base

\[1 \cdot 10^3 + 3 \cdot 10^2 + 3 \cdot 10^1 + 7 \cdot 10^0\]

A questo punto, associamo a tale numero la seguente sequenza di simboli

\[1337 \longrightarrow \text{numero milletrecentotrentasette}\]

Le cifre arabe non sono speciali (e neanche arabe)

Notiamo che nella trattazione generale del sistema posizionale abbiamo assunto di lavorare con dei simboli generali \(s_0, \ldots, s_{b-1}\).

Questo significa che, per funzionare, il sistema posizionale non ha assolutamente bisogno di utilizzare le particolari cifre Arabe a cui siamo abituati.

In altre parole, non c'è nulla di speciale nei simboli

\[0, \;\; 1, \,\; 2, \,\; 3, \;\; \ldots \;\; 8, \;\; 9\]

ed è per convenzione e per motivi storici che oramai sono diventati così comuni e così utilizzati per rappresentari i numeri.

L'importante è avere un insieme finito di simboli distinguibili, e assegnare inizialmente a ciascuno di questi simboli un diverso intero compreso tra \(0\) e \(b-1\), dove \(b\) è la base scelta.

Conclusione

Dobbiamo stare attenti quando il nostro cervello in modo quasi automatico associa le cifre arabe ai numeri.

Durante questa associazione infatti il nostro cervello sta implicitamente utilizzando la base \(\text{dieci}\), perché questo è il modo in cui siamo sempre stati abituati a scrivere i numeri.

Questo può essere problematico, in quanto esistono vari contesti in cui la base utilizzata non è la la base \(\text{dieci}\).

Cosa fare quindi?

Bisogna avere pazienza e riflettere su ciò che si sta leggendo, in modo da poterlo interpretare correttamente.

Dunque, che cosa significa?

Dipende.

L'unica cosa che possiamo dire è che vediamo due simboli: il simbolo \(1\), e poi il simbolo \(0\).

Cosa significano questi simboli poi è tutta un'altra questione.