Cosa si studia all'università?

Introduzione

Avendo appena concluso il ciclo di studi Magistrale in informatica, vorrei provare a raccontare cosa significa in pratica studiare informatica all'università.

La laurea in informatica segue la tipica divisione 3/2:

• Si inizia con la laurea triennale:
  • tre anni di studio
  • totale di 180 CFU
• Si continua con la laurea magistrale:
  • due anni di studio
  • totale di 120 CFU

CFU? (1/2)

I CFU sono i Crediti Formativi Universitari, e vengono utilizzati per ottenere la laurea.

CFU? (2/2)

Ciascun corso, progetto o attività può erogare una diversa quantità di CFU a seconda del lavoro richiesto allo studente, sia in termine di difficoltà che in termine di tempo.

Un credito CFU corrisponde a 25 ore di lavoro.

Laurea Triennale in Informatica (1/5)

L'obiettivo principale della laurea triennale in informatica consiste nel fornire la conoscenza base e gli strumenti per poter iniziare a comprendere e sfruttare il potere del calcolo automatico.

Laurea Triennale in Informatica (2/5)

A tale fine vengono introdotti alcuni dei principali modelli matematici che permettono di ragionare in modo chiaro ed efficiente sui tipici problemi computazionali.

Laurea Triennale in Informatica (3/5)

Nasce dunque il bisogno di sviluppare la padronanza di vari linguaggi della matematica, tra cui troviamo anche:

Laurea Triennale in Informatica (4/5)

Vengono anche introdotti ed analizzati i linguaggi più propri dell'informatica, i linguaggi di programmazione:

Laurea Triennale in Informatica (5/5)

E i vari contesti tecnologici in cui questi ultimi vengono utilizzati:

Cerchiamo quindi di capirci qualcosa, iniziando dalle materie tipicamente trattare nel primo anno di una triennale in informatica:

\[\begin{align} \text{Analisi Matematica} \;\;&,\;\; \text{Matematica Discreta} \\ \text{Algebra Lineare} \;\;&,\;\; \text{Logica} \\ \text{Programmazione} \;\;&,\;\; \text{Architettura degli elaboratori} \\ \end{align}\]

Analisi Matematica

Analisi Matematica (1/7)

L'analisi matematica introduce lo studente allo studio dei numeri reali \(\mathbb{R}\) e in particolare al calcolo infinitesimale.

Analisi Matematica (2/7)

I tre macro-argomenti tipicamente affrontati sono:

Analisi Matematica (3/7)

Tipiche domande a cui il corso tenta di rispondere:

• Cosa differenzia i numeri reali dai numeri razionali?
• Perché \(\sqrt{2} \in \mathbb{R}\) è un numero reale?
• Come possiamo gestire sequenze infinite di numeri?

Analisi Matematica (4/7)

Calcolare il valore della seguente serie infinita:

\[1 + \frac{1}{2} + \frac{1}{4} + \ldots + \frac{1}{2^n} + \ldots = \sum_{i = 0}^{\infty} \frac{1}{2^i}\]

Analisi Matematica (5/7)

\[S = 1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \ldots\]

\[\frac{1}{2} S = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \ldots\]

Analisi Matematica (6/7)

\[\begin{split} S - \frac{1}{2} S &= 1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \ldots \\ &\;\;\; - \Big( \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \ldots \Big) \\ &= 1 \end{split}\]

Analisi Matematica (7/7)

\[S = \sum_{i = 0}^{\infty} \frac{1}{2^i} = 2\]

NOTA BENE: i calcoli appena esposti non sono assolutamente formali, e valgono solamente in particolari condizioni!

Matematica Discreta

Matematica Discreta (1/7)

La matematica discreta si pone l'obiettivo di analizzare tutte quelle strutture matematiche collegate all'insieme dei numeri naturali.

\[\mathbb{N} = \{0, 1, 2, 3, 4, \ldots\}\]

Matematica Discreta (2/7)

Sono tanti gli argomenti affrontati:

• Funzioni, Relazioni, Equivalenze
• Strutture algebriche
• Numeri Naturali e Induzione
• Aritmetica Modulare
• Scrittura posizionale
• Calcolo combinatorio
• Teoria dei numeri
• Algebre di Boole
• Teoria dei grafi

Matematica Discreta (3/7)

Tra i vari linguaggi della matematica, la matematica discreta è forse il linguaggio più importante per un informatico.

Nel mondo dei calcolatori digitali infatti tutto è discretizzato.

Matematica Discreta (4/7)

Definiamo un grafo \(G = (V, E)\) come una coppia di insiemi, dove:

• L'insieme \(V\) è detto insieme di nodi

  \[V = \{v_1, v_2, v_3 \}\]

• L'insieme \(E\) è detto insieme di archi

  \[E = \{(v_1, v_2), (v_2, v_3), (v_1, v_3)\}\]

Matematica Discreta (5/7)

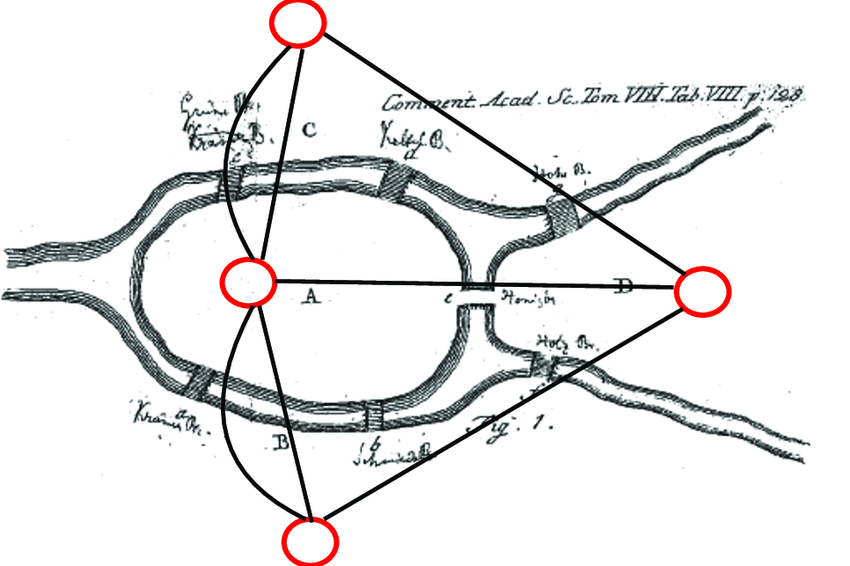
Königsberg bridges problem: È possibile trovare un cammino che percorre una e una sola volta tutti i ponti della cità di Königsberg e che finisce nello stesso posto in cui è iniziato?

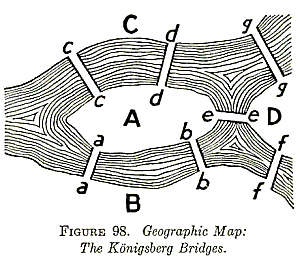
Matematica Discreta (6/7)

Risposta: No, non è possibile. (Leonhard Euler, 1736)

Matematica Discreta (7/7)

Per rispondere a tale domanda Euler ha modellato la città tramite un grafo.

Algebra Lineare

Algebra Lineare (1/3)

I principali oggetti di studio dell'algebra lineare sono gli spazi vettoriali, le applicazioni lineari e le matrici

\[\begin{bmatrix} 0 & 1 & 3 & 6 & 2 & 8\\ 1 & 3 & 5 & 6 & 8 & 9\\ 2 & 3 & 5 & 6 & 7 & 3\\ 2 & 1 & 5 & 9 & 10 & 11\\ \end{bmatrix}\]

Algebra Lineare (2/3)

Una delle prime operazioni che viene studiata sulle matrici è il prodotto tra matrici

\[\begin{bmatrix} 0 & 1 & 3 \\ 2 & 3 & 4 \\ 7 & 3 & 4 \\ \end{bmatrix} \cdot \begin{bmatrix} 0 & 2 & 1 \\ 3 & 1 & 5 \\ 8 & 0 & 0 \\ \end{bmatrix} = \begin{bmatrix} 27 & 1 & 5 \\ 41 & 7 & 17 \\ 41 & 17 & 22 \\ \end{bmatrix}\]

Algebra Lineare (3/3)

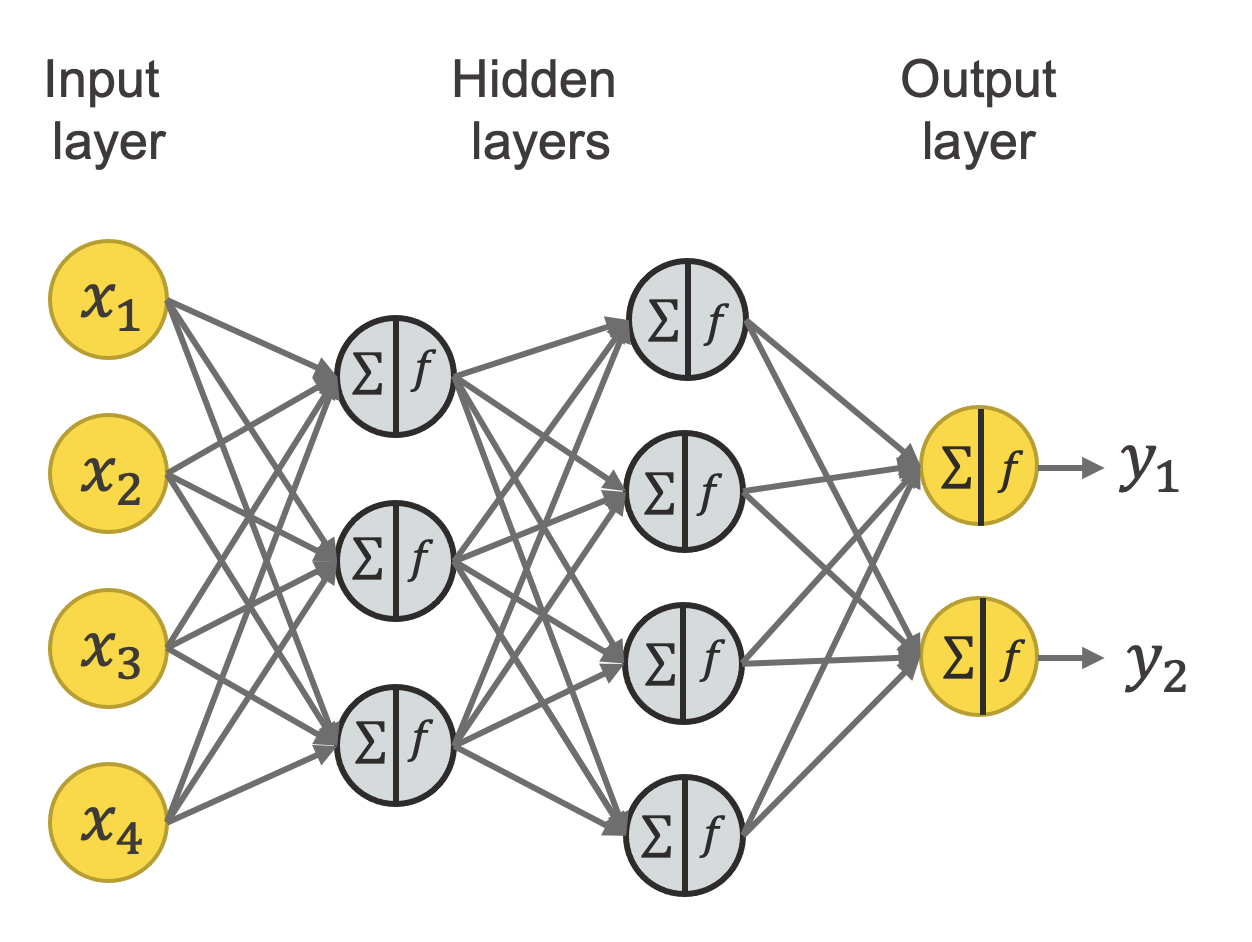
L'algebra lineare è utilizzata in moltissimi campi, tra cui il campo del machine learning e in particolare in tutti i modelli a reti neurali.

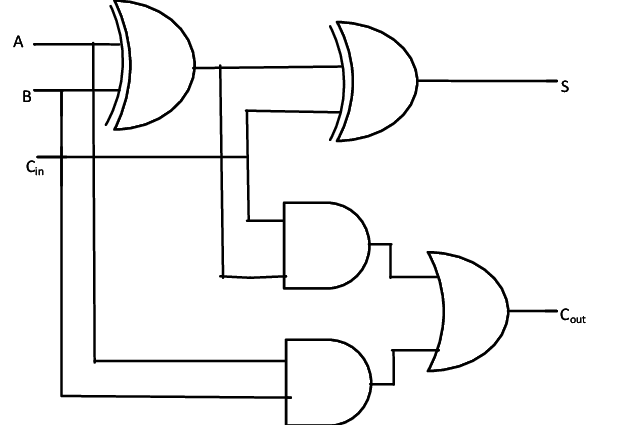
Logica e Reti Logiche

Logica (1/6)

La logica è forse lo strumento di calcolo più vecchio di sempre.

Lo studio della logica è dunque fondamentale, in quanto permette di codificare tramite un linguaggio formale alcune delle più importanti regole di ragionamento.

Logica (2/6)

Non solo, il linguaggio formale della logica può poi essere costruito nel mondo reale tramite l'utilizzo di circuiti digitali.

Logica (3/6)

Sono due i principali linguaggi analizzati in un corso introduttivo di logica:

• Logica proposizionale
• Logica del primo ordine

Logica (4/6)

Argomenti tipicamente trattati:

• Tautologie, contraddizioni
• Regole di inferenza
• Assiomi logici
• Sistemi formali
• Il ruolo dei quantificatori

Logica (5/6)

Classico sillogismo:

Socrate è un uomo.
Tutti gli uomini sono mortali.
-----------------------------
Socrate è mortale.

Logica (6/6)

Tradotto nella logica del primo ordine:

• \(\text{Uomo}(\text{socrate})\)
• \(\forall x: \;\; \text{Uomo}(x) \implies \text{Mortale}(x)\)

Implica

\[\text{Mortale}(\text{socrate})\]

Programmazione dei calcolatori

Programmazione (1/5)

L'obiettivo del primo corso di programmazione è quello di introdurre lo studente ai linguaggi di programmazione e a come utilizzare questi ultimi per strutturare delle computazioni.

Programmazione (2/5)

Tipicamente si sceglie un linguaggio tra

C, Python, Java

Programmazione (3/5)

A partire dal linguaggio scelto si introduce in modo progressivo la sintassi del linguaggio e la relativa semantica.

int risultato = -1;
if (condizione) {
  risultato = 5;
 } else {
  risultato = 10;
 }
printf("%d\n", risultato);

Programmazione (4/5)

Risolvendo vari problemi si comincia ad acquisire famigliarità con il linguaggio di programmazione studiato.

Programmazione (5/5)

Calcolo numeri di Fibonacci: \(F_n = F_{n-1} + F_{n-2}, \;\; F_1 = F_2 = 1\)

int fibo(int n) {
  int a = 1, b = 1, t = -1;

  if (n <= 2) { return 1; }

  for (int i = 2; i <= n; i++) {
    t = b;
    b = a + b;
    a = t;
  }

  return a;
}

Architettura degli elaboratori

Architettura (1/4)

L'obiettivo del corso di architettura è quello di studiare i concetti principali che si trovano alla base delle moderne architetture dei calcolatori.

In parole povere, si studia il modo in cui i computer sono strutturati al loro interno.

Architettura (2/4)

L'idea principale dietro alle moderne architetture è quella di costruire una serie di livelli di astrazione, in cui ciascun livello è costruito a partire dai servizi offerti dai livelli precedenti e offre a sua volta servizi ai livelli successivi.

Architettura (3/4)

Nei computer moderni troviamo i seguenti livelli:

Architettura (4/4)

Le porte logiche sono utilizzate per implementare operazioni quali la somma