Cosa si studia all'università?
Informatica Triennale, Overview Anno II
Introduzione
Nello scorso video avevo mostrato le principali materie che venivano studiate durante il primo anno di una laurea triennale in informatica.

Come avevamo visto, le materie trattavano principalmente la matematica e la logica di base.
\[\begin{align} \text{Analisi Matematica} \;\;&,\;\; \text{Matematica Discreta} \\ \text{Algebra Lineare} \;\;&,\;\; \text{Logica} \\ \text{Programmazione} \;\;&,\;\; \text{Architettura degli elaboratori} \\ \end{align}\]
Andiamo adesso a trattare le materie che vengono affrontare al secondo anno di studio.
Durante il secondo anno tipicamente vengono erogati vari corsi più incentrati su argomenti informatici, quali la programmazione, gli algoritmi, i sistemi operativi, i protocolli di rete e i database.
Le materie che ho affrontato durante il mio secondo anno sono state le seguenti:
- Algoritmi e Strutture Dati I
- Sistemi Operativi e Reti
- Linguaggi e Metodologie di Programmazione
- Basi di dati e di conoscenza
- Fondamenti di Informatica
- Calcolo delle Probabilità e Statistica
- Ricerca Operativa
Cerchiamo quindi di capirci qualcosa…
Algoritmi e Strutture Dati I
Algoritmi e Strutture Dati I (1/20)
L'obiettivo del corso di algoritmi e strutture dati I è quello di introdurre lo studente alle principali tecniche per la scrittura e l'analisi di algoritmi in grado di risolvere i più fondamentali problemi computazionali.
Algoritmi e Strutture Dati I (2/20)
Inizialmente vengono introdotti e definiti i concetti principali dietro alla risoluzione automatica di un problema.
Algoritmi e Strutture Dati I (3/20)
Tra questi argomenti troviamo anche i seguenti:
- Modello di calcolo.
- Algoritmo.
- Struttura dati.
- Complessità computazionale di un algoritmo.
- Analisi worst-case.
- Notazione asintotica.
Algoritmi e Strutture Dati I (4/20)
Successivamente si cominciano ad affrontare e risolvere i più classici problemi computazionali.
Durante la trattazione di questi specifici problemi si introducono le principali tecniche e metodologie per l'analisi e la scrittura degli algoritmi.
Algoritmi e Strutture Dati I (5/20)
Alcuni problemi affrontati:
- Il calcolo dei numeri di fibonacci.
- Il problema dell'ordinamento (Sorting).
- Il calcolo del cammino minimo (Shortest Path).
- Il calcolo del minimo albero ricoprente (MST).
- Il calcolo del taglio minimo (Min Cut).
Algoritmi e Strutture Dati I (6/20)
Per risolvere questi problemi si introducono e sviluppano le principali tecniche algoritmiche:
- Approccio Divide et Impera
- Approccio Greedy
- Approccio Dinamico
- Approccio Riduzionista
Algoritmi e Strutture Dati I (7/20)
E si introducono le principali strutture dati:
\[\begin{align} \text{Array} \;\;&,\;\; \text{Lista} \\ \text{Pila} \;\;&,\;\; \text{Coda} \\ \text{Coda di priorità} \;\;&,\;\; \text{Dizionario} \\ \end{align}\]
Algoritmi e Strutture Dati I (8/20)
Vediamo quindi come poter affrontare un piccolo problema…
Algoritmi e Strutture Dati I (9/20)
PROBLEMA: Abbiamo una bilancia a due piatti, e \(n \in \mathbb{N}\) monete. Una di queste monete è falsa, e dunque pesa di meno delle altre. Vogliamo capire con il numero minimo di pesate qual è la moneta falsa.

Algoritmi e Strutture Dati I (10/20)
Un primo approccio potrebbe essere quello di mettere la prima moneta su un piatto, e mettere tutte le altre monete sull'altro piatto, una alla volta.
Non appena notiamo una moneta più leggera dell'altra, sappiamo qual è quella falsa.
Algoritmi e Strutture Dati I (11/20)
Qual è il costo di questa soluzione?
Algoritmi e Strutture Dati I (12/20)
Se \(n\) sono le monete, e noi le proviamo dalla prima all'ultima, il costo dell'algoritmo è dato dal caso peggiore: quello in cui la moneta falsa è l'ultima moneta che proviamo.
In tal caso il costo è proprio
\[T(n) = O(n)\]
Algoritmi e Strutture Dati I (13/20)
Un secondo approccio potrebbe invece essere il seguente: divido le monete in due gruppi, e metto ciascun gruppo su un piatto diverso della bilancia.
Il piatto con il peso minore è proprio quello che contiene la moneta falsa. Posso quindi scartare l'altro gruppo ed effettuare la stessa operazione con il gruppo rimanente.
Algoritmi e Strutture Dati I (14/20)
Qual è il costo di quest'altra soluzione?
Algoritmi e Strutture Dati I (15/20)
Se \(n\) sono le monete, ad ogni pesata sto eliminando la metà delle possibilità, rimanendo solamente con \(n/2\) monete da controllare.
In totale quindi dovrò fare un numero logaritmico di pesate:
\[T(n) = O(\log_2{n})\]
Algoritmi e Strutture Dati I (16/20)
È questa la soluzione migliore che possiamo ottenere?
…NO!
Algoritmi e Strutture Dati I (17/20)
Un terzo approccio è il seguente: piuttosto che dividere solamente in due gruppi, possiamo dividere le monete in tre gruppi e procedere come segue:
- Se uno dei due gruppi messi sulla bilancia è più leggero dell'altro, allora la moneta si trova in quel gruppo.
- Altrimenti, se i due gruppi hanno lo stesso peso, la moneta si trova nel terzo gruppo che non abbiamo messo sulla bilancia.
Algoritmi e Strutture Dati I (18/20)
Qual è il costo di quest'altra soluzione?
Algoritmi e Strutture Dati I (19/20)
Se \(n\) sono le monete, ad ogni pesata sto eliminando due terzi delle possibilità, rimanendo solamente con \(n/3\) monete da controllare.
In totale,
\[T(n) = O(\log_3{n})\]
Algoritmi e Strutture Dati I (20/20)
Risorse potenzialmente utili:
Sistemi Operativi e Reti
Sistemi Operativi e Reti (1/21)
Il corso Sistemi Operativi e Reti è diviso in due parti:
- Nella prima parte si studiano le più importanti astrazioni software che sono state utilizzate nel corso degli anni per lo sviluppo dei sistemi operativi.
- Nella seconda parte si parla del funzionamento dei protocolli di rete, sia a livello hardware (accenni) che a livello software (approfondito), andando in particolare a discutere come funziona internet e il web.
Sistemi Operativi e Reti (2/21)
Per quanto riguarda la parte di sistemi operativi, sono affrontati anche i seguenti argomenti:
- Introduzione al concetto di sistema operativo.
- Evoluzione storica dei sistemi operativi.
- Gestione dei processi.
- Gestione della memoria.
- Gestione dell'I/O.
- Gestione del file system.
- Caso di studio: Unix e Linux.
Sistemi Operativi e Reti (3/21)
Per quanto riguarda la parte di reti, sono affrontati anche i seguenti argomenti:
- Che cos'è un protocollo di rete.
- Commutazione di pachetto e commutazione circuito.
- Il modello ISO/OSI.
- Data Link Layer (MAC).
- Network Layer (IP).
- Transport Layer (TCP/UDP).
- Application Layer (HTTP, FTP, SMTP, IMAP, DNS).
Sistemi Operativi e Reti (4/21)
Seguire il corso di sistemi operativi è fondamentale, in quanto ci permette di capire meglio cosa sta veramente succedendo quando scriviamo un programma.
Perché anche il programma più semplice può nascondere una immensa complessità.
Sistemi Operativi e Reti (5/21)
Cosa succede ad esempio quando andiamo a stampare a schermo in un programma C?
#include <stdio.h>
int main(void) {
printf("Hello World!\n");
return 0;
}
Sistemi Operativi e Reti (6/21)
Notiamo, come prima cosa, che possiamo compilare il programma tramite un altro programma: la shell.
[leo@archlinux code]$ echo ${BASH_VERSION}
5.1.16(1)-release
[leo@archlinux code]$ ls
os_example.c
[leo@archlinux code]$ gcc os_example.c -ggdb -o os_example
[leo@archlinux code]$ ls
os_example os_example.c
[leo@archlinux code]$ ./os_example
Hello World!
[leo@archlinux code]$
Sistemi Operativi e Reti (7/21)
Ma cosa sta facendo veramente la printf?
Resource: https://www.maizure.org/projects/printf/
Sistemi Operativi e Reti (8/21)
Il flusso operativo, molto approssimato, è il seguente:
- La printf chiama una funzione interna definita nella libreria standard C (libc).
- La libc si interfaccia con il kernel del sistema operativo sottostante per richiedere una stampa a schermo.
- Il kernel si interfaccia con il driver del dispositivo hardware su cui stampare la stringa richiesta.
- Il driver effettua la stampa sul dispositivo.
Sistemi Operativi e Reti (9/21)
Possiamo ottenere più informazioni su questi punti di interfacciamento tra un sistema e un altro tramite l'utilizzo di vari tools, tra cui troviamo:
strace, ldd, gdb
Sistemi Operativi e Reti (10/21)
Tramite strace ad esempio possiamo capire quali sono le system calls che vengono effettuate dal binario.
Le system calls (chiamate di sistema), sono i punti di interfacciamento tra il lato applicativo del sistema operativo e il kernel, che rappresenta il cuore del sistema operativo.
Sistemi Operativi e Reti (11/21)
Esempio strace
[leo@archlinux code]$ strace ./os_example
execve("./os_example", ["./os_example"], 0x7ffcba26b590 /* 39 vars */) = 0
...
write(1, "Hello World!\n", 13Hello World!) = 13
exit_group(0) = ?
Sistemi Operativi e Reti (12/21)
Tramite ldd invece possiamo vedere le librerie dinamiche che vengono caricate durante l'esecuzione del binario.
L'utilizzo di librerie dinamiche permette la generazione di eseguibili di dimensione limitata, in quanto la maggior parte del codice per l'interfacciament con il sistema operativo è situato all'interno del file system.
Sistemi Operativi e Reti (13/21)
Esempio ldd
[leo@archlinux code]$ ldd os_example linux-vdso.so.1 (0x00007ffd97b99000) libc.so.6 => /usr/lib/libc.so.6 (0x00007f9fe3ac0000) /lib64/ld-linux-x86-64.so.2 => /usr/lib64/ld-linux-x86-64.so.2 (0x00007f9fe3d01000)
Sistemi Operativi e Reti (14/21)
Infine, tramite gdb possiamo effettuare il debugging del processo, andando a capire esattamente quali sono le istruzioni eseguite dalla CPU e qual è il contenuto della memoria del processo e dei registri della CPU ad ogni istante.
Sistemi Operativi e Reti (15/21)
Esempio gdb
[leo@archlinux code]$ gcc os_example.c -ggdb -o os_example [leo@archlinux code]$ gdb -q ./os_example Reading symbols from ./os_example... (gdb) b *main Breakpoint 1 at 0x1139: file os_example.c, line 3. (gdb) disass main Dump of assembler code for function main: 0x0000000000001139 <+0>: push %rbp 0x000000000000113a <+1>: mov %rsp,%rbp 0x000000000000113d <+4>: lea 0xec0(%rip),%rax # 0x2004 0x0000000000001144 <+11>: mov %rax,%rdi 0x0000000000001147 <+14>: call 0x1030 <puts@plt> 0x000000000000114c <+19>: mov $0x0,%eax 0x0000000000001151 <+24>: pop %rbp 0x0000000000001152 <+25>: ret End of assembler dump. (gdb) start
Sistemi Operativi e Reti (16/21)
Seguire il corso di reti è fondamentale, in quanto ci permette di capire meglio cosa sta veramente succedendo quando utilizziamo un programma che comunica con altri programmi utilizzando la rete.
Sistemi Operativi e Reti (17/21)
Ad esempio, cosa succede quando apriamo una pagina web con il browser?
Sistemi Operativi e Reti (18/21)
Per ottenere la pagina che visualizziamo, il browser, detto anche il client, comunica con un web server tramite il protocollo HTTP al fine di scambiarsi risorse di tipo html, css e javascript.
Sistemi Operativi e Reti (19/21)
Per effettuare una richiesta HTTP possiamo utilizzare curl
[leo@archlinux ~]$ curl -v https://academy.leonardotamiano.xyz ... GET / HTTP/1.1 Host: academy.leonardotamiano.xyz User-Agent: curl/7.82.0 Accept: */* ...
Sistemi Operativi e Reti (20/21)
Nella risposta HTTP del server è presente il codice html che viene poi interpretato e visualizzato dal browser.
HTTP/1.1 200 OK Server: nginx Date: Sun, 31 Jul 2022 12:29:45 GMT Content-Type: text/html; charset=utf-8 Content-Length: 2282 Last-Modified: Fri, 08 Apr 2022 23:28:10 GMT Connection: keep-alive ETag: "6250c50a-8ea" Accept-Ranges: bytes
Sistemi Operativi e Reti (21/21)
Risorse potenzialmente utili:
- Teach Yourself Computer Science – Operating Systems
- Teach Yourself Computer Science – Networking
- Leonardo Tamiano – Web Servers (ft. Apache2)
- Leonardo Tamiano – Web Scraping con Python (ft. BeautifulSoup4)
- CS50 2017 - Lecture 6 - HTTP
- Hyper Text Transfer Protocol Crash Course - HTTP 1.0, 1.1, HTTP/2, HTTP/3
Linguaggi e Metodologie di Programmazione
Linguaggi e Metodologie di Programmazione (1/18)
Il corso di linguaggi e metodologie di programmazione si propone di analizzare i principali paradigmi di programmazione che sono stati scoperti e sviluppati nel corso degli anni.
Linguaggi e Metodologie di Programmazione (2/18)
Il corso si basa sull'osservazione che i linguaggi di programmazione non sono tutti uguali, e linguaggi diversi possono offrire diverse proprietà.
Linguaggi e Metodologie di Programmazione (3/18)
Ciascun linguaggio di programmazione in particolare può supportare uno o più paradigmi. Tra questi troviamo anche:
- Imperativo, procedurale (C)
- Imperativo, orientato agli oggetti (Java)
- Dichiarativo, funzionale (Haskel)
- Dichiarativo, logico (Prolog)
Linguaggi e Metodologie di Programmazione (4/18)
Nel paradigma procedurale il programmatore risolve il proprio problema andando a definire una serie di funzioni che operano su varie strutture dati.
Funzioni e strutture dati rimangono separate dal punto di vista del linguaggio, e il programmatore deve specificare esattamente come manipolare la struttura della memoria.
Linguaggi e Metodologie di Programmazione (5/18)
Esempio programmazione procedurale
#include <stdio.h>
int max(int a, int b) {
if (a > b) {
return a;
}
return b;
}
int min(int a, int b) {
return -max(-a, -b);
}
// ...
Linguaggi e Metodologie di Programmazione (6/18)
Nel paradigma orientato agli oggetti, il programmatore risolve il proprio problema andando a definire una gerarchia di classi che permettono poi di istanziare una serie di oggetti.
Funzioni e strutture dati continuano ad esistere, ma sono combinate assieme dal linguaggio nel concetto di classe.
Linguaggi e Metodologie di Programmazione (7/18)
Esempio programmazione orientata agli oggetti
package myproject;
public class Person {
private String name;
private int age;
public Person(String name, int age) {
this.name = name;
this.age = age;
}
public String greet() {
String out = "Hello, my name is " + this.name +
" , and my age is " + this.age;
return out;
}
public void setName(String name) { this.name = name; }
public void setAge(int age) { this.age = age; }
public String getName() { return this.name; }
public int getAge() { return this.age; }
}
Linguaggi e Metodologie di Programmazione (8/18)
Esempio programmazione orientata agli oggetti
package myproject;
public class Student extends Person {
public String matricola;
public Student(String name, int age, String matricola) {
super(name, age);
this.matricola = matricola;
}
public String getMatricola() {
return this.matricola;
}
public void setMatricola(String matricola) {
this.matricola = matricola;
}
}
Linguaggi e Metodologie di Programmazione (9/18)
Esempio programmazione orientata agli oggetti
import myproject.Person;
import myproject.Student;
public class Test {
public static void main(String[] args) {
Person p = new Person("Leonardo", 26);
System.out.println(p.greet());
Student s = new Student("Leonardo", 26, "1111");
System.out.println(s.getMatricola());
System.out.println(s.greet());
}
}
Linguaggi e Metodologie di Programmazione (10/18)
[leo@archlinux java]$ ls myproject Test.java [leo@archlinux java]$ ls myproject/ Person.class Person.java Student.class Student.java [leo@archlinux java]$ javac Test.java [leo@archlinux java]$ ls myproject Test.class Test.java [leo@archlinux java]$ java Test Hello, my name is Leonardo , and my age is 26 1111 Hello, my name is Leonardo , and my age is 26
Linguaggi e Metodologie di Programmazione (11/18)
Nel paradigma funzionale, il programmatore risolve il proprio problema andando a definire una serie di funzioni per poi comporle assieme.
Linguaggi e Metodologie di Programmazione (12/18)
Le funzioni, nel paradigma funzionale, cercano di essere il più possibili prive di side-effects, ovvero cercano di non modificare lo stato interno del programma, limitandosi a calcolare un output a partire da un input.
\[x \longrightarrow f(x) = y\]
Linguaggi e Metodologie di Programmazione (13/18)
PROBLEMA: leggere dallo standard input una sequenza di numeri separati da spazi, e stampare nello standard output la loro somma.
ESEMPIO INPUT : "1 2" --------> ESEMPIO OUTPUT: "3"
Linguaggi e Metodologie di Programmazione (14/18)
In Haskel la soluzione è la seguente
main = interact $ show . sum . map read . words
Compilando ed eseguendo..
[leo@archlinux code]$ ghc -dynamic functional.hs [leo@archlinux code]$ echo "1 2" | ./functional 3[leo@archlinux code]$
Linguaggi e Metodologie di Programmazione (15/18)
Infine troviamo il paradigma logico, in cui il programmatore risolve il proprio problema andando a definire una serie di predicati e una serie di fatti noti del mondo in modo da poter utilizzare il potere dell'inferenza logica.
Linguaggi e Metodologie di Programmazione (16/18)
Definiamo il predicato my_member(elem, list), che è vero se elem è un elemento contenuto nella lista list, altrimenti è falso.
my_member(X, [X | _]) :- !.
my_member(X, [_ | T]) :-
my_member(X, T).
Linguaggi e Metodologie di Programmazione (17/18)
Una volta definito il predicato possiamo effettuare delle query
my_member(1, [5, 3, 2]) % false
my_member(2, [5, 3, 2]) % true
my_member(5, [5, 3, 2]) % true
my_member(0, []) % false
Linguaggi e Metodologie di Programmazione (18/18)
Risorse potenzialmente utili:
Basi di Dati
Basi di Dati e di Conoscenza (1/31)
Il corso di basi di dati introduce lo studente alle principali metodologie e tecnologie che sono state sviluppate nel corso degli anni per affrontare tutti quei problemi legati alla
memorizzazione a lungo termine di dati.
Basi di Dati e di Conoscenza (2/31)
Un ingrediente fondamentale del progresso informatico infatti è sempre stato rappresentato dai dati.
Basi di Dati e di Conoscenza (3/31)
Se da una parte abbiamo gli algoritmi, intesi come sequenze di istruzioni, dall'altra abbiamo i dati, intesi come sequenze di bit.
\[\text{Algoritmi} \longleftrightarrow \text{Dati}\]
Basi di Dati e di Conoscenza (4/31)
I dati, dopo essere stati interpretati, diventano informazione, una delle risorse più preziose del mondo moderno.
\[\text{Algoritmi} \longleftrightarrow \text{Dati} \longleftrightarrow \text{Informazioni}\]
Basi di Dati e di Conoscenza (5/31)
Essere in grado di memorizzare in modo efficiente i dati a lungo termine diventa dunque un pre-requisito fondamentale per ogni tipo di analisi di dati.
A tale fine sono stati inventati i database.
Basi di Dati e di Conoscenza (6/31)
Che cos'è, quindi, un database?
Basi di Dati e di Conoscenza (7/31)
Possiamo descrivere un database come una collezione strutturata e persistente di dati.
Questa collezione è tipicamente salvata nella memoria fisica a lungo termine di un computer digitale.
Basi di Dati e di Conoscenza (8/31)
I software che ci permettono di gestire il database, sia dal punto di vista della memorizzazione interna che dal punto di vista dell'utilizzo sono chiamati DBMS (Database Management System).
Basi di Dati e di Conoscenza (9/31)
Questi software (DBMS) hanno vari compiti, tra cui:
- Memorizzano le informazioni garantendo varie e specifiche proprietà di persistanza e integrità ai dati.
- Permettono di modificare ed estrarre le informazioni salvate nel database tramite delle queries fornite dagli utenti.
Basi di Dati e di Conoscenza (10/31)
Consideramo un piccolo esempio…
Supponiamo di avere un insieme di utenti, e un insieme di prodotti. Ciascun utente può inserire nel proprio carrello uno o più prodotti.
Basi di Dati e di Conoscenza (11/31)
Il nostro obiettivo è definire un piccolo database che ci permetta di rispondere almeno alle seguenti domande:
- Dato un prodotto \(X\), quanti utenti hanno messo il prodotto \(X\) nel proprio carrello?
- Quanti oggetti ci sono nel carrello dell'utente \(Y\)?
- Qual è il prodotto più richiesto dai vari utenti?
Basi di Dati e di Conoscenza (12/31)
Notiamo come, prima di poter definire la struttura utilizzata per memorizzare i dati, dobbiamo avere bene a mente quali sono le informazioni che vogliamo estrarre da questi dati.
Basi di Dati e di Conoscenza (13/31)
Consideriamo come prima cosa i dati relativi agli utenti. Possiamo assumere che per ogni utente abbiamo a disposizione i seguenti dati:
- Un identificativo.
- Il nome dell'utente.
- La email dell'utente.
- La password dell'utente.
Basi di Dati e di Conoscenza (14/31)
L'idea quindi è quella di creare una tabella, le cui righe rappresentano i vari utenti, e in cui ciascuna riga è divisa in colonne, dove la singolla colonna rappresenta un particolare attributo o valore che associamo all'utente.
Basi di Dati e di Conoscenza (15/31)
Esempio tabella utenti:
| ID | nome | password | |
|---|---|---|---|
| 0 | leonardo | test@gmail.com | d3b0aa9cd8b72556… |
| 1 | daniele | test2.com | 3a30ef2f44440fb1… |
| … |
Basi di Dati e di Conoscenza (16/31)
Per andare a creare questa tabella (e più in generale l'intero database) possiamo utilizzare il linguaggio SQL.
\[\begin{split} \text{S} &\longrightarrow \text{Structured} \\ \text{Q} &\longrightarrow \text{Query} \\ \text{L} &\longrightarrow \text{Language} \\ \end{split}\]
Basi di Dati e di Conoscenza (17/31)
Codice SQL per creare la tabella utenti
CREATE TABLE users (
user_id INT NOT NULL AUTO_INCREMENT PRIMARY KEY,
name VARCHAR(50),
email VARCHAR(50),
password VARCHAR(256)
);
Basi di Dati e di Conoscenza (18/31)
Codice SQL per creare la tabella prodotti
CREATE TABLE products (
product_id INT NOT NULL AUTO_INCREMENT PRIMARY KEY,
description VARCHAR(250),
price INT
);
Basi di Dati e di Conoscenza (19/31)
Un concetto importante nello studio delle basi di dati è l'integrità referenziale, che è un vincolo che deve essere soddisfatto al fine di poter collegare righe di tabelle diverse in modo coerente.
Basi di Dati e di Conoscenza (20/31)
Codice SQL per creare la tabella carrello
CREATE TABLE cart (
cart_id INT NOT NULL AUTO_INCREMENT PRIMARY KEY,
user_id INT NOT NULL,
product_id INT NOT NULL,
FOREIGN KEY(product_id) REFERENCES products(product_id),
FOREIGN KEY(user_id) REFERENCES users(user_id)
);
N.B.: FOREIGN KEY!
Basi di Dati e di Conoscenza (21/31)
Avendo definito la struttura del database, possiamo andare ad inserire qualche dato di test.
INSERT INTO users
(name, email, password)
VALUES
("leonardo", "leonardo.test@gmail.com", "f053b3bb6f20c4aa101032cbea8dfa04bbf4855eded698d1716e07b9a289bca5"),
("daniele", "daniele.test@gmail.com", "d4a113c882db00ca0e4b547fb6a1e4ef0985158a720692c4bbc8cf25119e70be" ),
("giulia", "giulia.test@gmail.com", "bc5d6420d1a6f6b3b3194d397410a9ca8d7447f2c137d8a394780f416ebdf5af");
Basi di Dati e di Conoscenza (22/31)
Avendo definito la struttura del database, possiamo andare ad inserire qualche dato di test.
INSERT INTO products
(description, price)
VALUES
("processore CPU", 300),
("scheda GPU", 500),
("alimentatore", 100),
("ventola", 80);
Basi di Dati e di Conoscenza (23/31)
Avendo definito la struttura del database, possiamo andare ad inserire qualche dato di test.
INSERT INTO cart
(user_id, product_id)
VALUES
(1, 1),
(1, 2),
(2, 1),
(2, 3),
(2, 4),
(3, 2),
(3, 4),
(3, 1);
Basi di Dati e di Conoscenza (24/31)
Infine, siamo in grado di rispondere alle nostre domande iniziali.
Basi di Dati e di Conoscenza (25/31)
Query n. 1: Dato un prodotto \(X\), quanti utenti hanno messo il prodotto \(X\) nel proprio carrello?
SELECT users.user_id, name
FROM users, cart, products
WHERE users.user_id = cart.user_id AND
products.product_id = cart.product_id AND
products.description="scheda GPU";
Basi di Dati e di Conoscenza (26/31)
Query n. 1: Risultati…
+---------+----------+ | user_id | name | +---------+----------+ | 1 | leonardo | | 3 | giulia | +---------+----------+
Basi di Dati e di Conoscenza (27/31)
Query n. 2: Quanti oggetti ci sono nel carrello dell'utente \(Y\)?
SELECT count(*), users.name
FROM users, cart
WHERE users.user_id = cart.user_id and users.name="Leonardo";
Basi di Dati e di Conoscenza (28/31)
Query n. 2: Risultati…
+----------+----------+ | count(*) | name | +----------+----------+ | 2 | leonardo | +----------+----------+
Basi di Dati e di Conoscenza (29/31)
Query n. 3: Qual è il prodotto più richiesto dai vari utenti?
SELECT max(X.count), products.product_id, products.description
FROM (SELECT count(*) as count, product_id FROM cart GROUP BY product_id) as X, products
WHERE X.product_id = products.product_id;
Basi di Dati e di Conoscenza (30/31)
Query n. 3: Risultati…
+--------------+------------+----------------+ | max(X.count) | product_id | description | +--------------+------------+----------------+ | 3 | 1 | processore CPU | +--------------+------------+----------------+
Basi di Dati e di Conoscenza (31/31)
Risorse potenzialmente utili:
Fondamenti di Informatica
Fondamenti di Informatica (1/8)
Il corso di fondamenti di informatica introduce lo studente alla connessione tra macchine e linguaggi, e tra problemi e risorse computazionali.
Fondamenti di Informatica (2/8)
Le conoscenze sviluppate e introdotte in questo corso servono come basi per capire meglio le più fondamentali tecnologie che sono state sviluppate in ambito informatico nel contesto dei
linguaggi di programmazione.
Fondamenti di Informatica (3/8)
Si parla quindi di compilatori, interpreti, e in generale di tutti gli strumenti necessari alla creazione dei linguaggi di programmazione.
Fondamenti di Informatica (4/8)
Tra i vari argomenti sono trattati anche i seguenti:
- La Gerarchia dei linguaggi formali di Chomsky.
- Automi a stati finiti.
- Automi a pila.
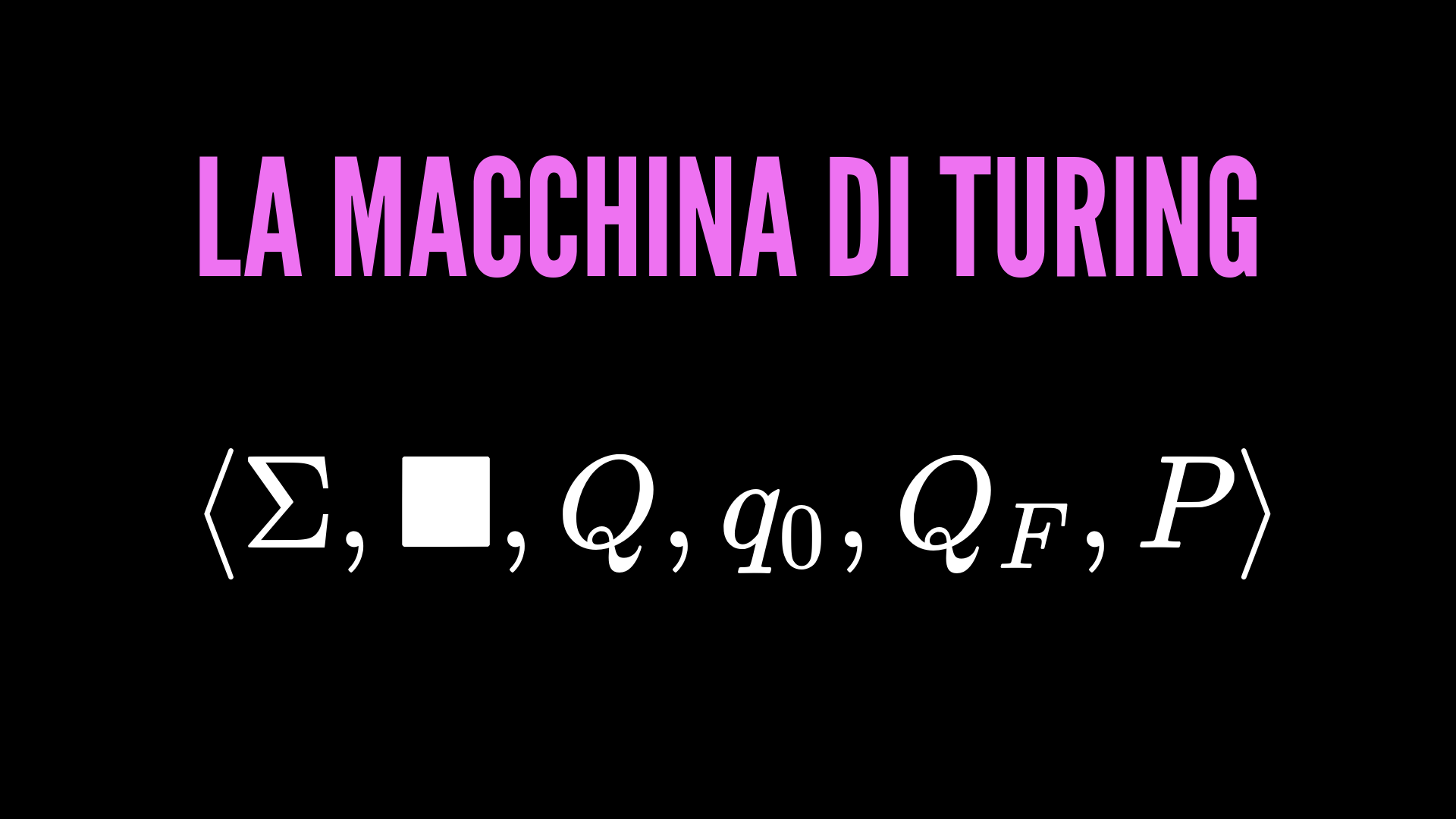
- Macchina di Turing.
- Problema della Fermata.
- Misure di complessità.
- Classe di complessità (P, NP, PSACE, …)
Fondamenti di Informatica (5/8)
Ho già trattato in un video precedente quali sono le connessioni tra le macchine e linguaggi:

Fondamenti di Informatica (6/8)
E anche che cos'è la Macchina di Turing:
Fondamenti di Informatica (7/8)
E come è stato risolto il Problema della Fermata:

Fondamenti di Informatica (8/8)
Verso la fine del corso si introduce una domanda fondamentale nella teoria della complessità
\[\text{P} \neq \text{NP}?\]
Calcolo delle Probabilità e Statistica
Calcolo delle Probabilità e Statistica (1/39)
Il corso di Calcolo delle Probabilità e Statistica introduce lo studente ai principali strumenti matematici offerti dai campi della probabilità e della statistica.
Calcolo delle Probabilità e Statistica (2/39)
Sia la probabilità che la statistica hanno a che fare con il concetto di randomicità.
Calcolo delle Probabilità e Statistica (3/39)
Ma che cos'è la randomicità (randomness) ?
Calcolo delle Probabilità e Statistica (4/39)
Definire esattamente che cos'è la randomness è una questione filosofica assai difficile e critica.
Detto questo, possiamo approcciare la situazione in modo più operativo e pragmatico.
Calcolo delle Probabilità e Statistica (5/39)
Consideriamo ad esempio il lancio di una moneta.

Quando lanciamo la moneta, non sappiamo esattamente se la moneta, una volta fermata, mostrerà la testa o la croce.
Calcolo delle Probabilità e Statistica (6/39)
Data la nostra incertezza sul predirre l'outcome futuro di questo evento, diciamo che l'evento è un evento randomico.
Calcolo delle Probabilità e Statistica (7/39)
In altre parole, la randomicità che associamo al lancio di una moneta è una diretta conseguenza della nostra ignoranza rispetto al risultato finale del lancio.
Calcolo delle Probabilità e Statistica (8/39)
Anche se non sappiamo predirre esattamente il risultato del lancio di una singola moneta, la teoria della probabilità offre dei modelli matematici in grado di analizzare cosa potrebbe succedere se lanciassimo più monete, una dopo l'altra.
Calcolo delle Probabilità e Statistica (9/39)
Cerchiamo quindi di modellare matematicamente il lancio di una moneta…
Calcolo delle Probabilità e Statistica (10/39)
Prima si definiscono gli eventi in gioco. Nel nostro caso abbiamo due eventi:
- L'evento \(T\), in cui la moneta esce tail (coda).
- L'evento \(H\), in cui la moneta esce head (testa).
Calcolo delle Probabilità e Statistica (11/39)
A ciascun evento viene poi associata una probabilità, dove la probabilità è modellata come un numero reale compreso tra \(0\) e \(1\).
\[p \in [0, 1] \subseteq \mathbb{R}\]
Calcolo delle Probabilità e Statistica (12/39)
Se ad un evento \(A\) associamo la probabilità
\[P(A) = 1\]
allora l'evento \(A\) succederà sempre in modo deterministico.
Calcolo delle Probabilità e Statistica (13/39)
Se ad un evento \(B\) associamo la probabilità
\[P(B) = 0\]
allora l'evento \(B\) non succederà mai in modo deterministico.
Calcolo delle Probabilità e Statistica (14/39)
Se ad un evento \(C\) associamo la probabilità
\[P(C) = \frac12\]
allora l'evento \(C\) succederà la metà delle volte.
Calcolo delle Probabilità e Statistica (15/39)
Nel caso del lancio della moneta quindi associamo le seguenti probabilità
\[\begin{split} P(T) &= p = \frac12\\ \\ P(H) &= q = 1 - p = \frac12\\ \end{split}\]
Calcolo delle Probabilità e Statistica (16/39)
Notiamo che
\[P(T) + P(H) = p + q = p + (1 - p) = \frac12 + \frac12 = 1\]
Calcolo delle Probabilità e Statistica (17/39)
Adesso che abbiamo modellato l'evento di base con le varie probabilità possiamo provare a rispondere alla seguente domanda:
Supponiamo di effettuare \(3\) lanci con una moneta equa uno dopo l'altro. Qual è la probabilità di ottenere \(2\) teste in totale?
Calcolo delle Probabilità e Statistica (18/39)
Per calcolare tale probabilità dobbiamo considerare tutti i casi possibili, e calcolare il rapporto tra il numero di casi favorevoli e il numero di casi totali.
Dato che ciascun lancio può avere \(2\) possibili risultati, e dato che facciamo \(3\) lanci di fila, otteniamo un totale di \(2^3 = 8\) possibilità.
Calcolo delle Probabilità e Statistica (19/39)
Le possibilità totali sono qui riportate
\[\begin{split} \text{HHH} \;&\;\; \text{TTT} \\ \text{HHT} \;&\;\; \text{TTH} \\ \text{HTH} \;&\;\; \text{THT} \\ \text{HTT} \;&\;\; \text{THH} \\ \end{split}\]
Calcolo delle Probabilità e Statistica (20/39)
Siamo quindi in grado di rispondere alla nostra domanda considerando il rapporto tra i casi favorevoli e i casi totali.
\[\frac{\text{casi favorevoli}}{\text{casi totali}} = \frac{3}{8} = 0.375\]
Calcolo delle Probabilità e Statistica (21/39)
Consideriamo adesso il problema più generale
Supponiamo di effettuare \(n\) lanci con una moneta equa uno dopo l'altro. Qual è la probabilità di ottenere \(k\) teste in totale?
con \(n, k \in \mathbb{N}^+\) e \(k \leq n\).
Calcolo delle Probabilità e Statistica (22/39)
Sia \(X\) il numero di teste ottenute in \(n\) lanci.
\[\begin{split} P(X = k) &= \binom{n}{k} \cdot p^k \cdot (1-p)^{n-k} \\ &= \binom{n}{k} \cdot p^n \\ &= \frac{n!}{k!(n-k)!} \cdot p^n \\ \end{split}\]
Calcolo delle Probabilità e Statistica (23/39)
Fissato \(n=10\), andando a calcolare la formula al variare di \(k\) otteniamo
[leo@archlinux python]$ python3 coin_toss.py P(X=0) = 0.0009765625 P(X=1) = 0.009765625 P(X=2) = 0.0439453125 P(X=3) = 0.1171875 P(X=4) = 0.205078125 P(X=5) = 0.24609375 P(X=6) = 0.205078125 P(X=7) = 0.1171875 P(X=8) = 0.0439453125 P(X=9) = 0.009765625 P(X=10) = 0.0009765625
N.B.: I valori più probabili sono intorno a \(k \approx n/2 = 5\)
Calcolo delle Probabilità e Statistica (24/39)
Il codice per il calcolo precedente
#!/usr/bin/env python3
import math
if __name__ == "__main__":
n = 10
p = 0.5
for k in range(0, n+1):
prob_value = math.comb(n, k) * pow(p, n)
print(f"P(X={k}) = {prob_value}")
Calcolo delle Probabilità e Statistica (25/39)
Mentre la probabilità cerca di trovare e studiare delle leggi matematiche precise, la statistica lavora direttamente con delle osservazioni empiriche al fine di ottenere informazioni sul particolare evento studiato.
Calcolo delle Probabilità e Statistica (26/39)
Nel contesto del lancio di una moneta…
Probabilità: Definisco parametro \(p\) e poi calcolo la probabilità di ottenere \(k\) teste in \(n\) lanci.
Statistica: Misuro quante volte in \(n\) lanci ottengo delle teste, e a partire da questo numero \(x\) provo a stimare il valore di \(p\).
Calcolo delle Probabilità e Statistica (27/39)
Supponiamo di avere una moneta, e di essere interessati a capire se la moneta è equa oppure no. In altre parole, vogliamo capire se \(p = 1/2\) oppure no.
Calcolo delle Probabilità e Statistica (28/39)
A tale fine possiamo prendere la moneta ed effettuare dei lanci.
L'idea è quella di misurare la differenza tra i dati ottenuti dalla nostra moneta e quelli che avremmo ottenuto se la moneta fosse equa.
Calcolo delle Probabilità e Statistica (29/39)
Codice per simulare \(m\) trials di \(n\) lanci di moneta con probabilità di cadere testa \(p\)
#!/usr/bin/env python3
import random
from pylab import bar
from pylab import show
if __name__ == "__main__":
n, m, p = 1000, 1000, 0.5
coin_tosses = [sum([random.random() < p for i in range(n)])
for j in range(m)]
frequencies = [coin_tosses.count(k) for k in range(n+1)]
bar(range(n+1), frequencies, align='center')
show()
Calcolo delle Probabilità e Statistica (30/39)
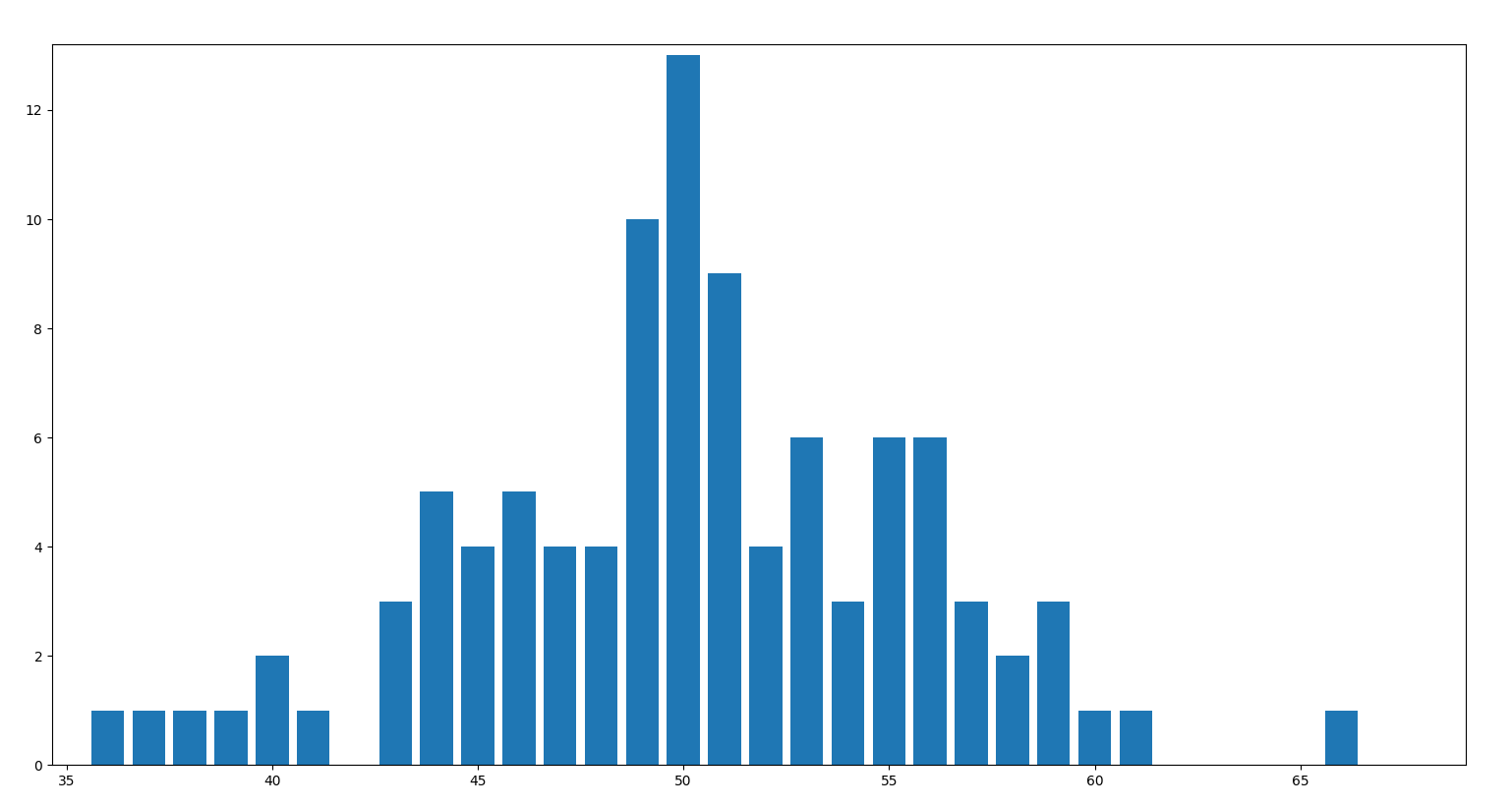
Per \(n=100\), \(m=100\) e \(p=0.5\) otteniamo
Calcolo delle Probabilità e Statistica (31/39)
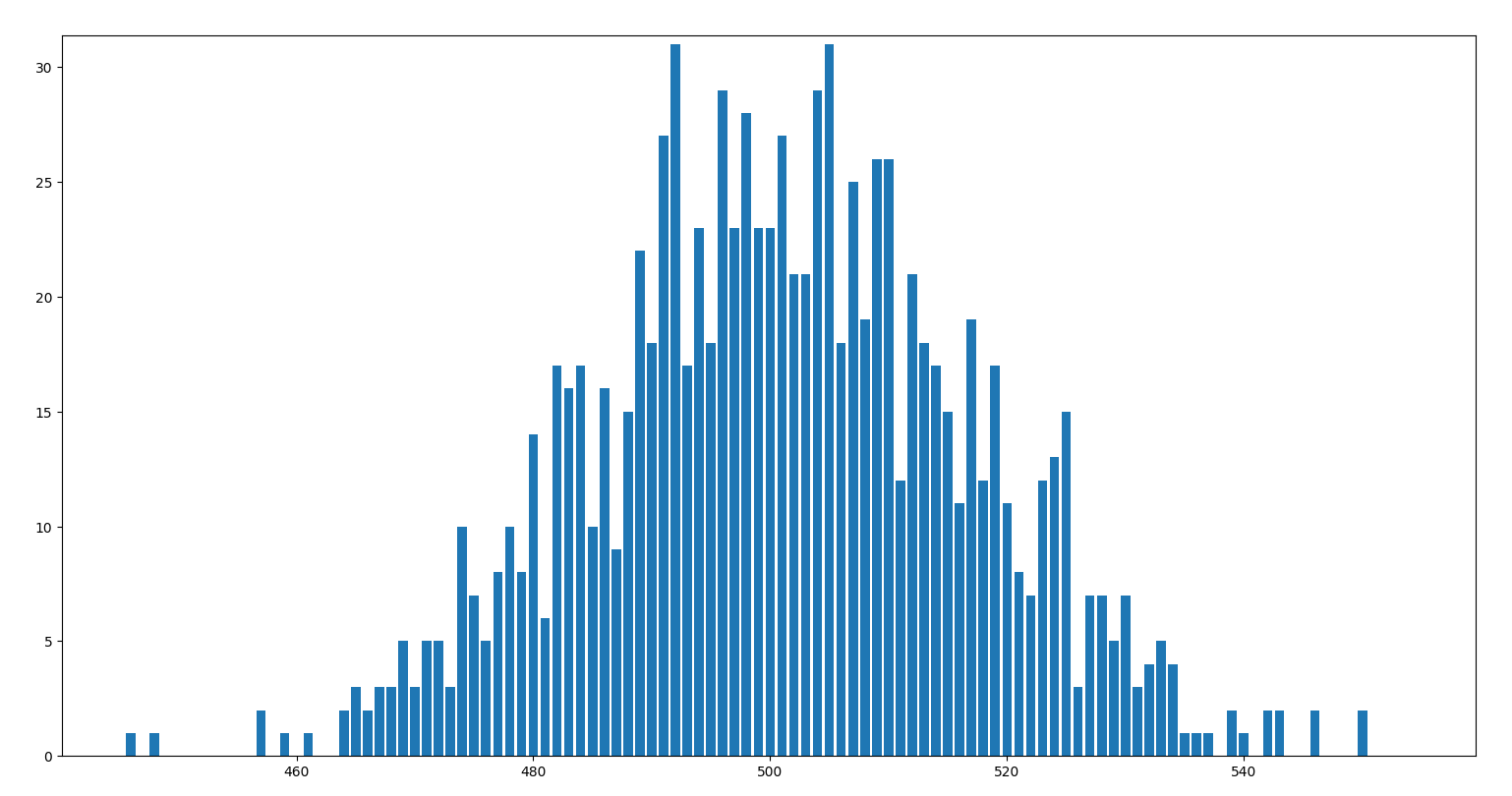
Per \(n=1000\), \(m=1000\) e \(p=0.5\) otteniamo
Calcolo delle Probabilità e Statistica (32/39)
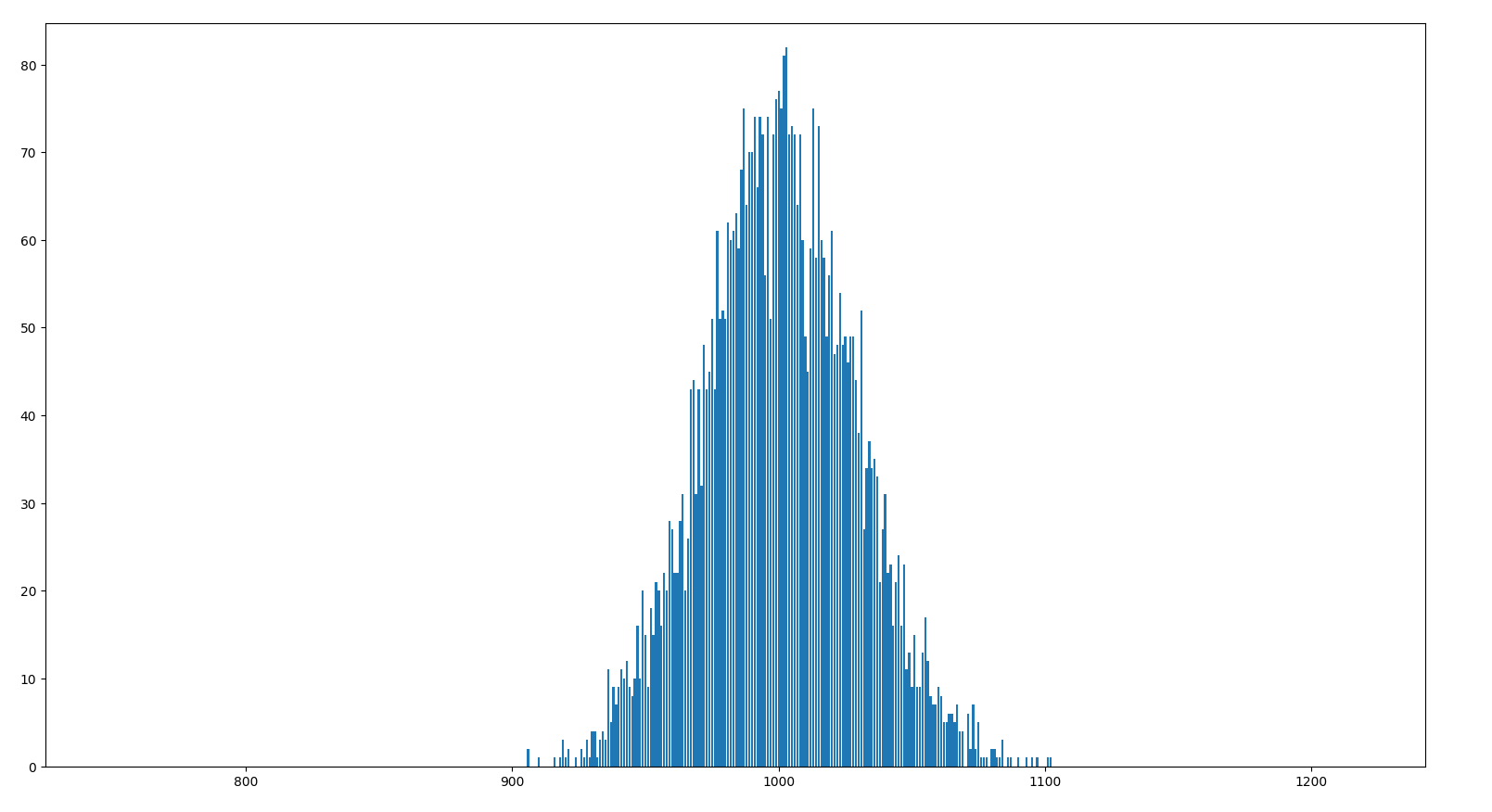
Per \(n=5000\), \(m=5000\) e \(p=0.5\) otteniamo
Calcolo delle Probabilità e Statistica (33/39)
Al crescere di \(n\) ed \(m\) otteniamo una figura sempre più simile alla seguente curva, detta curva normale o curva di Gauss.

Calcolo delle Probabilità e Statistica (34/39)
Osserviamo inoltre che per \(p=0.5\) la parte centrale della curva si trova sempre più o meno vicino \(n/2\).
Cosa succede invece se \(p \neq 0.5\)?
Calcolo delle Probabilità e Statistica (35/39)
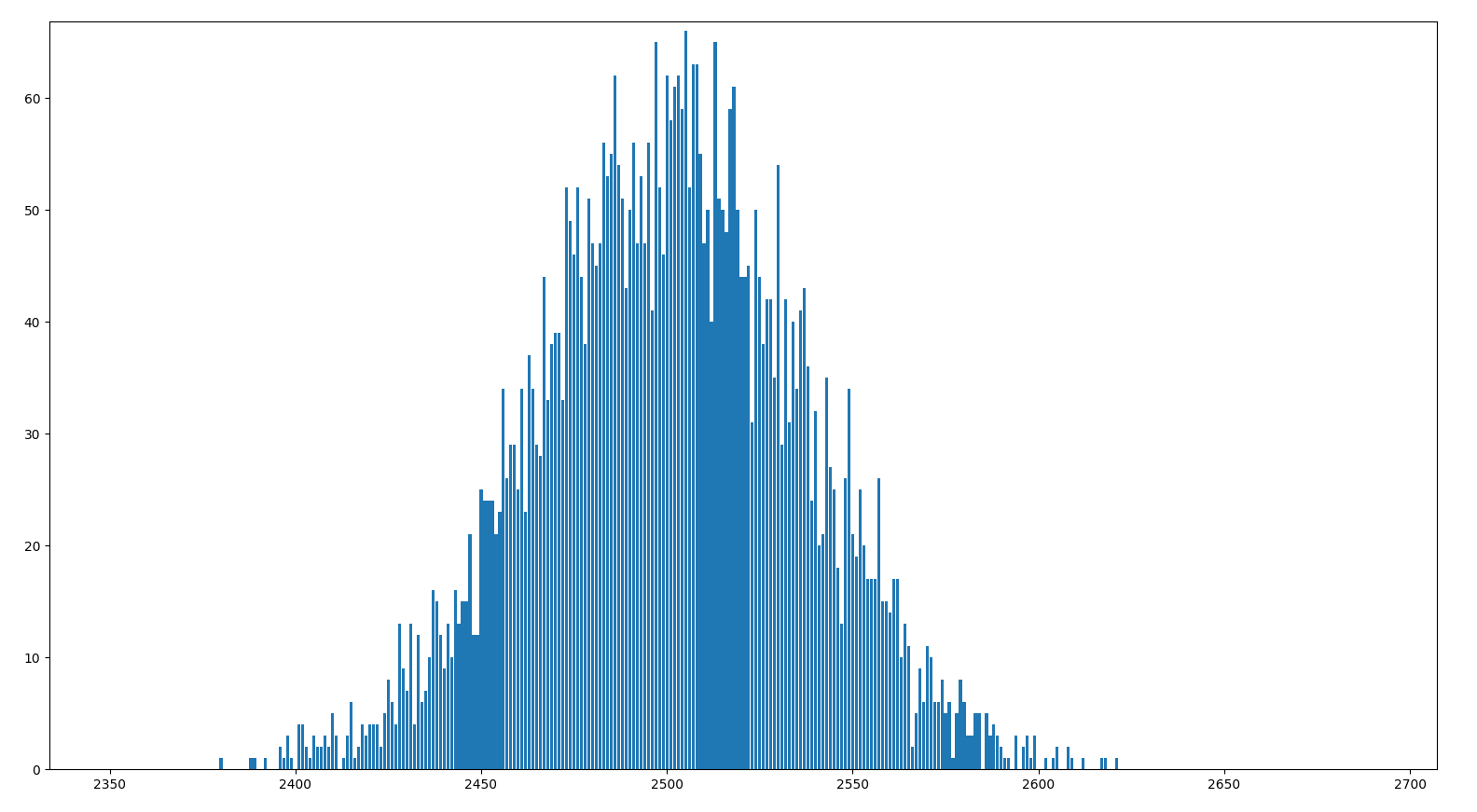
Per \(n=5000\), \(m=5000\) e \(p=0.2\) otteniamo
Calcolo delle Probabilità e Statistica (36/39)
Per \(n=5000\), \(m=5000\) e \(p=0.7\) otteniamo
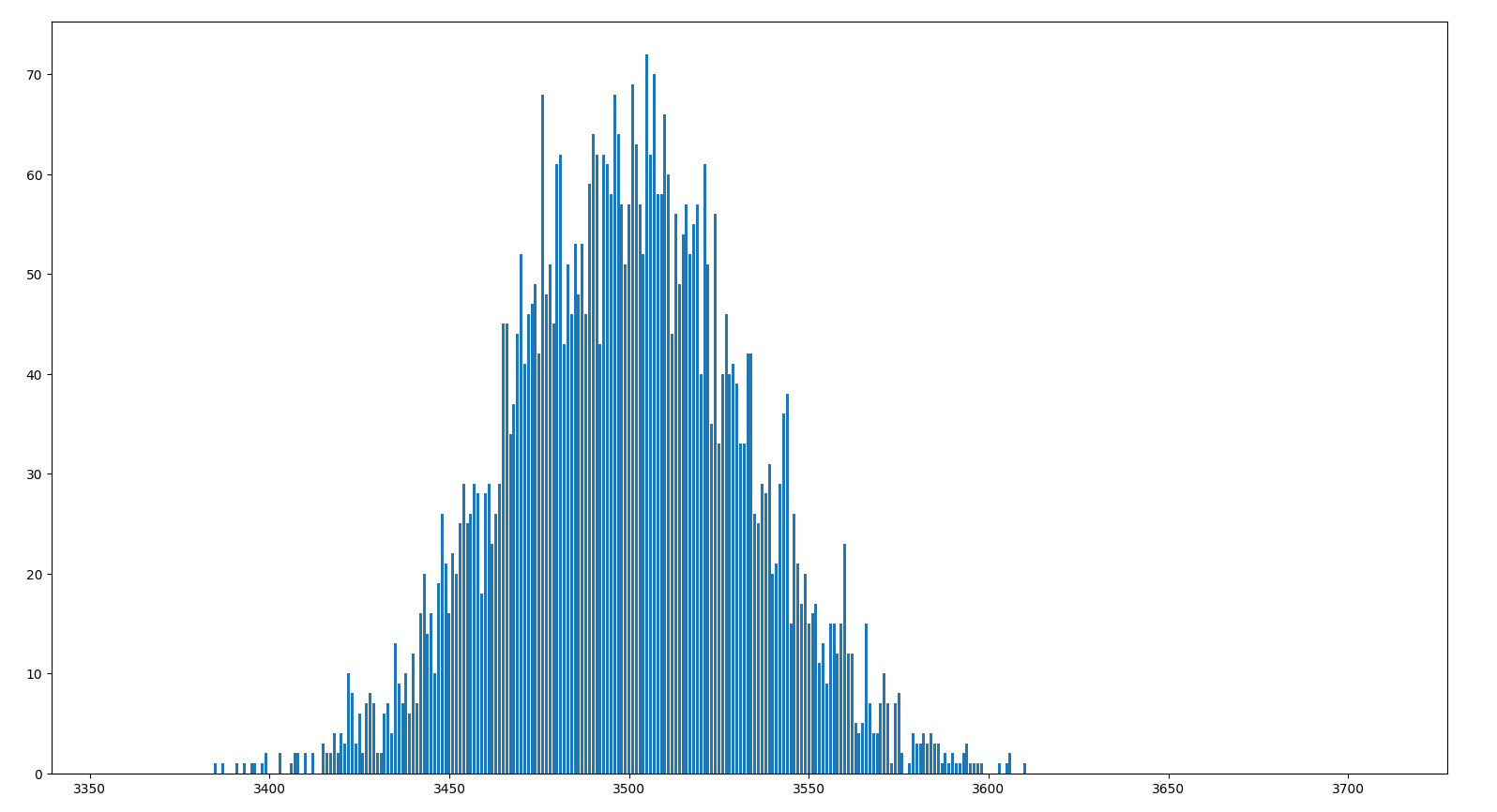
Calcolo delle Probabilità e Statistica (37/39)
Per \(n=5000\), \(m=5000\) e \(p \in \{0.2, 0.5, 0.7\}\)
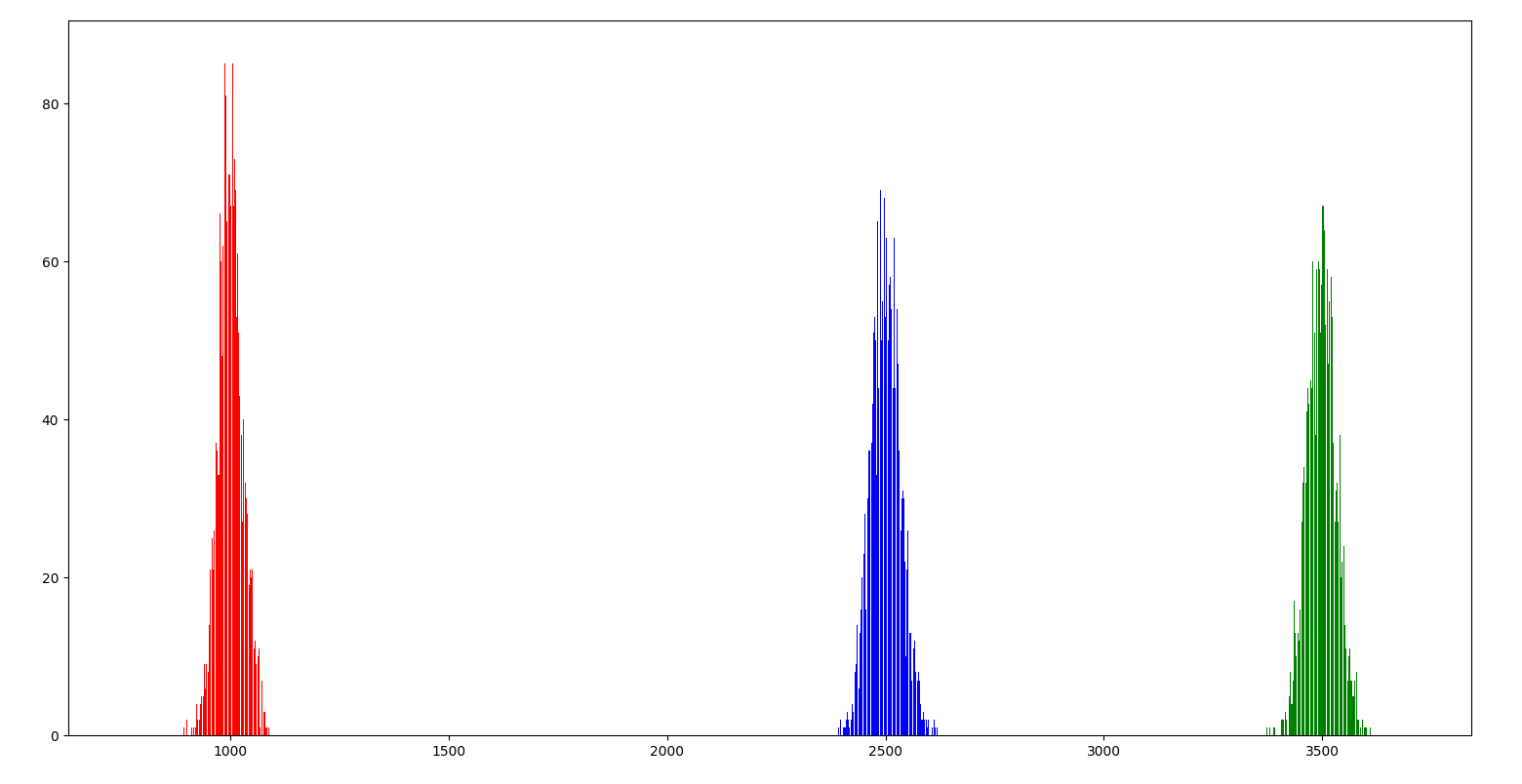
Calcolo delle Probabilità e Statistica (38/39)
A seconda della posizione della curva possiamo capire se la moneta è bilanciata oppure no:
- Vicino al centro, la moneta è bilanciata, e \(p \approx 1/2\).
- Tendende verso sinistra, \(p \ll 1/2\), la moneta tende a dare più croce che testa.
- Tendende verso destra, \(p \gg 1/2\), la moneta tende a dare più testa che croce.
Calcolo delle Probabilità e Statistica (39/39)
Risorse potenzialmente utili:
Ricerca Operativa
Ricerca Operativa (1/12)
Il corso di ricerca operativa introduce i principali algoritmi e tecniche per la trattazione di problemi di ottimizzazione lineari con vincoli lineari.
Ricerca Operativa (2/12)
Abbiamo un problema di ottimizzazione quando dobbiamo massimizzare o minimizzare una data funzione
\[f:\mathbb{R}^n \to \mathbb{R}\]
Ricerca Operativa (3/12)
Se poi la funzione è lineare allora abbiamo un problema di ottimizzazione lineare.
Ricerca Operativa (4/12)
Esempi di funzioni lineari:
\[\begin{split} f(x, y) &= 10x + 20y \\ f(x, y, z) &= 100x + 200y + 50z \\ \end{split}\]
Ricerca Operativa (5/12)
I vincoli lineari invece sono espressi tramite delle disequazioni lineari della forma
\[\begin{split} x + y &\leq 50 \\ x &> 0 \\ y &> 0 \\ \end{split}\]
Ricerca Operativa (6/12)
In generale quindi un tipico problema affrontato dalla programmazione lineare è così espresso:
La funzione da massimizzare è
\(f(x, y) = 180x + 200y\)
I vincoli con cui lavoriamo sono
\[\begin{split} 5x + 4y \leq 80 \;\;\;&,\;\; 10x + 20y \leq 200\\ x \geq 0 \;\;\;&,\;\; y \geq 0\\ \end{split}\]
Ricerca Operativa (7/12)
Se andiamo a visualizzare la regione del piano che rispetta i vincoli del problema, otteniamo la seguente immagine.
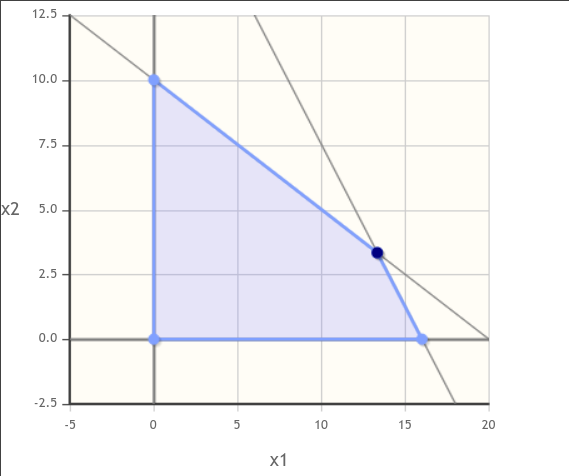
Ricerca Operativa (8/12)
Il valore della soluzione è
\[\begin{split} x_1 &= 13.3333333.. \\ x_2 &= y = 3.3333333.. \\ \end{split}\]
Ricerca Operativa (9/12)
Il valore della soluzione invece è dato da
\[f(x_1, x_2) = 180x_1 + 200x_2 \approx 3066.666\]
Ricerca Operativa (10/12)
La soluzione è stata ottenuta utilizzando online-optimizer.appspot.com con il seguente programma lineare
var x1 >= 0; var x2 >= 0; maximize z: 180*x1 + 200*x2; subject to c11: 5*x1 + 4*x2 <= 80; subject to c12: 10*x1 + 20*x2 <= 200; subject to c13: x1 >= 0; subject to c14: x2 >= 0; end;
Ricerca Operativa (11/12)
Tramite lo studio della ricerca operativa, chiamata anche programmazione lineare, si è in grado di capire come risolvere problemi della forma e della sostanza appena mostrata.
Ricerca Operativa (12/12)
Tali problemi possono essere usati come modelli matematici di innumerevoli situazioni di ottimizzazione in cui ci si può imbattere nella vita reale.
Questo rende la ricerca operativa una branca fondamentale della matematica applicata.