ASD2 - 06 - Riduzioni II
Date:
Course Site:
Lecturer: Francesco Pasquale
Table of Contents:
In questa lezione abbiamo visto i primi problemi computazionalmente difficile da risolvere, introducendo come le le riduzioni polinomiali possono essere utilizzare per dimostrare la difficoltà di un problema.
Non tutti i problemi purtroppo possono essere risolti in modo efficiente rispetto alle risorse computazionali utilizzate come tempo e/o spazio.
In una precedente lezione avevamo introdotto come poter utilizzare la tecnica della riduzione polinomiale per poter risolvere dei problemi in modo efficiente. In questa lezione mostriamo un secondo utilizzo delle riduzioni polinomiali. In particolare mostriamo come possono essere utilizzate per dimostrare formalmente che un problema \(Q\) è "difficile" tanto quanto un problema \(P\).
Per fare questo l'idea è quella di prendere il problema \(P\) che già so essere "difficile" e trovare una riduzione polinomiale \(f\) da \(P\) a \(Q\), dimostrando quindi che \(P \preceq Q\). Se questo è vero abbiamo che l'eventuale scoperta di un algoritmo polinomiale per \(Q\) mi permetterebbe, tramite la riduzione \(f\), di risolvere anche il problema \(P\): a partire da una istanza \(I\) di \(P\) utilizzo la riduzione \(f\) per trasformarla, in tempo polinomiale, in una istanza \(f(I)\) di \(Q\). Tramite l'algoritmo di \(Q\) poi risolvo \(f(I)\) in \(Q\), e, dal fatto che \(f\) è una riduzione, risolvendo \(f(I)\) in \(Q\) sto anche risolvendo \(I\) in \(P\).
Vediamo quindi alcuni esempi di riduzioni utilizzate per dimostrare la \(\text{NP}\) -completezza di alcuni problemi. Iniziamo assumendo di conoscere che il problema \(\text{SAT}\) è un problema \(\text{NP}\) completo.
Ricordiamo che il problema 3-SAT è definito come la tripla \(\langle I, S(I), \pi(I, S(I)) \rangle\) tale che:
L'insieme delle istanze \(I\) è formato dalle coppie \((f, x)\), dove \(f\) è una formula booleana definita sulle variabili \(X\) in forma congiuntiva normale (CNF) in cui ogni clausola ha \(3\) letterali al massimo, mentre l'insieme \(X = \{x_1, x_2, \ldots, x_n\}\) è l'insieme delle variabili.
L'insieme delle possibili soluzioni \(S(I)\) è dato da tutte le assegnazioni di verità \(a: X \to \{\text{True}, \text{False}\}\) che associano ad ogni variabile in \(X\) un valore vero/falso.
Il predicato che una possibile soluzione deve rispettare per essere una effettiva soluzione è il seguente
\[\pi(I, S(I)) = \,\, \exists a \in S(I): \,\, f(a(X)) \text{ è soddisfatta}\]
Al fine di ridurre il problema SAT al problema 3-SAT dobbiamo trasformare le clausole di SAT in clausole di 3-SAT. Segue quindi qualche esempio di trasformazione
In generale quindi una clausola di SAT della forma \(l_1 \lor l_2 \lor \ldots \lor l_k\) viene trasformata nella seguente clausola 3-SAT
\[\begin{split} (l_1 \lor l_2 \lor y_1) &\land (\neg y_1 \lor l_3 \lor y_2) \\ &\land \ldots \\ &\land (\neg y_{i-2} \lor l_i \lor y_{i-1}) \\ &\land \ldots \\ &\land (\neg y_{k-4} \lor l_{k-2} \lor y_{k-3}) \\ &\land (\neg y_{k-3} \lor l_{k-1} \lor l_k) \\ \end{split}\]
Siamo quindi pronti per definire formalmente la nostra riduzione \(f:I_{\text{SAT}} \to I_{\text{3-SAT}}\) come segue
\[f(g, x) = (g', x')\]
dove \(g'\) è la formula ottenuta da \(g\) sostituendo tutte le clausole di SAT della forma \((l_1 \lor l_2 \lor \ldots \lor l_k)\) con \(k \geq 4\) come abbiamo appena fatto vedere, mentre \(X' := X \cup Y\), con \(Y\) insieme delle variabili introdotte nella procedura di sostituzioni delle clausole descritta prima.
Andiamo adesso a dimostrare che \(f\) è una riduzione polinomiale. Per fare questo dobbiamo dimostrare che
\(f\) richiede un tempo di calcolo polinomiale rispetto alla dimensione dell'input.
\((g, X)\) è una istanza positiva per il problema SAT se e solo se \(f(g, X)\) è una istanza positiva per il problema 3-SAT. In formula,
\[(g, X) \in \text{SAT} \iff f(g, X) \in \text{3-SAT}\]
Notiamo che il primo punto è banale da vedere, in quanto per ogni clasuola di lunghezza \(k\) dell'istanza originale dobbiamo introdurre \(k-3\) variabili extra. Per quanto riguarda il secondo punto invece procediamo dimostrando entrambi i lati dell'equivalenza.
Sia \((g, X) \in \text{SAT}\). Dunque esiste una assegnazione di verità \(\tau: X \to \{\text{True}, \text{False}\}\) tale che \(g(\tau(X))\) è soddisfatta. A partire da tale assegnazione, che soddisfa \(g\), andiamo a costruirne una \(\tau': X' \to \{\text{True}, \text{False}\}\) che soddisfa \(g'\). A tale fine iniziamo nel seguente modo
\[\forall x \in X: \tau'(x) := \tau(x)\]
Ora, dato che \(g(\tau(X))\) è soddisfatta, abbiamo che per ogni clasuola \(c\) di \(g\) esiste un letterale \(l_i\) per cui vale \(\tau(l_i) = \text{True}\). Se la clausola in questione ha meno di \(4\) letterali, allora sarà soddisfatta anche da \(\tau'\) senza ulteriori accorgimenti. Altrimenti, se la clausola in questione ha più di \(4\) letterali, l'idea è quella di localizzare la clausola in \(g'\) che contiene \(l_i\) per poi settare a \(\text{True}\) tutte le variabili \(y_j\) con \(j < i\) e a \(\text{False}\) tutte le variabili \(y_j\) con \(j > i\). Così facendo riesco a soddisffare tutte le clausole introdotte per coprire la clausola \(c\) che è soddisfatta da \(\tau\) tramite il letterale \(l_i\).
Ripetendo questo procedimento per ogni clausola \(c\) della formula originale \(g\) siamo in grado di ottenere una assegnazione di verità \(\tau'\) che soddisfa \(g'\).
\[\tag*{$\checkmark$}\]
Sia \(f(g, X) \in \text{3-SAT}\). Notiamo che se esiste una assegnazione di verità \(\tau'\) che soddisfa \(g'\), allora considerando una catena di clausole introdotte in \(g'\) per rappresentare la clausola \((l_1 \lor l_2 \lor \ldots \lor l_k)\) deve essere il caso che deve esistere almeno un letterale per cui \(\tau'(l_i) = \text{True}\), in quanto non possiamo soddisfare tutte le clasuole giocando con i valori di verità delle variabili introdotte \(y_1, y_2, \ldots y_{k-3}\).
Ma allora possiamo costruire l'assegnazione \(\tau\) che soddisfa \(g'\) semplicemente prendendo
\[\forall x \in X: \tau(x) := \tau'(x)\]
e notando che così facendo \(\tau\) soddisfa \(g\).
\[\tag*{$\checkmark$}\]
Avendo dimostrato entrambi i lati, la riduzione è completata. Possiamo quindi formalmente dire che il problema 3-SAT è difficile tanto quanto il problema SAT.
\[\tag*{$\blacksquare$}\]
Ricordiamo che il Independent Set (IS) ci chiede se, dato un grafo non diretto \(G\) e un intero \(k\), esiste un \(G\) un insieme di almeno \(k\) nodi scollegati tra loro. Formalmente il problema è descritto dalla tripla \(\langle I_{\text{IS}}, S_{\text{IS}}, \pi_{\text{IS}}\rangle\), dove
L'insieme delle istanze \(I_{\text{IS}}\) è formato dalle coppie \((G=(V,E), k)\), dove \(G\) è un grafo non diretto e \(k \in \mathbb{N}\).
L'insieme delle possibili soluzioni \(S_{\text{IS}}(G, k)\) è dato dall'insieme di tutti i possibili sottoinsiemi \(V'\) di \(V\), \(V' \subseteq V\).
Il predicato \(\pi_{\text{IS}}(G, K, S_{\text{IS}}(G, k))\) che una possibile soluzione deve rispettare per essere una effettiva soluzione è il seguente
\[\exists V' \in S_{\text{IS}}(G, k): \,\, |V'| \geq k \,\, \land \,\, \forall u, v \in V': (u, v) \not \in E\]
Osservazione: Notiamo che il problema di ottimizzazione MaximumIndipendentSet è difficile tanto quanto il problema di decisione IS.
Come solitamente avviene nelle riduzioni, come prima cosa dobbiamo capire come trasformare una istanza del problema da cui partiamo, nel nostro caso 3-SAT, in una istanza del problema di arrivo, nel nostro caso IS. Consideriamo quindi la seguente formula di 3-SAT
\[\varphi := (l_1 \lor l_2 \lor l_3) \land (\neg l_2 \lor l_3 \lor l_4) \land (l_2 \lor l_3 \lor \neg l_4)\]
un possibile modo per passare ad un grafo, il grafo \(G_{\varphi}\), è il seguente
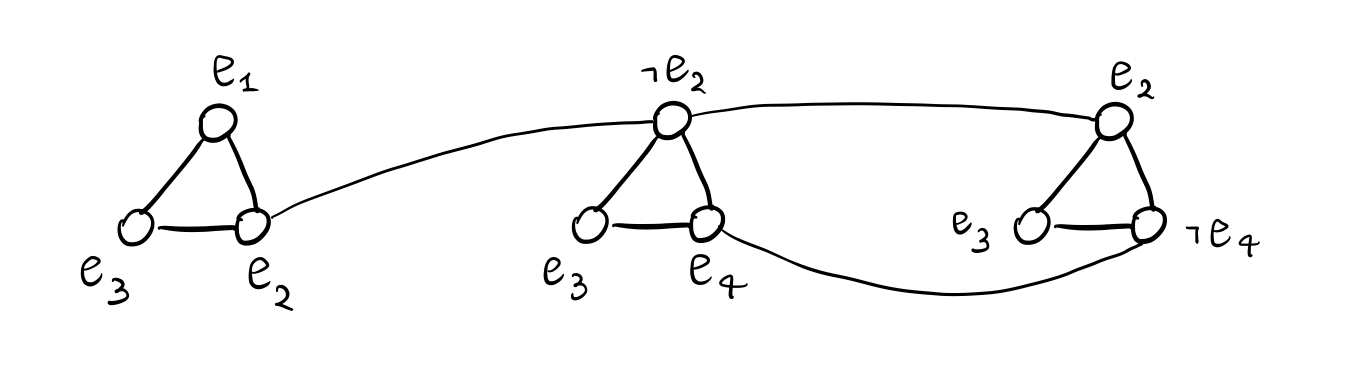
L'idea è che ogni triangolo del grafo rappresenta una particolare clausola della formula \(\varphi\). Con questa costruzione prendere un nodo all'interno di un triangolo significa selezionare quale letterale rendere vero per soddisfare la formula. Infine, per porre il vincolo che se soddisfaciamo una clausola prendendo un letterale \(l\), allora non possiamo soddisfare altre clausole prendendo il letterale \(\neg l\), utilizziamo gli archi che collegano triangoli diversi. Così facendo infatti siamo costretti a scegliere un letterale diverso da \(\neg l\) per soddisfare i rimanenti triangoli.
Siamo ora in grado di definire formalmente la nostra riduzione \(f: I_{\text{3-SAT}} \to I_{\text{IS}}\) come segue
\[f(\varphi, X) := (G_{\varphi}, m)\]
dove \(m\) è il numero di clausole di \(\varphi\) e \(G_{\varphi} = (V, E)\) è il grafo costruito a partire dalla formula
\[\varphi = (l_1^1 \lor \land \lor l_{h_1}^1) \land (l_1^2 \lor \ldots \lor l_{h_2}^2) \land \ldots \land (l_1^m \lor \ldots \lor l_{h_m}^m)\]
con \(l_j^i\) letterale e \(h_i \in \{1, 2, 3\}\) per \(i = 1,...,m\), nel seguente modo
L'insieme dei vertici \(V\) è dato da dalle istanze di tutti i letterali
\[V := \{l_k^i \,\,|\,\, i=1,...,m, \,\, k = 1,...,h_i\}\]
L'insieme degli archi \(E\) invece è ottenuto mettendo gli archi che uniscono i letterali nella stessa clausola, e gli archi che uniscono i letterali con i propri negati in clausole diverse.
\[\begin{split} E := \{(l_k^i, l_j^i) \,\,&|\,\, i = 1,...,m \,\,\, k \,\,,\,\, j = 1, ..., h_i\} \,\,\bigcup \\ & \{(l_k^{i_1}, l_j^{i_2} \,\,|\,\, i_1,i_2 = 1,...,m \,\,,\,\, l_k^{i_1} = \neg l_j^{i_2}\} \end{split}\]
Si può subito vedere che la costruzione di \(G_{\varphi}\) richiede tempo polinomiale in \(|\varphi|\). Inoltre è possibile far vedere che se \(m\) è il numero di clausole, allora esisterà un insieme indipendente \(V'\) in \(G_{\varphi}\) con \(|V'| \geq m\) se e solo se la formula \(\varphi\) è soddisfacibile.
Se \((\varphi, X) \in \text{3-SAT}\), allora esiste una assegnazione di verità \(\tau\) che soddisfa \(\varphi\).
Per ogni clausola in \(\varphi\), ovvero per ogni triangolo in \(G_{\varphi}\), andiamo a prendere solamente un letterale che viene impostato a \(\text{True}\) dall'assegnazione \(\tau\) e lo inseriamo in \(V'\).
È possibile vedere che \(V'\) è un indipendent set con \(|V'| = m \geq m\), e quindi \(f(\varphi, X)\) risolve l'istanza del problema \(\text{IS}\).
\[\tag*{$\checkmark$}\]
Viceversa, se \(f(\varphi, X) \in \text{IS}\), allora esiste un indipendent set \(V' \subseteq V\) con \(|V'| \geq m\). L'idea è quella di costruire una assegnazione di verità \(\tau\) nel seguente modo
\[\forall x \in V: \,\,\,\, \tau(x) = \begin{cases} \text{True} \,\,\,&,\,\,\, x \in V' \\ \text{False} \,\,\,&,\,\,\, \neg x \in V' \\ \end{cases}\]
Notiamo che \(V'\) contiene \(m\) elementi, e quindi l'assegnazione \(\tau\) definita rende vera ogni clausola in cui è presente almeno un letterale contenuto in \(V'\). Dato che \(V'\) è un insieme indipendente, allora deve necessariamente contenere letterali presi da \(m\) diverse clausole, e visto che non può essere che \(x \in V'\) e \(\neg x \in V'\) ne segue che \(\tau\) soddisfa \(m\) clausole diverse, e quindi soddisfa la formula \(\varphi\).
\[\tag*{$\checkmark$}\]
Avendo dimostrato entrambi i lati, la riduzione è completata. Possiamo quindi formalmente dire che il problema IS è difficile tanto quanto il problema 3-SAT.
\[\tag*{$\blacksquare$}\]
Ricordiamo che il problema Vertex Cover (VC) è definito dalla tripla \(\langle I_{\text{VC}}, S_{\text{VC}}, \pi_{\text{VC}} \rangle\) dove,
L'insieme delle istanze \(I_{\text{VC}}\) è formato da coppie \((G, k)\) in cui \(G\) è un grafo non diretto e \(k \in \mathbb{N}\).
L'insieme delle possibili soluzioni è dato da tutti i sottoinsiemi di \(V\)
\[S_{\text{VC}}(G, k) := \{V' \subseteq V\}\]
Il predicato \(\pi_{\text{VC}}((G, k), S_{\text{VC}}(G, k))\) che una possibile soluzione deve rispettare per essere considera una soluzione effettiva è il seguente
\[\exists V' \in S_{\text{VC}}(G, k): |V'| \leq k \land \forall (u, v) \in E: \Big[ u \in V' \lor v \in V' \Big]\]
Per costruire la riduzione \(f: I_{\text{IS}} \to I_{\text{VC}}\) l'idea è quella di utilizzare il seguente fatto
\(V'\) è un independent set di \(G\) se e solo se \(V \setminus V'\) è un vertex cover di \(G\).
Infatti,
\[\begin{split} V' \subseteq V \text{ è un indipendent set} &\iff \forall (u, v) \in E: \,\,\, \neg \Big(u \in V' \land v \in V' \Big) \\ &\iff u \not \in V' \lor v \not \in V'\\ &\iff u \in V \setminus V' \lor v \in V \setminus V' \\ &\iff V \setminus V' \text{ è un vertex cover} \end{split}\]
Possiamo quindi costruire formalmente la nostra riduzione \(f: I_{\text{IS}} \to I_{\text{VC}}\) nel seguente modo
\[f(G, k) = f(G, n-k)\]
con \(n = |V|\).
Infine, dimostriamo che \((G, k) \in \text{IS} \iff f(G, k) \in \text{VC}\):
\((\Rightarrow)\): Sia \(V' \subseteq V\) un independent set di \(G\), con \(|V'| \geq k\). Per la proprietà discussa prima sappiamo che \(V \setminus V'\) è un vertex cover per \(G\). Infine, dato che \(|V'| \geq k\), abbiamo che \(|V \setminus V'| \leq n-k\).
\[\tag*{$\checkmark$}\]
\((\Leftarrow)\): Se \(V' \subseteq V\) è un vertex cover con \(|V'| \leq n-k\), allora \(V \setminus V'\) è un IS con \(|V \setminus V'| \geq n - (n - k) = k\) nodi.
\[\tag*{$\checkmark$}\]
Avendo dimostrato entrambi i lati, la riduzione è completata. Possiamo quindi formalmente dire che il problema VC è difficile tanto quanto il problema IS.
\[\tag*{$\blacksquare$}\]
La riduzione da VC a IS, \(f: I_{\text{VC}} \to I_{\text{IS}}\) è uguale da quella da IS a VC, ed in particolare è definita come segue
\[f(G, k) = (G, n-k)\]
si può far vedere, in modo analogo a quanto visto in precedenza, che
\[(G, k) \in \text{VC} \iff f(G, k) \in \text{IS}\]
\[\tag*{$\blacksquare$}\]
Il problema Clique (CL) ci chiede se, dato un grafo non diretto \(G\) e un intero \(k\), esiste un sottoinsieme di almeno \(k\) nodi che siano tutti collegati tra loro, formando una cricca. Formalmente è definito dalla seguente tripla \(\langle I_{\text{CL}}, S_{\text{CL}}, \pi_{\text{CL}} \rangle\), dove
L'insieme delle istanze \(I_{\text{CL}}\) è formato da coppie \((G, k)\) dove \(G\) è un grafo non diretto e \(k \in \mathbb{N}\) è un intero positivo.
L'insieme delle possibili soluzioni è dato da tutti i sottoinsiemi di \(V\)
\[S_{\text{CL}}(G, k) = \{V' \subseteq V\}\]
Il predicato \(\pi_{\text{CL}}(G, k, S_{\text{CL}}(G, k))\) che una possibile soluzione deve rispettare per poter essere considerata una effettiva soluzione è il seguente
\[\exists V' \in S_{\text{CL}}(G, k): |V'| \geq k \,\, \land \,\, \forall u, v \in V': (u, v) \in E\]
Definiamo quindi la nostra riduzione \(f: I_{\text{IS}} \to I_{\text{CL}}\)
\[f(G, k) := (\overline{G}, k)\]
dove il grafo \(\overline{G} = (\overline{V}, \overline{E})\) è costruito a partire dal grafo \(G = (V, E)\) nel seguente modo
\(\overline{V} := V\)
\(\forall u, v \in \overline{V}: \,\, (u, v) \in \overline{E} \iff (u, v) \not \in E\)
Si può subito osservare che il calcolo di \(f\) richiede un costo temporale di \(O(|V| + |V|^2|E|)\), che è quindi polinomiale rispetto alla dimensione dell'istanza.
Per finire, dobbiamo dimostrare che \((G, k) \in \text{IS} \iff f(G, k) \in \text{CL}\).
\((\Rightarrow)\): Sia \((G, k) \in \text{IS}\). Allora esiste un sottoinsieme \(V'\) tale che \(|V'| \geq k\) e per ogni coppia \(u, v \in V'\) si ha \((u, v) \not \in E\). Quindi, per costruzione, in \(\overline{G}\) si ha che per ogni coppia \(u, v \in V'\): \((u, v) \in \overline{E}\). Ovvero \(V'\) è una clinque di cardinalità \(\geq k\). Quindi \(f(G, k) \in \text{CL}\).
\[\tag*{$\checkmark$}\]
\((\Leftarrow)\): Sia \(f(G, k) \in \text{CL}\), allora \(\exists V' \subseteq \overline{V}\) tale che \(|V'| \geq k\) e per ogni coppia \(u, v \in \overline{V}\) si ha \((u, v) \in \overline{E}\). Nuovamente, abbiamo che utilizzando lo stesso insieme di nodi \(V'\) ma in \(G\) troviamo che per ogni coppia \(u, v \in V: (u, v) \not \in E\). Quindi \((G, k) \in \text{IS}\).
\[\tag*{$\checkmark$}\]
Avendo dimostrato entrambi i lati, la riduzione è completata. Possiamo quindi formalmente dire che il problema CLIQUE è difficile tanto quanto il problema IS.
\[\tag*{$\blacksquare$}\]
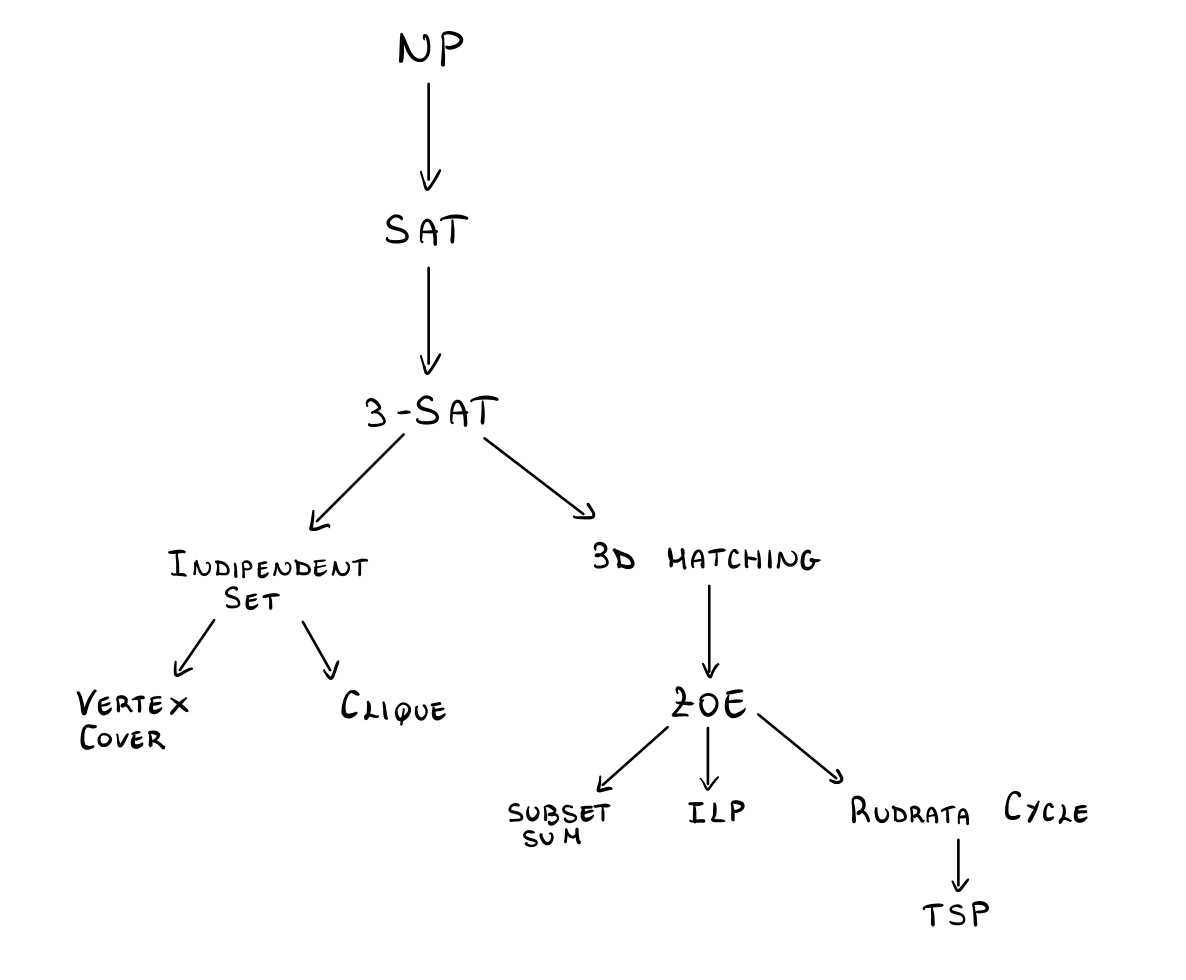
Segue una mappa che mostra l'ordine in cui è possibile dimostrare facilmente la difficoltà dei problemi.