ADRC - 02 - Broadcast I

1 Lecture Info

Data: [2018-10-11 gio] + [2018-10-15 lun]

Capitolo del libro: 2 - Basic Problems and Protocols

In questa lezione abbiamo analizzato il problema del broadcast, definendo i nostri primi protocolli distribuiti. La lezione è stata terminata dimostrando un lower bound per la message complexity del problema, facendo vedere che il protocollo da noi trovato è ottimale in termini di messaggi inviati.

2 Problema del Broadcast

Il problema del broadcast consiste nella condivisione di una informazione, inizialmente conosciuta da un solo nodo della rete, a tutti i nodi della rete. Indichiamo con $I$ l'informazione da condividere. Formalmente il problema del broadcast è descritto dalla seguente tripla $B = \langle B_{init}, B_{final}, R\rangle$, con

$B_{init}(t) \equiv \exists x \in \xi: \Big[ \text{value}_t(x) = I \,\,\, \land \,\,\, \forall y \neq x: \text{value}_t(y) = \emptyset \Big]$

$B_{final}(t) \equiv \forall x \in \xi: \Big[ \text{value}_t(x) = I \Big]$

$R = \begin{cases} \text{Total Reliability (TR)} \\ \text{Bidirectional Link (BL)} \\ \text{Connectivity (CN)} \end{cases}$

Notiamo che una restrizione implicita nel problema che non viene esplicitata in $R$ è la $\text{Unique Initiator (UI)}$, che ci dice che inizialmente c'è un solo nodo attivo. Tale nodo nel nostro caso è proprio l'unico nodo che possiede l'informazione che vogliamo condividere con il resto della rete.

3 Risolvere il Broadcast

Un possibile approccio per risolvere il broadcast consiste nell'applicazione della seguente regola greedy:

\[\begin{split} &\text{Appena una entità viene a conoscenza della nuova informazione } I \text{, } \\ &\text{l'informazione } I \text{ viene condivisa a tutti i suoi vicini.} \end{split}\]

Tale regola può essere implementata nei seguenti due modi diversi.

3.1 Protocollo 1

In questo primo protocollo abbiamo i seguenti stati

$S := \{\text{Initiator}, \text{Idle}\}$

$S_{init} := S$

le azioni invece sono descritte come segue

Notiamo che per come è stato definito, il protocollo non termina mai. Inoltre vengono inviati un totale di

\[\sum_{x \in V} |N(x)| = 2 \cdot |E| = 2m\]

messaggi per condividere l'informazione con tutta la rete. Questa complessità non è ottimale, in quanto quando un nodo $x \in \xi$ riceve l'informazione $(I)$ da un nodo $y \in \xi$, non c'è bisogno da parte del nodo $x$ di inviare nuovamente $(I)$ al nodo $y$. Possiamo quindi migliorare il protocollo appena descritto per ottenere un nuovo protocollo.

3.2 Protocollo Flooding

In questo protocollo, a differenza di quello di prima, abbiamo un ulteriore stato che indica la terminazione delle attività dei nodi. In totale troviamo quindi i seguenti stati:

$S := \{\text{Initiator}, \text{Idle}, \text{done}\}$

$S_{init} := \{\text{Initiator}, \text{Idle}\}$

$S_{term} := \{\text{Done}\}$

Le azioni invece sono descritte come segue

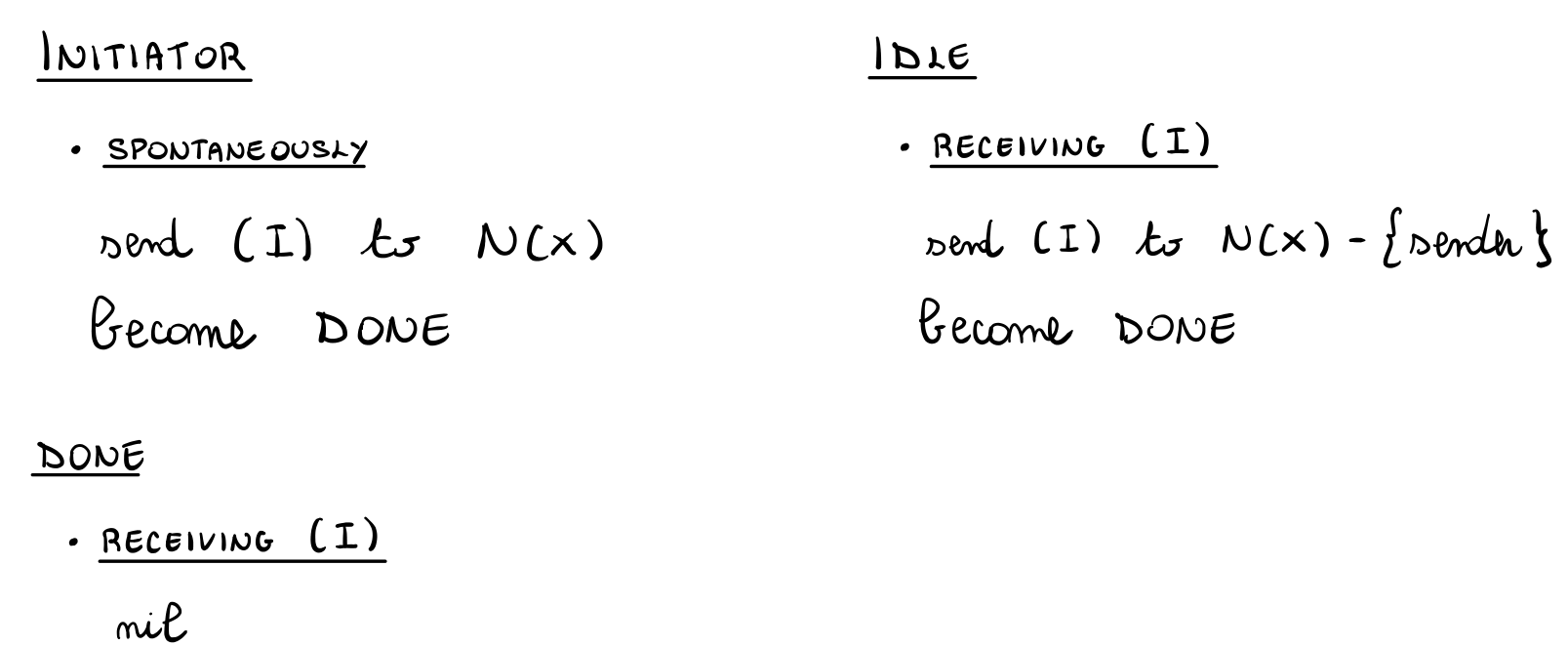
andiamo adesso ad argomentare la correttezza e la complessità del protocollo appena descritto.

3.2.1 Correttezza

Sia $\overrightarrow{G} = (V, \overrightarrow{E})$ la rete del sistema, e supponiamo che $\overrightarrow{G}$ rispetti le restrizioni in $R$. Per dimostrare la correttezza dell'algoritmo vogliamo dimostrare che

\[\exists t \in \mathbb{N}: \,\,\, Correct(t) \,\,\, \land \,\,\, Terminate(t)\]

nel caso specifico del problema del broadcast troviamo

\[\exists t \in \mathbb{N}: \forall x \in \xi: \,\, \Big[ \text{value}_t(x) = I \,\,\, \land \,\,\, status_t(x) = \text{Done} \Big]\]

in altre parole vogliamo dimostrare che esiste un tempo finito $t$ in cui tutti i nodi posseggono l'informazione e si trovano nello stato $Done$.

Dimostrazione: Sia $s \in V$ l'initiator. Procediamo per induzione sulla distanza di un nodo $x \in V$ da $s$. Come ipotesi induttiva assumiamo quindi che tutti i nodi a distanza $d$ da $s$ ricevono in un tempo finito l'informazione $I$ e si spostano nello stato $\text{Done}$. Notiamo che il valore di $d$ può variare nel seguente insieme $d \in \{0, 1, \ldots, diam(G)\}$

Caso Base $(d = 0)$:

L'unico nodo a distanza $0$ da $s$ è $s$ stesso, che ha già l'informazione $(I)$ al tempo $t=0$.

\[\tag*{$\checkmark$}\]
Passo Induttivo $(d > 0)$:

Assumiamo l'ipotesi induttiva per il caso $d$ e dimostriamo che vale anche per il caso $d+1$. A tale fine suddividiamo i nodi del grafo in base alla loro distanza dal nodo $s$ per ottenere

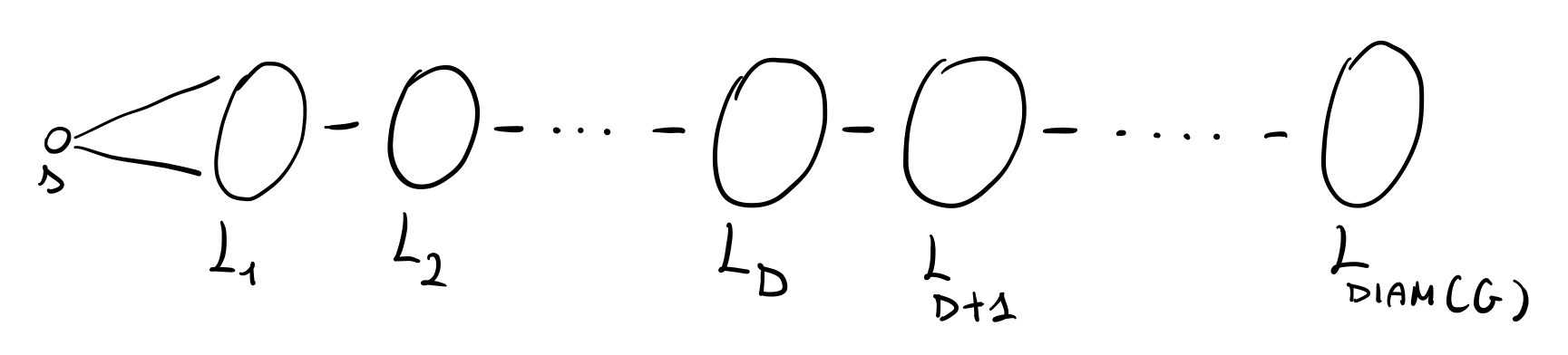
dove l'insieme $L_i$ contiene i nodi del grafo che si trovano a distanza $i$ da $s$.

Dall'ipotesi induttiva segue che tutti i nodi in $L_d$ sono informati al tempo $t \in \mathbb{N}$. Sia quindi $x \in V$ un nodo in $L_{d+1}$. Per costruzione $x$ è adiacente ad un nodo $y \in L_d$. Abbiamo quindi i seguenti due casi:
- Se $y$ è informato da $x$, allora $x$ è già stato informato al tempo $t$, e quindi si trova nello stato $\text{Done}$.
- Se $y$ non è informato da $x$, allora dopo essere informato, $y$ informerà $x$, facendolo passare allo stato $\text{Done}$.
In entrambi i casi esiste un tempo finito $t^{'}$ in cui tutti i nodi in $L_{d+1}$ vengono informati.

\[\tag*{$\checkmark$}\]

Avendo dimostrato entrambi i casi, la dimostrazione è conclusa.

\[\tag*{$\blacksquare$}\]

3.2.2 Complessità

Per quanto riguarda la message complexity, introdotta nella precedente lezione, andiamo ad effettuare una analisi per nodo, ovvero vediamo quanti messaggi invia ciascun nodo. Notiamo che abbiamo due casi, a seconda del nodo preso in considerazione:

Per il nodo sorgente, ovvero il nodo initiator $s$, paghiamo esattamente il grado del nodo initiator, che è pari a $|N(s)|$.
Per i nodi restanti $x\neq s$ invece paghiamo esattamente $|N(x)|-1$ in quanto inviamo l'informazione $(I)$ a tutti i nodi tranne al nodo che ci ha informato.

Mettendo tutto insieme troviamo la seguente complessità

\[\begin{split} \phantom{}| N(s) | + \sum\limits_{v \in V: v \neq s} |N(v)| - 1 &= -(n-1) + \sum\limits_{v \in V} |N(v)| \\ &= -(n-1) + 2m \\ &= 2m -n + 1 \\ &= O(2m) \\ \end{split}\]

Effettuando una analisi per arco invece troviamo che in ogni arco possono passare al massimo $2$ messaggi. In totale troviamo quindi sempre una message complexity di $O(2m)$.

Per quanto riguarda la ideal time complexity invece, se assumiamo di lavorare in un sistema sincrono in cui tutti i messaggi spediti al tempo $t-1$ vengono ricevuti al tempo $t$, abbiamo un ideal time pari a $diam(G)$, in quanto all'istante di tempo $t$ l'informazione $I$ è stata sicuramente condivisa a tutti i nodi a distanza $t$ dalla sorgente.

4 Lower Bound per il Broadcast

Abbiamo dimostrato che il protocollo flooding risolve il broadcast con una message complexity di $O(m)$. Poniamoci adesso il problema di capire se questo risultato è ottimale. In altre parole, possiamo fare di meglio? Esiste un protocollo che risolve il broadcast inviando meno di $m$ messaggi?

Notiamo che $n-1$ è un lower bound banale alla message complexity per il broadcast: ogni nodo infatti deve ricevere l'informazione da un altro nodo, e quindi devono almeno essere inviati $n-1$ messaggi. Troviamo quindi un gap tra $n-1$ e $m = O(n^2)$ che ci potrebbe portare a pensare che, forse, potremmo fare di meglio di $m$.

Detto questo, lavorando in una topologia di rete generale che rispetta le restrizioni in $R$ è possibile dimostrare che non esiste un protocollo migliore del flooding per il broadcast. Vale infatti il seguente risultato

Teorema: Sotto le restrizioni $R = \{\text{TR}, \text{CN}, \text{BL}, \text{UI}\}$, tutti i protocolli che risolvono il broadcast richiedono, nel caso peggiore, $m$ messaggi.

La dimostrazione che segue utilizza il fatto che un protocollo, per essere corretto, deve funzionare in qualsiasi ambiente di lavoro. L'idea è quindi quella di creare due ambienti diversi per far vedere che in uno di questi due ambienti un protocollo che invia meno di $m$ messaggi non può funzionare correttamente.

Dimostrazione: Per assurdo, sia $P$ un protocollo che risolve il broadcast utilizzando meno di $m$ messaggi e sia $G=(V,E)$ la rete di un sistema distribuito generico.

Eseguendo il protocollo $P$ su $G$, troviamo che in almeno un arco $e = (x, y) \in E$ non passa nessun messaggio. Denotiamo con $E$ questa particolare esecuzione del protocollo.

Costruiamo ora la rete $G^{'} := (V^{'}, E^{'})$ ottenuta da $G$ nel seguente modo

$V^{'} := V \cup \{z\}$ tale che $\,\,\, z \not \in V$
$E^{'} := E \setminus \{(x, y)\} \cup \{(x, z), (y, z)\}$

Notiamo che l'esecuzione $E$ del protocolo $P$ sulla rete $G'$ non informa il nodo $z$: infatti il nodo $z$ può essere informato solo da $x$ o da $y$, ma nell'esecuzione $E$ i nodi $x$ e $y$ non inviano nessun messaggio negli archi $(x, z)$ e $(y, z)$, in quanto nella rete $G$ non passa nessun messaggio nell'arco $(x, y)$.

Graficamente troviamo la seguente situazione

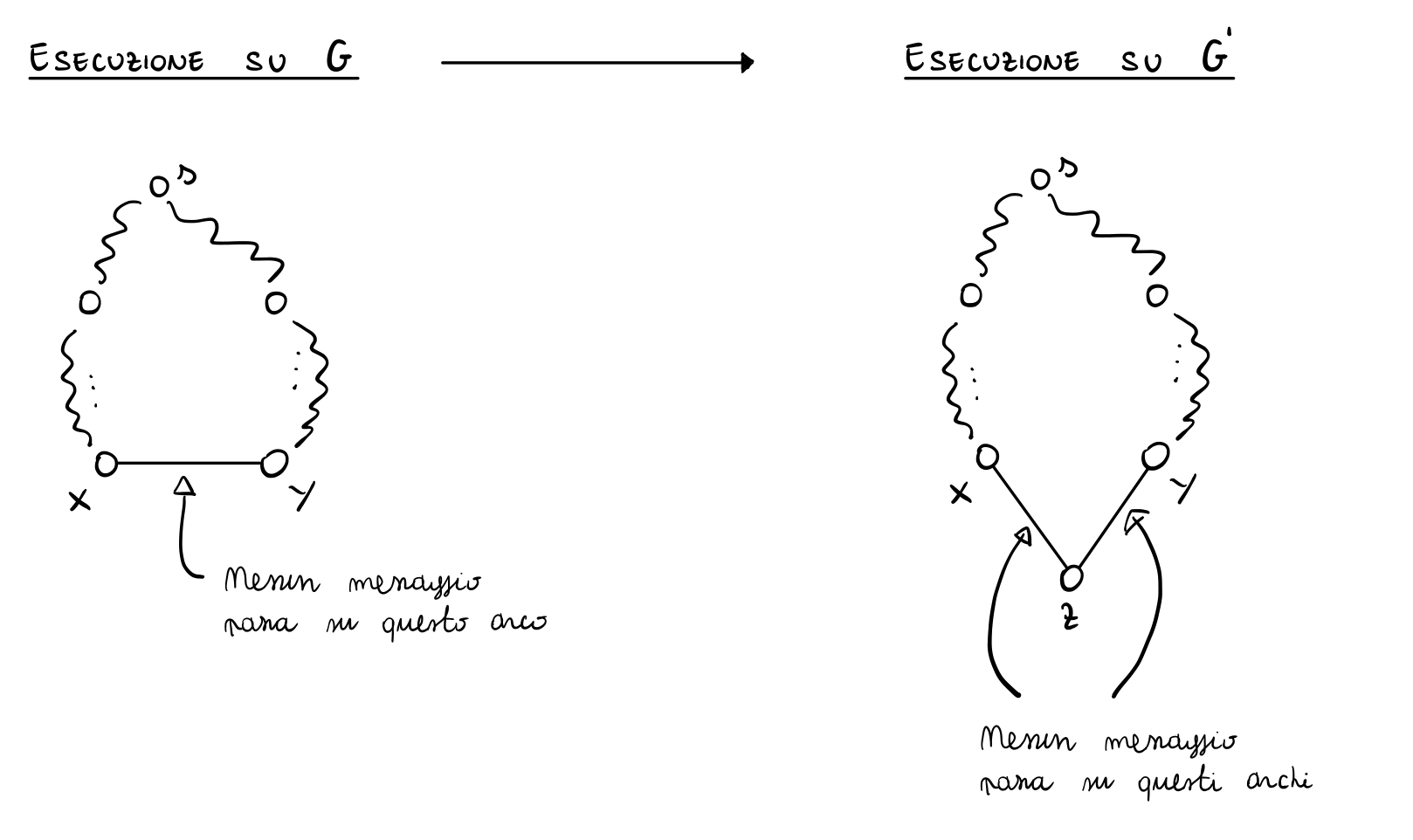
Da questo segue che il protocollo $P$ non risolve correttamente il problema del broadcast, e quindi non può esistere un protocollo che risolve il broadcast utilizzando meno di $m$ messaggi.

\[\tag*{$\Huge\unicode{x21af}$.}\]