ADRC - 03 - Broadcast II

1 Lecture Info

Data: [2018-10-18 gio]

Capitolo del libro: 2 - Basic Problems and Protocols

In questa lezione abbiamo visto come il lower bound di $m$ per il problema del broadcast dimostrato nella scorsa lezione può essere migliorato se lavoriamo su reti con particolari topologie. In particolare abbiamo introdotto la struttura ad hypercube e abbiamo analizziamo il protocollo $\text{hyperflood}$ che ci permette di risolvere il broadcast nell'hypercube in un tempo $O(n \cdot \log n)$.

2 Struttura ad Hypercube

La struttura ad hypercube rappresenta una famiglia di grafi infiniti. La costruzione di uno specifico hypercube può essere effettuata in modo ricorsivo rispetto al diametro $d$ della rete. Per ogni valore di $d$ abbiamo infatti un diverso hypercube. Prima di definire in modo generale come è strutturato un hypercube, andiamo a vedere la costruzione dei più semplici hypercubes, al variare del diametro $d$:

$d = 1$

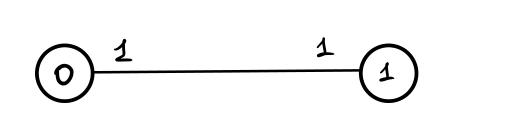
$d = 2$:
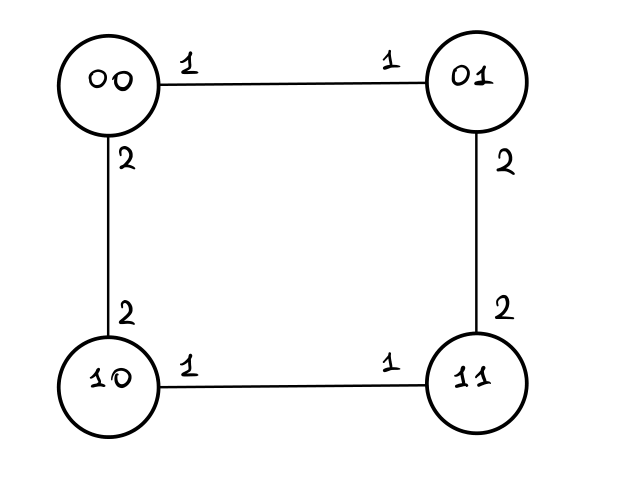
$d = 3$:

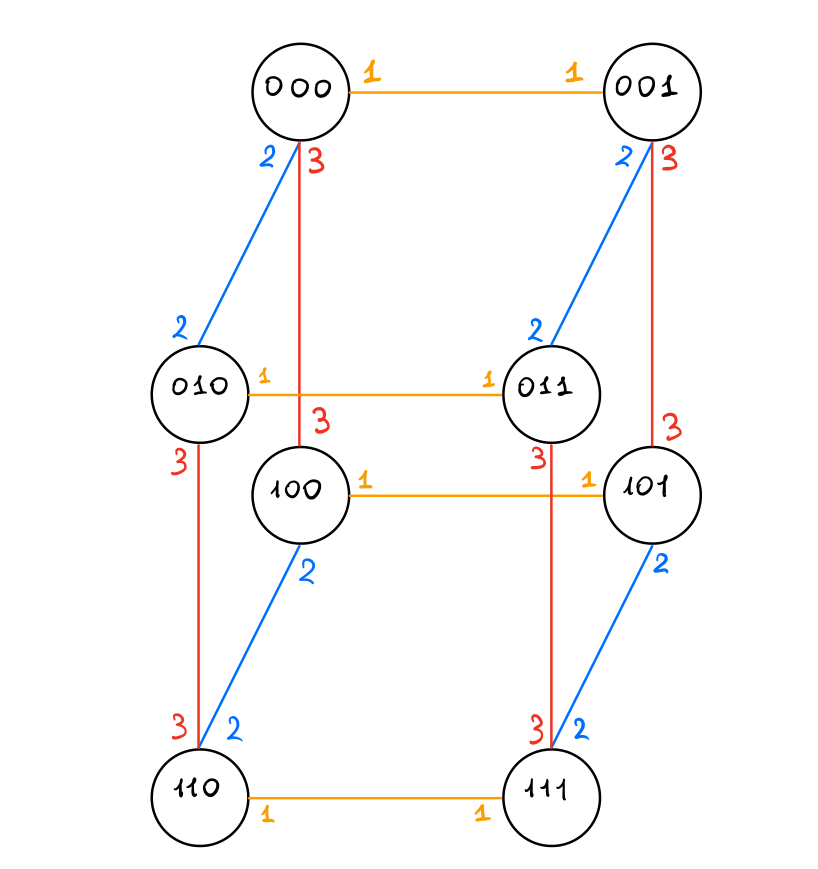
Come possiamo vedere dagli esempi appena mostrati, un hypercube di dimensione $d$ $H_d=(V,E)$ è caratterizzato dal fatto che sia i nodi che gli archi sono etichettati. I nodi sono etichettati da stringhe di bits $(0, 1)$ di lunghezza $d$, mentre gli archi sono etichettati con numeri interi tra $1$ e $d$. Se l'arco $(x, y)$ è etichettato con $i \in \{1, ..., d\}$, allora per passare dell'etichetta del nodo $x$ a quella del nodo $y$ bisogna cambiare il valore dell' $i$ -esimo bit, facendolo passare da $0$ a $1$ e viceversa da $1$ a $0$.

Il valore del diametro $d$ determina varie cose rispetto alla struttura del relativo hypercube $H_d$. Tra queste troviamo

La lunghezza delle etichette dei nodi, che è $d$.
Il grado di ogni nodo, che è $d$.
Il diametro del grafo, che è $d$.
Il valore delle etichette degli archi, che è al massimo $d$.
Il numero dei nodi, che è $2^d$.

Tutte queste caratteristiche, e in particolare il fatto che il grado di ogni nodo e il diametro della rete sono entrambi logaritmici rispetto al numero di nodi, rendono l'hypercube una struttura molto efficiente e versatile per un sistema distirbuito. Andiamo adesso a vedere come poter risolvere il problema del broadcast in reti che seguono topologie ad hypercube.

3 Broadcast su Hypercube

Andando ad applicare il protocollo di flooding discusso nella precedente lezione troviamo i seguenti risultati rispetto alla message complexity e alla ideal time complexity.

$Msg(\text{flooding}/\text{hypercube}) = O(m) = O(n \cdot \log n)$
$Time(\text{flooding}/\text{hypercube}) = O(diam(G)) = O(\log n)$

Dato che avevamo discusso del lower bound banale di $n-1$, troviamo il seguente gap

\[n - 1 \leq \text{ ? } \leq n \cdot \log n\]

in altre parole, siamo interessati a sapere se esiste un protocollo distribuito più specifico per la struttura ad hypercube che permette di ottenere un risultato migliore di $n \cdot \log n$. Per cercare di rispondere a questa risposta introduciamo quindi un nuovo protocollo distribuito.

3.1 Hyperflood

Assumendo che i nodi siano a conoscenza della topologia ad hypercube della rete, possiamo utilizzare il seguente protocollo distribuito, che prende il nome di hyperflood:

L'initiator invia l'informazione $I$ a tutti i suoi vicini;
Se un nodo $v$ riceve $I$ da un arco con etichetta $l$, allora $v$ invia $I$ a tutti e soli gli archi con etichetta $l^{'}$ tale che $l^{'} \leq l$.

Andiamo adesso ad argomentare la correttezza e la complessità del protocollo appena descritto.

3.1.1 Correttezza

Siamo interessati a far vedere che l'hyperflood riesce a risolvere il problema del broadcast su ogni rete ad hypercube. Per fare questo dobbiamo far vedere che il sottografo $G' = (V, E')$ ottenuto considerando solamente gli archi di $G$ che vengono utilizzati dal protocollo hyperflood è connesso. In questo modo infatti facciamo vedere che ogni nodo ha ricevuto l'informazione $I$ da qualche altro nodo. A tale fine dimostriamo il seguente lemma.

Lemma: Per ogni coppia di nodi $x$ e $y$ in un hypercube $H_k$ di dimensione $k$, esiste un cammino che va da $x$ a $y$ e tale che la sequenza di etichette negli archi del cammino è una sequenza decrescente.

Dimostrazione: Siano $x$ e $y$ due nodi distinti, $x \neq y$ in un hypercube $H_k$ di dimensione $k$. Allora, se consideriamo le loro etichette

$x = \langle x_{k-1}, x_{k-2}, \ldots, x_1, x_0 \rangle$
$y = \langle y_{k-1}, y_{k-2}, \ldots, y_1, y_0 \rangle$

abbiamo che esiste almeno una posizione $i$ in cui $x_i \neq y_i$. Siano $j_1, j_2, \ldots, j_t$ le posizioni in cui le due etichette differiscono, con $t \geq 1$ e $j_i > j_{i+1}$.

Consideriamo adesso la successione di nodi $v_0, v_1, \ldots, v_t$, in cui $v_0 := x$ e il label del nodo $v_i$ è uguale a quello del nodo $v_{i+1}$ tranne per il bit in posizione $j_{i+1}$ per $i = 0, ..., t-1$. Per come abbiamo definito la struttura ad hypercube segue che c'è un arco $(v_i, v_{i+1})$ etichettato con $j_{i+1}$ per ogni $i=0,...,t-1$. Ma allora segue che $v_t = y$. Abbiamo quindi trovato un percorso da $x$ a $y$ con una sequenza decrescente di etichette negli archi.

\[\tag*{$\blacksquare$}\]

Notiamo che dal lemma appena dimostrato segue che l'hyperflood informa tutti i nodi, in quanto a partire da un qualsiasi initiator $x \in V$ che inizialmente conosce $I$, $x$ è in grado di raggiungere qualsiasi nodo $y$ facendo passare $I$ solamente nei cammini caratterizzati da etichette decrescenti negli archi.

3.1.2 Complessità

Dalla discussione precedente abbiamo visto che l'hyperflood informa tutti i nodi utilizzando almeno $n-1$ messaggi. Andiamo ora ad argomentare che l'hyperflood utilizza esattamente $n-1$ messaggi.

Per ottenere questo risultato ci basta dimostrare che il sottografo ottenuto dall'esecuzione del protocollo non può avere cicli. Supponiamo quindi per assurdo che il sottografo in considerazione contiene il seguente ciclo

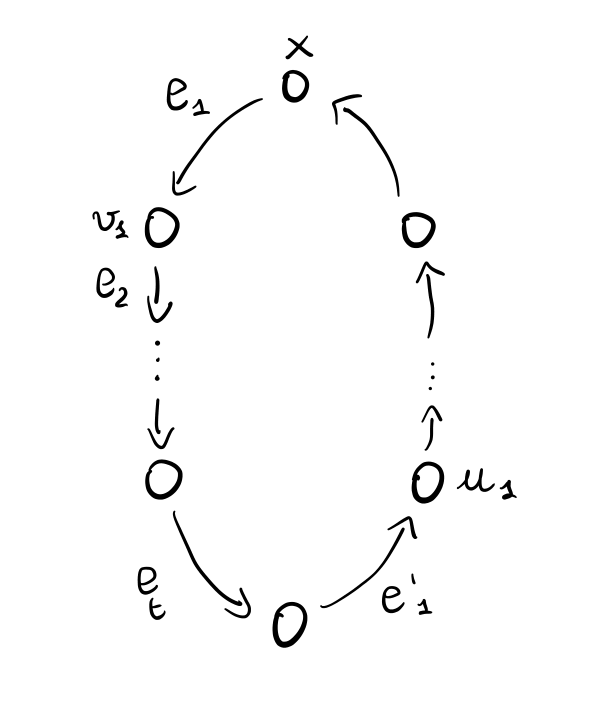
notiamo che la presenza di qualsiasi ciclo implica che un nodo ha inviato l'informazione $I$ ad un arco la cui etichetta era più alta dell'etichetta dell'arco da cui aveva ricevuto l'informazione. Ma questo, per come è stato definito il protocollo, non può succedere.

\[\tag*{$\Huge\unicode{x21af}$}\]

Dunque l'hyperflood ha una message complexity ottimale di $n-1$ su topologie ad hypercube.

4 Overview Broadcast

Andiamo adesso a riassumere i risultati ottenuti per il problema del broadcast.