ADRC - 04 - Wake Up
1 Lecture Info
Data:
Capitolo del libro: 2 - Basic Problems and Protocols
In questa lezione abbiamo trattato il problema del Wake-Up, un problema simile al problema del Broadcast affrontato nelle precedenti lezioni.
2 Problema del Wake Up
Il problema del Wake-Up consite nel partire da una configurazione iniziale in cui abbiamo un sottoinsieme di nodi \(W \subseteq V\) initiators che si trovano nello stato AWAKE e il restante dei nodi \(V \setminus W\) nello stato ASLEEP, e arrivare alla configurazione finale in cui tutti i nodi sono AWAKE.
Formalmente abbiamo quindi la tripla \(P = \langle P_{init}, P_{final}, R \rangle\), in cui:
\(P_{init}(t) \equiv \exists W \subseteq V: W \neq \emptyset \,\,\, \land \,\,\, \forall x \in V: status_t(x) = \begin{cases} \text{awake} \,\,&,\,\, x \in W \\ \text{asleep} \,\,&,\,\, x \in V \setminus W \\ \end{cases}\)
\(P_{final}(t) \equiv \forall x \in V: status_t(x) = \text{awake}\)
\(R = \begin{cases} \text{Total Reliability (TR)} \\ \text{Bidirectional Link (BL)} \\ \text{Connectivity (CN)} \end{cases}\)
3 Protocollo WFLOOD
Per risolvere il problema del Wake-Up possiamo definire il seguente protocollo, che prende il nome di WFLOOD.
Per quanto riguarda gli stati, troviamo la seguente situazione
\(S = \{\text{awake}, \text{asleep}\}\)
\(S_{init} = \{\text{awake}, \text{asleep}\}\)
\(S_{term} = \{\text{awake}\}\)
Per quanto riguarda le azioni dei nodi invece, troviamo la seguente situazione
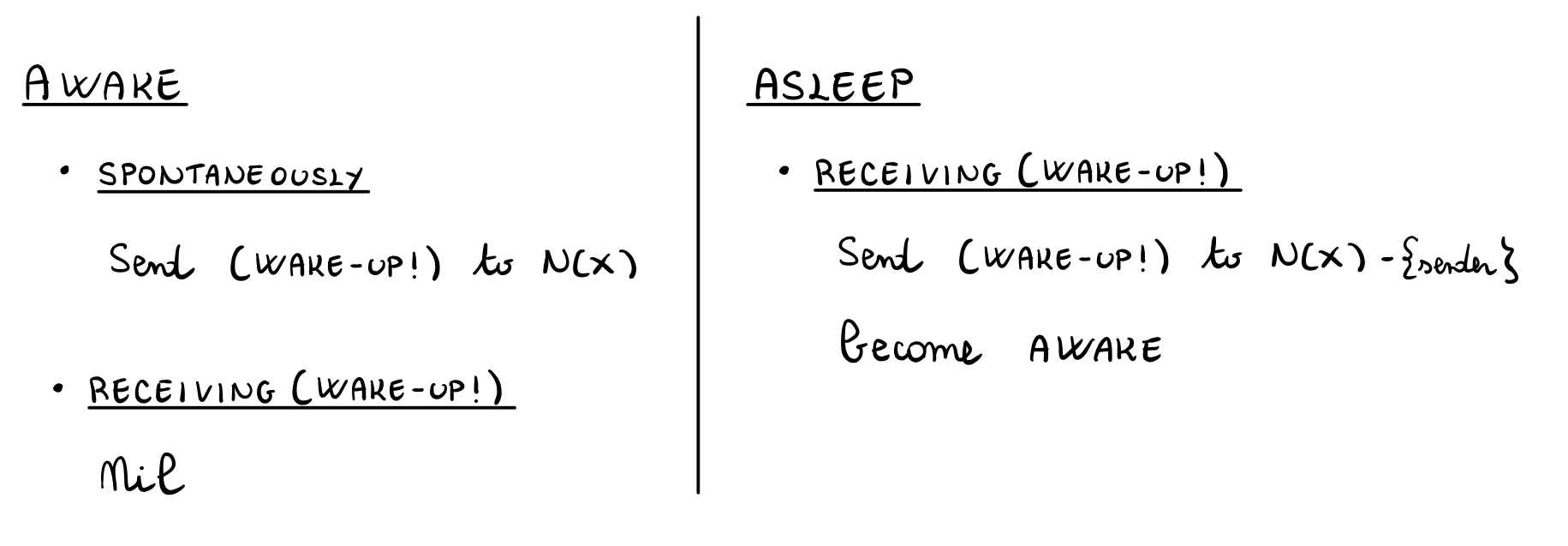
Notiamo che il protocollo WFLOOD è estremamente simile al protocollo FLOODING discusso in una lezione precedente. Questo segue dalla seguente osservazione
\[\text{Broadcast} \iff \text{Wake-Up con un solo nodo awake}\]
dunque il broadcast è un caso speciale del problema più generale del wake-up. Detto in altri termini, possiamo vedere il wake-up come un broadcast in cui però ci possono essere più nodi che al tempo \(t=0\) posseggono l'informazione \(I\) da condividere la restante rete.
Andiamo adesso ad argomentare correttezza e complessità del protocollo appena descritto.
3.1 Correttezza
La correttezza del WFLOOD segue direttamente dalla correttezza del FLOODING per il broadcast, disponibile nella seguente lezione.
3.2 Complessità
Sia \(k\) il numero di nodi inizialmente nello stato \(\text{awake}\), ovvero \(|W| = k\). Troviamo le seguenti complessità
Message Complexity: Notiamo che ogni nodo inizialmente awake invia un messaggio a tutti i suoi vicini, mentre ogni nodo inizialmente asleep invia un messaggio a tutti i suoi vicini meno il vicino che l'ha fatto svegliare. Il numero di messaggi totali inviati è quindi
\[\sum\limits_{u \in W} |N(u)| + \sum\limits_{u \in V \setminus W} \Big(|N(u)| - 1\Big) = -(n-k) + 2m = 2m -n +k\]
dunque il caso peggiore è quando \(k=n\), ovvero quando tutti i nodi sono inizialmente svegli. Inizialmente infatti i nodi non sono sincronizzati tra loro rispetto a chi è sveglio e chi sta dormendo.
Ideal Time Complexity: Il tempo ideale di completamento invece è sempre pari al diametro della rete, esattamente come nell'analisi del protocollo flooding.
3.3 Esercizio: WFLOOD in un albero
Supponiamo di eseguire il protocollo WFLOOD su una rete ad albero \(T\). Siamo interessati a calcolare la message complexity dell'esecuzione del protocollo. In particolare, vogliamo far vedere come
\[Msg(\text{WFLOOD}/\text{Tree}) = n + k - 2\]
per dimostrare questo basta notare che in un albero abbiamo \(m = n-1\) archi. Dunque,
\[\begin{split} Msg(\text{WFLOOD}/\text{Tree}) &= 2 \cdot m - n + k \\ &= 2(n-1) + k -n \\ &= n + k - 2 \end{split}\]
\[\tag*{$\checkmark$}\]
4 Lower Bound per il Wake Up
Per quanto riguarda il problema del wake-up, abbiamo che, sotto le restrizioni \(R = \{\text{TR}, \text{BL}, \text{CN}, \text{ID}\}\), la message complexity del problema del wake-up su grafi completi è \(\Omega(n \cdot \log n)\).
Notiamo che l'ultima restrizione aggiunta sta per \(\text{Initial Distinct values}\), ed esprime il fatto che le entità hanno dei nomi unici,
Per la dimostrazione si rimanda al libro del corso, a pagina 59.