ADRC - 07 - Saturation

1 Lecture Info

Data: [2018-11-08 gio]

In questa lezione abbiamo introdotto la tecnica della saturazione, che permette la risoluzione di svariati problemi in una rete distribuita con una topologia ad albero.

2 La Tecnica della Saturazione (o Link Election)

Consideriamo di lavorare in topologie ad albero in cui ogni nodo sa se è una foglia oppure un nodo interno. La tecnica della saturazione consiste nell'identificare una singola coppia di nodi adiacenti all'interno della rete. Una volta identificata, questa coppia di nodi è in grado di far partire altre computazioni, a seconda del particolare problema che si vuole risolvere. Detto in altri termini, la tecnica della saturazione permette di "eleggere" un particolare arco della rete, ed è quindi anche chiamata link election.

Tipicamente la tecnica della saturazione viene utilizzata per risolvere problemi distribuiti di varia natura. In questo senso la saturazione è inserita all'interno di un processo più grande, che può essere diviso nelle seguenti tre fasi:

Fase di Attivazione: In questa fase i nodi initiators attivano i restanti nodi della rete utilizzando un protocollo di $\text{WAKE-UP}$.
Fase di Saturazione: In questa case a partire dalle foglie si identifica una coppia unica di nodi adiacenti.
Fase di Risoluzione: La coppia di nodi saturati scelti nella fase precedente fanno partire una o più computazioni necessarie alla risoluzione dello specifico problema di interesse.

Volendo formalizzare le prime due fasi del processo descritto in precedenza, procediamo definendo il problema $P = \langle P_{init}, P_{final}, R\rangle$, dove

$P_{init} := \text{Tutti i nodi sono AVAILABLE}$

$P_{final} := \begin{cases} \text{Tutti i nodi tranne due sono ACTIVE.} \\ \text{I due nodi restanti sono SATURATED e adiacenti.} \end{cases}$

$R = \begin{cases} \text{Total Reliability (TR)} \\ \text{Bidirectional Link (BL)} \\ \text{Connectivity (CN)} \\ \text{Knowledge of the Topology} \\ \text{Message Ordering (MO)} \\ \end{cases}$

Andiamo quindi a descrivere un protocollo che risolve questo specifico problema.

2.1 Protocollo FULL-SATURATION

Per quanto riguarda gli stati abbiamo la seguente situazione:

$S = \{\text{AVAILABLE}, \text{ACTIVE}, \text{PROCESSING}, \text{SATURATED}\}$
$S_{init} = \{\text{AVAILABLE}\}$

Le regole sono invece descritte a seguire

Notiamo che nel protocollo il concetto di parent viene utilizzati in due modi diversi. Nello stato $\text{AVAILABLE}$ per parent si intende il padre di un nodo foglia, ovvero l'unico nodo adiacente al nodo foglia. Nello stato $\text{ACTIVE}$ invece il parent di un nodo $x$ rappresenta l'unico nodo adiacente che ancora non ha inviato il messaggio $(M)$ al nodo $x$.

2.1.1 Correttezza

Per argomentare la correttezza del protocollo dobbiamo argomentare il fatto che esattamente due nodi passano dallo stato $\text{PROCESSING}$ allo stato $\text{SATURATED}$, e che questi due nodi sono anche adiacenti.

Dimostrazione: Iniziamo notando le seguenti cose:

Un nodo passa nello stato di $\text{PROCESSING}$ solo dopo che ha mandato il messaggio $(M)$ al suo parent.
Un nodo passa nello stato di $\text{SATURATED}$ solo dopo che riceve il messaggio $(M)$ dal suo parent.

Sia quindi $x$ un nodo arbitrario, e consideriamo il cammino percorso dai messaggi $M$

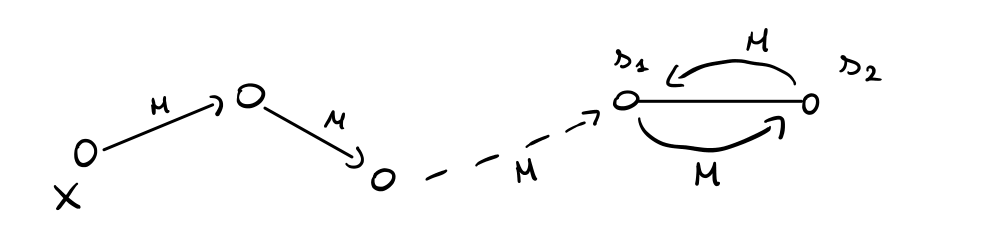
Dato che nel grafo non ci sono cicli, ad un certo punto dobbiamo necessariamente incontrare nel cammino un nodo $s_1$ che si trova nello stato $\text{SATURATED}$, in quanto ha ricevuto dal suo parent, il nodo $s_2$, il messaggio $M$. Ma allora quando $s_2$ riceve da $s_1$ il messaggio $(M)$ anche $s_2$ diventa $\text{SATURATED}$. Dunque il protocollo trova sempre almeno due nodi adiacenti $\text{SATURATED}$.

Notiamo inoltre che i nodi $\text{SATURATED}$ sono esattamente due. Infatti, se per assurdo fossero tre, diciamo $x, y$ e $z$, allora data la topologia ad albero, due di questi non sono adiacenti. Ma quindi

ovvero deve esistere un nodo che invia il messaggio $(M)$ a due archi, il che è impossibile.

\[\tag*{$\Huge\unicode{x21af}$}\]

Osservazione: Notiamo in ogni caso che la scelta di quali nodi vengono saturati dal protocollo dipende dal ritardo dei messaggi. Questo significa che potenzialmente ogni coppia di nodi adiacenti può essere la coppia saturata.

2.1.2 Complessità

Per quanto riguarda la message complexity, andando a suddividere il processo nelle sue varie fasi troviamo i seguenti messaggi

Nella fase di attivazione, seguendo la complessità del protocollo WAKE-UP e considerando che in un albero $m=n-1$, vengono spesi $n + k_{\star} -2$ messaggi, dove $k_{\star}$ indica il numero di initiators.

Nella fase di saturazione vengono invece spesi solamente $n$ messaggi.

Troviamo quindi un costo di totale di $2n + k_{\star} - 2$ messaggi.

2.2 Protocollo SATURATION PLUG-IN

Come abbiamo già menzionato molto spesso la saturazione è solo la seconda fase di un processo più grande. Andiamo adesso a presentare un template, detto anche protocollo "plug-in", che può essere poi specializzato per la risoluzione di vari problemi.

Le procedure invece hanno il seguente template

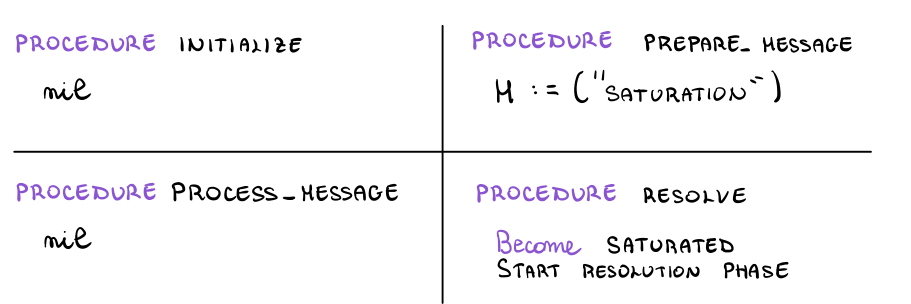
L'idea di questo plug-in protocol è che fornendo le implementazioni alle varie procedure assieme all'eventuale introduzione di particolari regole per gestire la fase di risoluzione siamo in grado di risolvere varie tipologie di problemi tramite la tecnica della saturazione. Questo sarà il tema della successiva sezione.

3 Applicazioni della Saturazione

La tecnica della saturazione può essere utilizzata per risolvere vari problemi computazionali in modo distribuito. Segue quindi qualche esempio in cui andiamo a fornire le implementazioni delle procedure lasciate vuote dal protocollo plug-in discusso prima per risolvere vari problemi.

3.1 Calcolo del Minimo

Consideriamo la situazione in cui ogni nodo inizialmente ha un valore $x$, e alla fine vuole sapere se tale valore è il valore minimo oppure no. Assumiamo che i valori non necessariamente sono distinti. Possono dunque esistere più valori di minimo.

Notiamo che in un rooted-tree in cui abbiamo identificato una radice il problema risulta banale. In questo ambiente basta infatti inviare il proprio valore alla radice, che calcola il minimo e poi lo distribuisce nella rete, in modo da far capire ad ogni nodo se il proprio valore è il minimo oppure no.

In un albero generico però le cose si complicano. In questo caso per risolvere il problema possiamo far ricorso alla saturazione, in nel messaggio $(M)$ inseriamo anche il valore minimo calcolato fino a quel momento.

Le procedure viste prima del protocollo plug-in vengono quindi implementate come segue

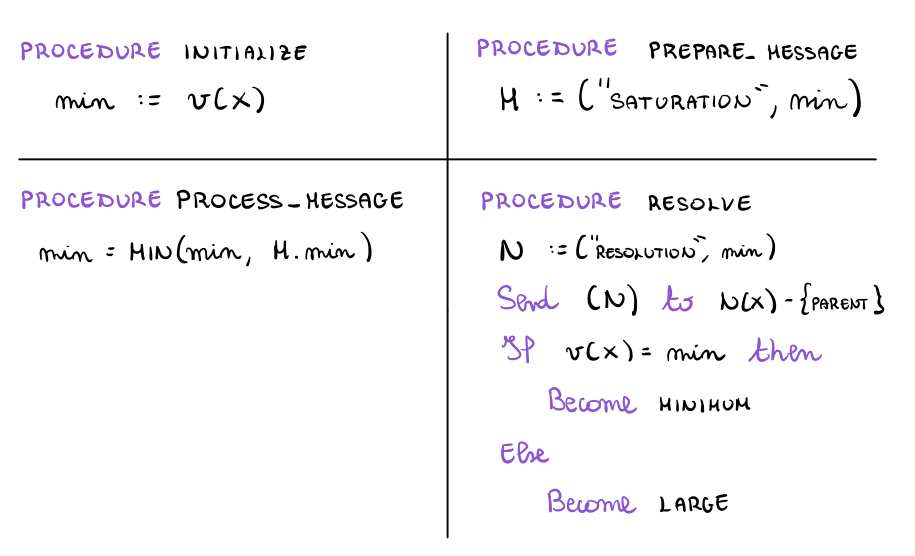
per gestire la fase di risoluzione viene poi introdotta la seguente regola

In termini di message complexity troviamo $2n + k_{\star} - 2$ messaggi inviati per la saturazione e $n-2$ messaggi inviati per la risoluzione finale. In totale quindia bbiamo $3n + k_{\star} - 4$ messaggi inviati.

3.2 Calcolo di Funzioni Distribuito

Generalizzando quanto visto prima, la saturazione può essere utilizzata per calcolare una qualsiasi funzione $F(\cdot)$ rispetto ai valori dei nodi, patto che $F$ sia una operazione di semi-gruppo, ovvero che rispetta le seguenti proprietà

Associatività: $F(F(a, b), c) = F(a, F(b, c))$
Commutatività: $F(a, b) = F(b, a)$

Operazioni di questo tipo sono ad esempio il massimo $(\max)$, il minimo $(\min)$, la somma $(\sum)$, il prodotto $(\prod)$ e i connettori logici come l'and $(\land)$, l'or $(\lor)$ e il not $(\neg)$.

In questo caso le procedure viste prima del protocollo plug-in vengono quindi implementate come segue

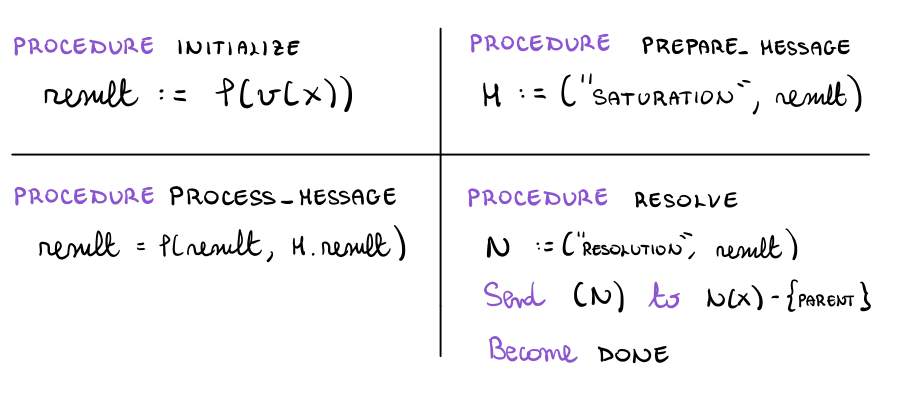
nuovamente, per gestire la fase di risoluzione introduciamo la seguente regola

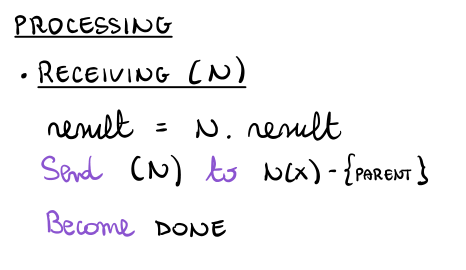
3.3 Calcolo della Media

Il calcolo della media può essere effettuato sempre tramite la saturazione. Questa volta i messaggi $(M)$ sono utilizzati per calcolare sia il numero dei nodi e sia la somma del valore dei nodi.

Una volta che queste informazioni vengono passate ad uno dei due nodi saturati, si è in grado di calcolare il valore medio tra tutti i valori dei nodi.

Osservazione: A differenza da quello che potrebbe sembrare, conoscere il parametro $n$ in un ambiente distribuito non è sempre un problema facile da risolvere.

Per risolvere il problema del calcolo della media le procedure del protocollo plug-in sono implementate come segue

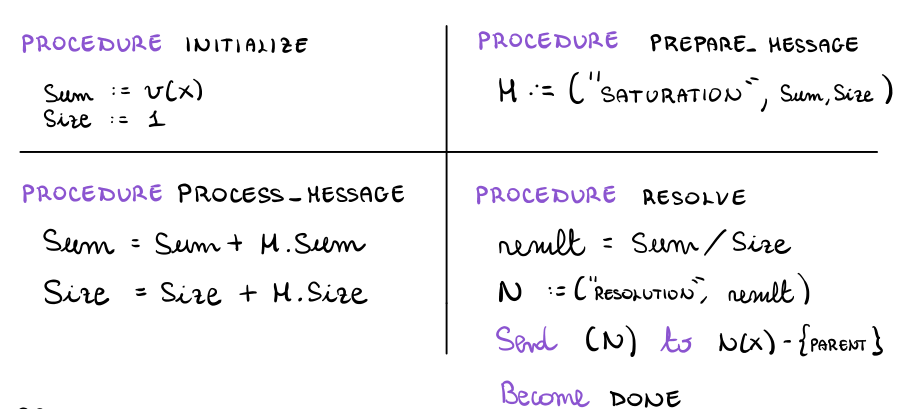
La fase di risoluzione invece viene gestita introducendo la seguente regola

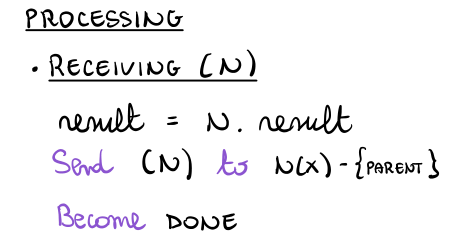
3.4 Calcolo delle Eccentricità

Sia $d(x, y)$ la distanza tra $x$ e $y$ nella nostra rete. Definiamo l'eccentricità di un nodo $x$ come la massima distanza tra $x$ e un qualsiasi altro nodo della rete. In formula,

\[r(x) := \max_{y \in V} \{\,\, d(x, y) \,\, \}\]

Il calcolo di $r(x)$ ci permette di capire quanto "centrale" un nodo è nella rete.

Andiamo adesso ad analizzare dei protocolli che ci permettono di calcolare in modo distribuito l'eccentricità per ogni nodo della rete.

3.4.1 Protocollo 1 (senza saturazione)

Un primo approccio per calcolare $r(x)$ potrebbe essere il seguente

Il nodo $x$ invia una richiesta in $\text{BROADCAST}$ a tutti i nodi della rete. In questa richiesta viene aggiornato di volta in volta il numero di archi attraversati.
Le foglie dell'albero ottenuto ponendo $x$ come radice inviano un messaggio indietro a $x$ per comunicare quanto si trovano distanti da $x$. $\big(\text{CONVERGECAST}\big)$

Così facendo il nodo $x$ è in grado di collezionare tutte le distanze. Ciò gli permette di capire facilmente qual'è la distanza massima, ovvero qual'è la sua eccentricità. Ripetendo poi il procedimento per ogni nodo otteniamo la soluzione al nostro problema.

In termine di message complexity notiamo che il calcolo di $r(x)$ richiede $2 \cdot (n-1)$ messaggi. Il calcolo di tutte le eccentricità richiede quindi $2 \cdot (n^2 - n)$ messaggi.

3.4.2 Protocollo 2 (con saturazione)

Andiamo adesso a descrivere trovare un protocollo più efficiente per risolvere lo stesso problema. Questa volta il protocollo di interesse utilizza la saturazione per eleggere un particolare arco $(s_1, s_2)$. Graficamente,

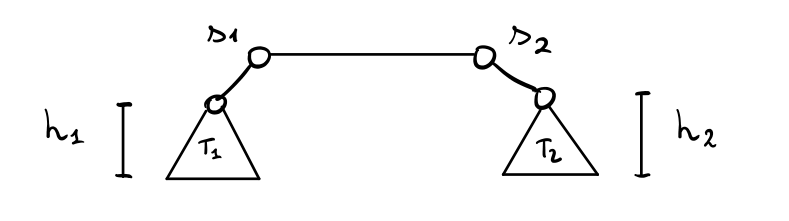
dove $h_1$ e $h_2$ sono rispettivamente le altezze dei sottoalberi $T_1$ e $T_2$. Queste altezze possono essere calcolare direttamente durante il processo di saturazione. Con queste informazioni i nodi $s_1$ e $s_2$ sono in grado di calcolare la loro eccentricità. Infatti,

$r(s_1) = \max \{h_1 + 1, h_2 + 2\}$
$r(s_2) = \max \{h_2 + 1, h_1 + 2\}$

Una volta calcolati $r(s_1)$ e $r(s_2)$ i nodi che si trovano a distanza $1$ da $s_1$ e $s_2$ sono in grado di calcolare a loro volta la loro eccentricità. Graficamente infatti troviamo

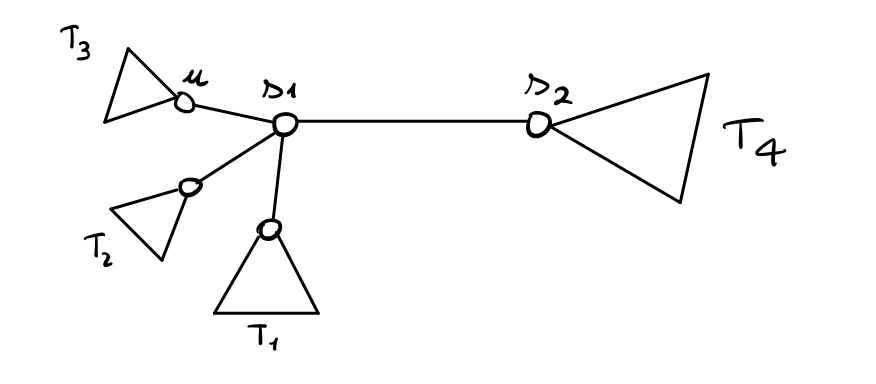
Notiamo che il nodo $u$ per calcolare la propria eccentricità deve ricevere dal nodo $s_1$ determinate informazioni. Il nodo $s_1$ non può semplicemente inviare a $u$ il valore $r(s_1)$, in quanto questo potrebbe introdurre degli errori nel calcolo di $r(u)$ nel caso in cui il nodo più distante da $s_1$ si trova proprio nell'albero $T_3$.

L'idea è quindi quella di mantenere nel nodo $s_1$ l'altezza di ogni sottoalbero radicato nel nodo. Queste informazioni vengono poi inviate al nodo $u$, che le può quindi utilizzare per calcolare la sua eccentricità nel seguente modo

\[r(u) = \max \{h_3, 1 + h_1, 1 + h_2, 2 + h_4\}\]

Applicando questo ragionamento in modo iterativo rispetto alla distanza dai nodi $s_1$ e $s_2$ si è in grado di calcolare l'eccentricità per tutti i nodi.

Segue l'implementazione delle procedure da inserire nel protocollo plug-in per il calcolo delle eccentricità

infine, la fase di risoluzione viene gestita dalla seguente regola

In termini di message complexity questo protocollo utilizza i messaggi inviati normalmente dalla saturazione, più i messaggi per effettuare il calcolo delle eccentricità. In totale troviamo

\[3n + k_{\star} - 4 \leq 4n - 4\]

dove $k_{\star}$ indica il numero di initiators

3.5 Calcolo dei Centri

Il nodo $c$ che minimizza l'eccentricità $r(x)$ è detto centro. La diametral path invece è la path semplice più lunga nel grafo. Consideriamo il problema di calcolare quali sono i centri di una rete.

Un primo approccio potrebbe essere il seguente:

Calcoliamo $r(x)$ per ogni $x \in V$.
Prendiamo il valore minimo $\underset{x \in V}{\min} \{\,r (x)\,\}$.

questo protocollo ha un costo di $6n - 6$. Per ottenere un protocollo più efficiente l'idea è quella di sfruttare le seguenti proprietà dei centri:

Proprietà 1: Un albero può avere o un solo nodo centrale oppure due nodi centrali che sono adiacenti.

Proprietà 2: I nodi centrali si trovano nelle diametral paths.

Proprietà 3: Sia $d_1[x]$ la massima distanza tra il nodo $x$ e un qualsiasi altro nodo, e sia $d_2[x]$ il secondo valore più alto di distanza tra $x$ e un qualsiasi altro nodo. Allora $x$ è un nodo centrale se e solo se

\[d_1[x] - d_2[x] \leq 1\]

Sfruttando queste proprietà è possibile definire il seguente protocollo per il calcolo dei centri:

Calcoliamo $r(x)$ per ogni $x \in V$.
Ogni nodo utilizza la proprietà $(3)$ per scoprire localmente se è o meno un centro.

Questo nuovo protocollo ha una message complexity di $4n - 4$.