ADRC - 08 - Leader Election
1 Lecture Info
Data:
In questa lezione abbiamo affrontato il problema della leader election in un ambiente distribuito.
\[\require{cancel}\]
2 Why do we need a Leader?
Nei sistemi distribuiti è fondamentale essere in grado di rompere la simmetria tra i vari nodi. Un modo per rompere la simmetria è tramite la risoluzione del problema della leader election. Il problema consiste nel partire da un insieme di initiators con l'obiettivo finale di eleggere un singolo nodo come leader e far diventare i restanti nodi dei followers del leader scelto.
Osservazione: In termini di simmetria notiamo che il grafo completo è la struttura simmetrica più densa, mentre l'anello è la struttura simmetrica più sparsa. L'albero invece non è una struttura simmetrica per la presenza delle foglie.
Prima di iniziare a trattare il problema però riportiamo il seguente risultato di impossibilità.
Teorema (Angluin, '80): Il problema della leader election non può essere risolto in modo generale se le entità non hanno diverse identità.
Dal teorema appena enunciato segue che per poter risolvere il problema necessitiamo della restrizione \(\text{UNIQUE-ID}\). Nella trattazione a seguire quindi per ogni nodo \(x \in V\) indichiamo con \(v(x)\) l'identità del nodo di \(x\). La restrizione \(\text{UNIQUE-ID}\) ci deve garantire che la funzione \(v(\cdot)\) è una funzione iniettiva, ovvero che
\[\forall x, y \in V: \,\,\, v(x) = v(y) \implies x = y\]
3 Election in Trees
Se ci restringiamo ad istanze la cui topologia è quella ad albero, il problema della leader election può essere facilmente risolto tramite l'utilizzo della saturazione, una tecnica che abbiamo introdotto nella precedente lezione.
L'idea infatti è quella di utilizzare la saturazione per calcolare il nodo con l'etichetta minimia. Tale nodo sarà eletto a leader, mentre i restanti diventeranno followers.
4 Election in the Ring
Consideriamo adesso un anello con \(n\) nodi ed \(n\) archi in cui i nodi condividono lo stesso concetto di direzione, intendendo con ciò che ogni nodo è in grado di distinguere la porta di destra da quella di sinistra. Graficamente,
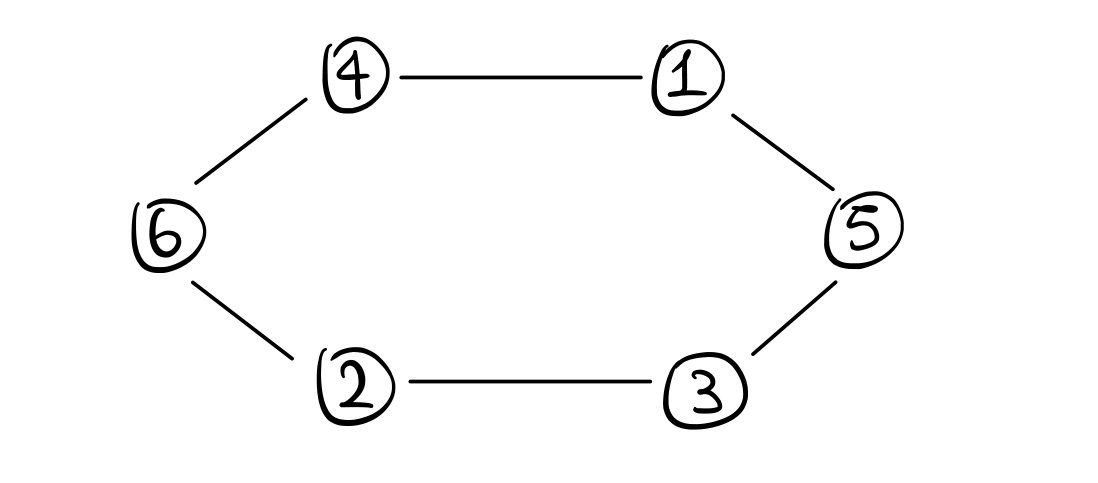
Andiamo adesso a discutere tre protocolli diversi che risolvono lo stesso problema.
4.1 Protocol 1: All the Way!
L'idea del primo protocollo, chiamato "all the way!" è quella di inviare ogni etichetta ad ogni nodo. Così facendo ogni nodo è in grado di calcolare l'etichetta minore. Il nodo a cui appartiene l'etichetta minore sarà il nodo leader, mentre gli altri saranno i followers.
Per poter effettuare il calcolo del minimo però ogni nodo deve sapere quanti nodi ci sono, ovvero deve conoscere il valore del parametro \(n\). Una volta che il nodo conosce tale valore infatti può aspettare di ricevere \(n\) etichette distinte, per poter calcolare poi il minimo globale e scegliere se diventare leader o follower.
Per fare in modo che ogni nodo calcoli il valore del parametro \(n\) l'idea è quella di far compiere un giro completo dell'anello alla sua etichetta. Nel messaggio contenente l'etichetta viene aggiunto un contatore, e ad ogni salto il contatore presente nel messaggio viene incrementato di \(1\) unità. Quando infine il nodo riceve il messaggio con la propria etichetta è in grado di stabilire il valore di \(n\) semplicemente leggendo il valore raggiunto dal contatore.
Notiamo che il protocollo appena descritto ha una message complexity di \(O(n^2)\), in quanto su ogni arco passano \(n\) messaggi distinti.
Osservazione: Il protocollo appena descritto funziona anche per collegamenti unidirezionali, e in realtà risolve il problema più generale della data collection.
4.2 Protocol 2: As Far as it Can!
Andando a modificare leggermente il protocollo descritto prima, l'idea del protocollo chiamato "as far as it can!" è sempre quella di propagare i messaggi, ma di eliminare la propagazione di messaggi superflui.
In particolare ogni nodo blocca tutti i messaggi che contengono etichette dal valore più grande di quella più piccola scoperta fino a quel momento.
In questo protocollo l'unico nodo che riceve la propria etichetta è quello con l'etichetta minima. Da questo segue che appena un qualsiasi nodo riceve la propria eticehtta diventa leader e informa gli altri nodi di diventare followers.
4.2.1 Message complexity
In termine di message complexity, anche se tendenzialmente questo protocollo utilizza meno messaggi di quello precedente, nel caso peggiore i due protocolli sono asintoticamente equivalenti. Consideriamo infatti la seguente istanza

Notiamo che a seconda del verso seguito dai messaggi, possiamo avere o il caso peggiore o il caso migliore. In particolare,
Se i messaggi seguono un verso antiorario, allora troviamo il caso peggiore, in quanto tutti i messaggi inviati possono essere scartati solo dal nodo con l'etichetta più piccola.
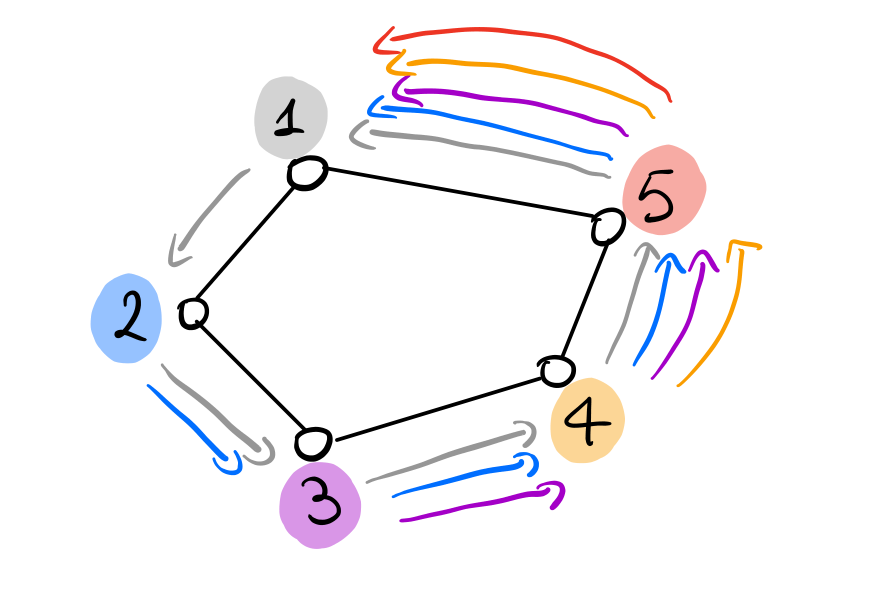
In questo caso abbiamo una message complexity di
\[n + (n-1) + \ldots + 2 + 1 = \frac{n(n+1)}{2}\]
Se i messaggi invece seguono un verso orario, allora troviamo il caso migliore, in quanto tutte le etichette tranne quella minima vengono bloccate subito.
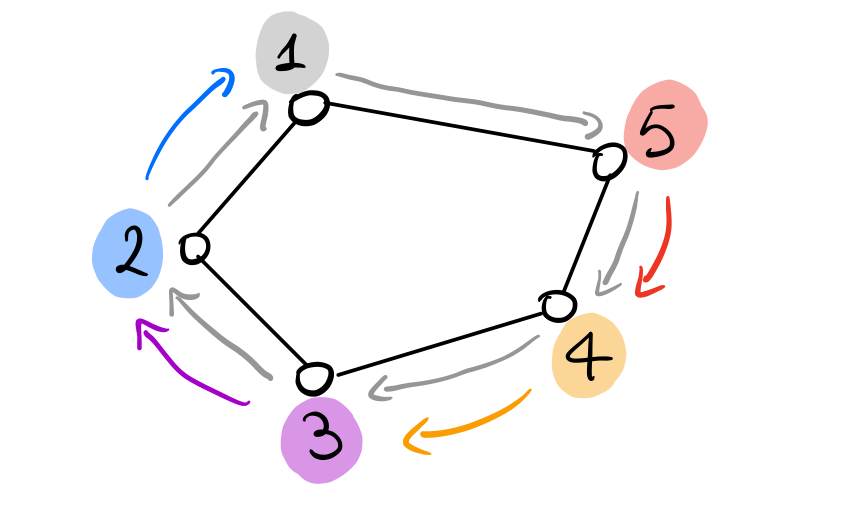
In questo caso abbiamo una message complexity di
\[n + (n-1) = 2n - 1\]
Possiamo quindi vedere come il protocollo appena descritto non è tanto migliore di quello precedente.
4.3 Protocol 3: Stage Technique
La stage technique è una tecnica ammortizzata che ci permette di propagare ogni etichetta in modo controllato.
Il protocollo è diviso in stages. Ogni nodo attivo nello stage \(i\) invia due messaggi, uno a destra e l'altro a sinistra. Entrambi i messaggi, detti messaggi "forth", contengono l'etichetta del nodo e percorrono una distanza di \(2^{i-1}\) passi prima di essere rispediti indietro al mittente sotto forma forma di messaggi "feedback". Quando un nodo con etichetta \(x\) riceve un messaggio con etichetta \(y\) possono succedere le seguenti due cose:
Se \(x < y\), allora il messaggio contenete \(y\) viene distrutto e il nodo che ha inviato quel messaggio non passa alla fase successiva;
Se \(y < x\), allora il nodo che ha ricevuto il messaggio si distrugge e non passa alla fase successiva.
Tutti i nodi che ricevono indietro entrambi i messaggi inviato nello stage \(i\) passano allo stage \(i+1\). Alla fine esisterà un solo nodo che riceverà da una porta il messaggio che aveva inviato dall'altra porta. Dato che tale nodo è unico ed esiste sempre, tale nodo sarà il nostro leader.
Osservazione: Durante l'esecuzione del protocollo è possibile che diversi nodi si trovino in diversi stages. L'unica cosa che ci importa è che i nodi devono rispettare l'ordine delle etichette e comportarsi come descritto in precedenza.
Da notare poi che il protocollo inizia con una fase di wake-up.
4.3.1 Correttezza e Terminazione
Notiamo che dopo un tempo finito il nodo con l'etichetta minima si deve necessariamente svegliare in un tempo finito. Una volta svegliato tale nodo, avendo l'etichetta minima, rispetterà la condizione descritta prima, ovvero ad un certo punto arriverà ad uno stage \(i^*\) in cui riceverà da una porta il messaggio che ha inviato dalla porta opposta. Tale stage \(i^*\) può essere calcolato. Infatti si ha che
\[i^* = \min_{i} \{\,\,2^{i-1} \leq n \,\,\} \iff i^* = \theta(\log_2{n})\]
Dunque il numero di stages necessari e sufficienti per far terminare il protocollo è \(\theta(\log_2{n})\). Dato che ogni stage dura un tempo finito, ne segue che il protocollo termina correttamente in un tempo finito.
4.3.2 Message Complexity
Per quanto riguarda la message complexity, l'idea è quella di contare quanti messaggi vengono inviati in ogni fase del protocollo. A tale fine definiamo la seguente quantità
\[n_i := \text{numero di nodi che hanno superato la fase } i - 1\]
Osserviamo poi che per poter superare la fase \(i-1\) un nodo deve necessariamente "ammazzare" i nodi che si trovano ad una distanza massima di \(2^{i-2}\) da lui, considerando entrambi i lati. Da questo segue che in ogni gruppo di \(2^{i-2} + 1\) nodi, al massimo uno di questi ha una possibilità di sopravvivere lo stage \(i-1\).

Troviamo quindi il seguente upper bound
\[n_i \leq \frac{n}{2^{i-2} + 1}\]
Da questo segue che i nodi attivi hanno una decrescita esponenziale.
Sia quindi \(i > 1\), e consideriamo i vari messaggi inviati nello stage \(i\). Nel caso peggiore troviamo la seguente situazione:
Forth messages: I messaggi di tipo "forth" inviati nello stage \(i\) percorrono una distanza di \(2^{i-1}\) passi in entrambe le direzioni. Dato che abbiamo \(n_i\) nodi inizialmente attivi, troviamo al più \(n_i \cdot 2 \cdot 2^{i-1}\) messaggi di tipo "forth".
Feedback messages: Per ogni nodo che sopravvive lo stage abbiamo \(2 \cdot 2^{i-1}\) messaggi di tipo "feedback". Ogni nodo che non sopravvive lo stage \(i\) invece ne potrà ricevere al massimo \(1\) messaggio di feedback. In totale quindi troviamo al massimo
\[n_{i+1} \cdot 2 \cdot 2^{i-1} + \underbrace{(n_i - n_{i+1})}_{\text{nodi uccisi nello stage } i} \cdot 2^{i-1}\]
messaggi di tipo "feedback".
Dunque, per ogni stage \(i > 1\), abbiamo che il totale dei messaggi inviati può essere maggiorato da
\[\begin{split} n_i \cdot 2 \cdot 2^{i-1} + n_{i+1} \cdot 2 \cdot 2^{i-1} + (n_i - n_{i+1}) \cdot 2^{i-1} &= 2^{i-1} \cdot (3 \cdot n_i + n_{i+1}) \\ &\leq 2^{i-1} \cdot \Big( 3 \cdot \left\lfloor \frac{n}{2^{i-2} + 1}\right\rfloor + \left\lfloor \frac{n}{2^{i-1} + 1}\right\rfloor \Big) \\ &< \frac{3n \cdot 2^{i-1}}{2^{i-2} + 1} + \frac{n \cdot 2^{i-1}}{2^{i-1} + 1} \\ &< \frac{3n \cdot 2^{i-1}}{2^{i-2} + 1} + \frac{n \cdot \cancel{2^{i-1}}}{\cancel{2^{i-1}}} \\ &= 6n + n \\ &= 7n \end{split}\]
Per quanto riguarda il primo stage invece \((i = 1)\), il caso peggiore è quando tutti sono initiators. In questo caso si ha che
\[ n_2 \leq \frac{n}{2^0 + 1} = \frac{n}{2}\]
I nodi che sopravvivono hanno un costo individuale di
\[\begin{cases} 2 \text{ per msg "forth"} \\ 2 \text{ per msg "feedback"} \end{cases} \implies 4 \cdot n_2 \text{ messaggi totali}\]
Gli altri invece, quelli che non sopravvivono, hanno un costo individuale di
\[\begin{cases} 2 \text{ per msg "forth"} \\ 1 \text{ per msg "feedback"} \end{cases} \implies 3 \cdot (n - n_2) \text{ messaggi totali}\]
In totale quindi troviamo
\[4n_2 + 3n - 3n_2 = n_2 + 3n < 4n\]
mettendo tutto assieme il totale dei messaggi inviati è
\[\begin{split} M(\text{STAGE TECHNIQUE}) &\leq \sum_{i = 1}^{\log n} 7n + \theta(n) \\ &= 7n \cdot \log{n} + \theta(n) \\ &= \theta(n \cdot \log{n}) \end{split}\]
Dunque,
\[M(\text{STAGE TECHNIQUE}) = O(n \cdot \log{n})\]