AGT - 02 - Global Connection Game
1 Network Formation Games
I network formation games modellano il modo in cui degli agenti egoistici creano e utilizzano le reti. In particolare noi vedremo due giochi di questo tipo, che sono
Global Connection Game (GCG);
Local Connection Game (LCG);
In entrambi i casi i giocatori vogliono costruire una rete che sia utile ai loro obiettivi cercando nel contempo di pagare il meno possibile. I NFGs pososno essere utilizzati per modellare varie situazioni, tra cui:
Formazioni nei social networks;
Formazioni di sottoreti in reti di calcolatori;
Per analizare questi giochi utilizzeremo il concetto di NE per rappresentare una soluzione del gioco. Una rete che corrisponde ad un NE è detta stabile. Infine, per valutare la qualità di una soluzione utilizzeremo il costo sociale inteso come la somma dei costi dei giocatori. Il nostro obiettivo è quindi quello di dare un upper bound alla perdità di efficenza risultante dalla stabilità in un setting egoistico.
2 Global Connection Game
Il Global Connection Game (GCG) è stato introdotto nell'articolo del 2004 intitolato "The Price of Stability for Network Design with Fair Cost Attribution" ed è così descritto
Abbiamo un grafo diretto \(G = (V, E)\) in cui ad ogni arco \(e \in E\) è associato un costo (non-negativo) \(C_e \in \mathbb{R^+}\).
Ci sono poi \(k\) giocatori, e ad ogni giocatore è associato un nodo sorgente \(s_i\) e un nodo destinazione \(t_i\). L'obiettivo di ogni giocatore è quello di costruire una rete in cui il nodo destinazione \(t_i\) è raggiungibile dal nodo sorgente \(s_i\), cercando di pagare il meno possibile. A tale fine la strategia del giocatore \(i\) è la scelta di un path \(P_i\) da \(s_i\) a \(t_i\).
Dato un vettore di strategie di \(S\), chiamato anche profilo di strategie o semplicemente profilo, il grafo costruito sarà dato dall'unione delle paths scelte da tutti i giocatori, e verrà indicato con
\[N(S) := \bigcup_i P_i\]
Il costo costo di costruzione della rete è condiviso tra i giocatori nel seguente modo
\[\text{COST}_i(S) := \sum\limits_{e \in P_i} \frac{C_e}{K_e(C)}\]
dove \(K_e(S)\) indica il numero di giocatori che hanno scelto l'arco \(e\).
Osservazione: Lo schema di condivisione del costo utilizzato è chiamato fair o anche Shapley cost-sharing mechanism.
2.1 Esempi
Per iniziare andiamo a vedere qualche esempio di questo gioco.
Esempio 1: Consideriamo la seguente rete \(G=(V,E)\)
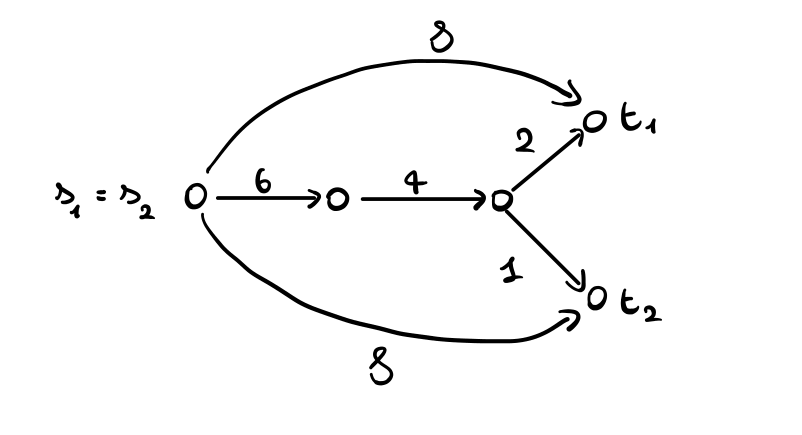
Notiamo che se entrambi i giocatori scelgono la path centrale, abbiamo che il primo giocatore \(a_1\) paga \(7\) mentre il secondo \(a_2\) paga \(6\). Questa situazione è un NE il cui costo sociale è ottimo.
La situazione però cambia se modifichiamo i pesi nel seguente modo
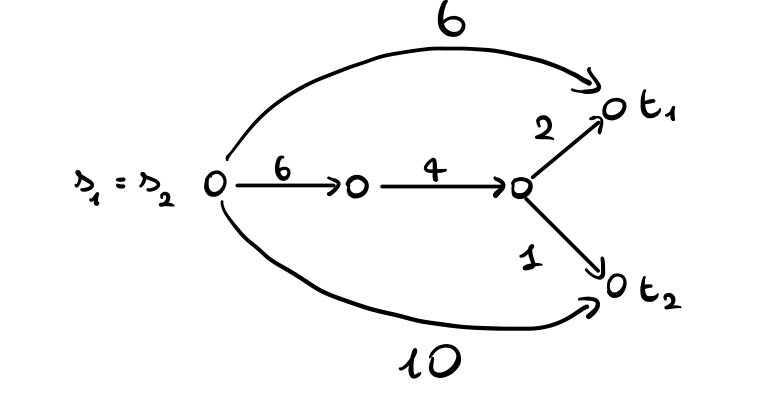
In questo caso l'ottimo sociale rimane sempre la situazione in cui \(a_1\) e \(a_2\) scelgono il path centrale, il cui costo è \(6 + 4 + 1 + 2 = 13\). Tale situazione però non è più un NE, in quanto ad \(a_1\) conviene pagare l'arco diretto \((s_1, t_1)\).
È possibile osservare che con questa nuova pesatura l'unico NE è quello in cui entrambi i giocatori comprano i rispettivi archi diretti. Il costo sociale di questa soluzione è \(10 + 6 = 16\).
Esempio 2: Sia adesso \(G=(V,E)\) la rete così fatta
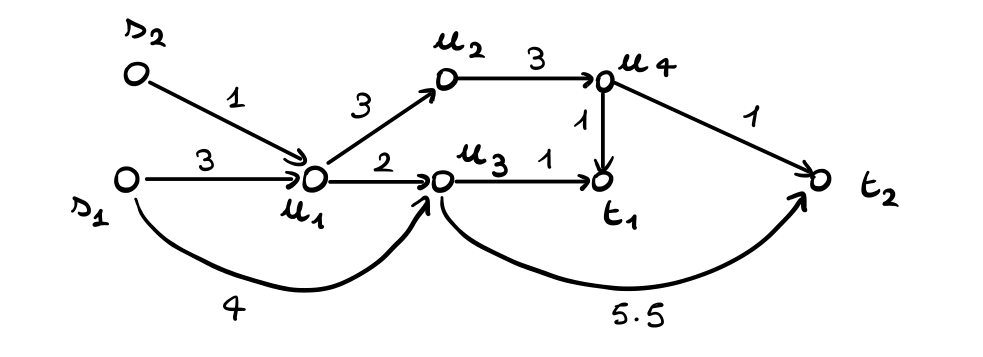
e consideriamo il seguente profilo di strategie
\[S = \begin{cases} a_1: \, &s_1 \to u_1 \to u_2 \to u_4 \to t_1 \\ a_2: \, &s_2 \to u_1 \to u_2 \to u_4 \to t_2 \\ \end{cases} \implies \begin{align} \text{COST}_1(S) &= 3 + 1.5 + 1.5 + 1 = 7 \\ \text{COST}_2(S) &= 1 + 1.5 + 1.5 + 1 = 4 \\ \end{align}\]
Notiamo che tale profilo non è un NE, in quanto il giocatore \(a_1\) può migliorare il suo costo utilizzando il nodo \(u_3\) al posto del nodo \(u_2\), ottenendo il seguente profilo
\[S = \begin{cases} a_1: \, &s_1 \to u_1 \to u_3 \to t_1 \\ a_2: \, &s_2 \to u_1 \to u_2 \to u_4 \to t_2 \\ \end{cases} \implies \begin{align} \text{COST}_1(S) &= 3 + 2 + 1 = 6 \\ \text{COST}_2(S) &= 1 + 3 + 3 + 1 = 8 \\ \end{align}\]
Nuovamente, questo profilo non è un NE, in quanto adesso è il giocatore \(a_2\) che può migliorare
\[S = \begin{cases} a_1: \, &s_1 \to u_1 \to u_3 \to t_1 \\ a_2: \, &s_2 \to u_1 \to u_3 \to t_2 \\ \end{cases} \implies \begin{align} \text{COST}_1(S) &= 3 + 1 + 1 = 5 \\ \text{COST}_2(S) &= 1 + 1 + 5.5 = 7.5 \\ \end{align}\]
Adesso nessuno può migliorare. Abbiamo quindi trovato un NE con un costo sociale di \(12.5\).
2.2 Obiettivi Analisi
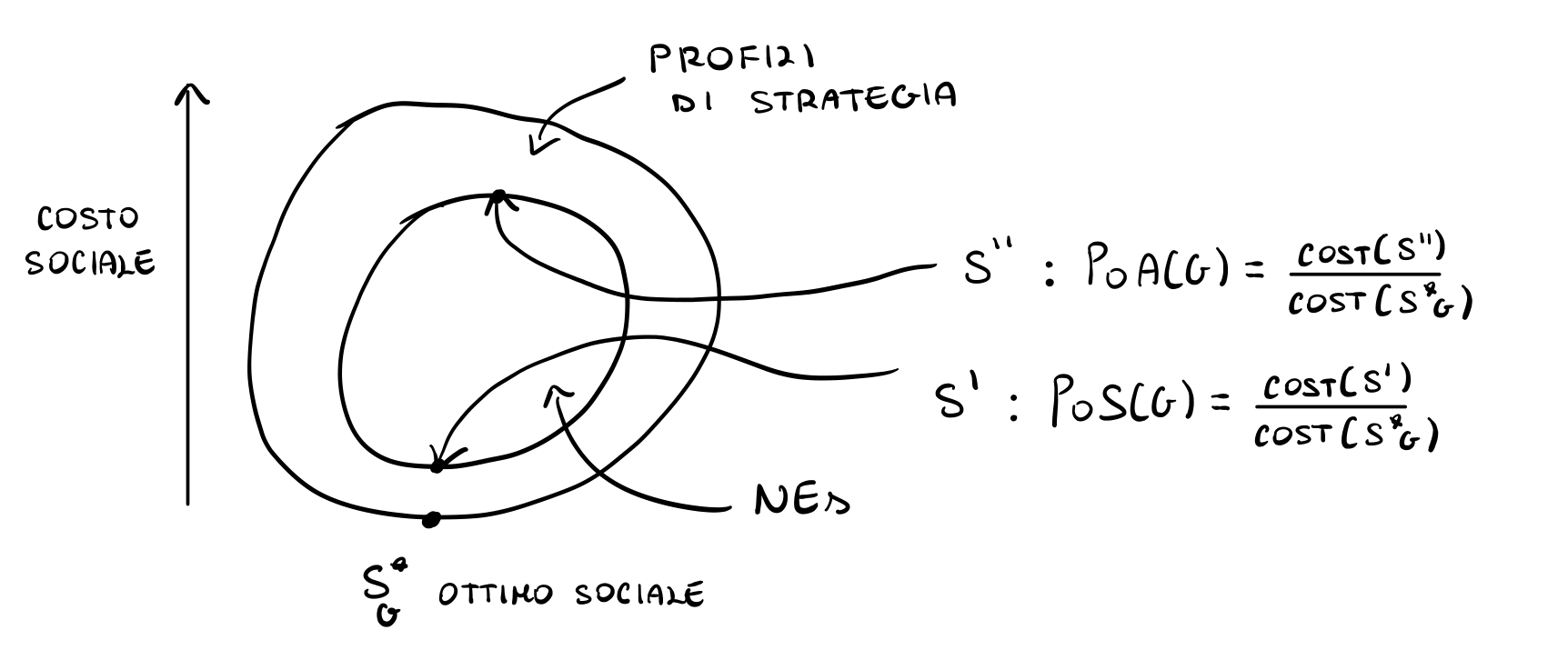
Fissata una rete \(G\), sia \(S_G^*\) il vettore di strategie ottimo rispetto al costo sociale. Definiamo quindi le seguenti quantità
Il PoA del gioco in \(G\) è dato da
\[\underset{\text{S: S è NE}}{\max} \frac{\text{COST}(S)}{\text{COST}(S^*_G)}\]
Il PoS del gioco in \(G\) è dato da
\[\underset{\text{S: S è NE}}{\min} \frac{\text{COST}(S)}{\text{COST}(S^*_G)}\]
Graficamente troviamo la seguente situazione
Dato che vogliamo limitare il PoS e PoA nel caso peggiore, al posto di considerarli solamente fissato un particolare grafo \(G\) definiamo
PoA del gioco come \(\underset{G}{\max} \text{PoA in G}\)
PoS del gioco come \(\underset{G}{\max} \text{PoS in G}\)
Le domande a cui vogliamo rispondere rispetto a questo gioco sono le seguenti
Esiste sempre un NE?
Possiamo dare un bound al PoA?
Possiamo dare un bound al PoS?
Giocando in modo ripetuto con la better response dynamics, riusciamo sempre a convergere ad una rete stabile?
Notazione: Durante l'analisi per rappresentare i profili di strategie utilizzeremo le seguenti notazioni
\(X = (x_1, x_2, \ldots, x_k)\)
\(X_{-i} = (x_1, x_2, \ldots, x_{i-1}, x_{i+1}, \ldots, x_k)\)
\(X = (x_{i-1}, x_i)\)
Notiamo come il vettore \(X_{-i}\) contiene le strategie di tutti i giocatori tranne che quella del giocatore \(i\).
2.3 PoA
Cominciamo analizzando il PoA (Price of Anarchy).
2.3.1 Lower Bound
Per dare un lower bound al PoA l'idea è quella di costruire un particolare grafo \(G\) che contiene un NE tale che
\[\frac{\text{COST}}{\text{COST}(S^*_G)} = k\]
con \(k\) numero di giocatori. Così facendo infatti abbiamo che \(\text{PoA} \geq k\).
Il grafo che vogliamo è il seguente
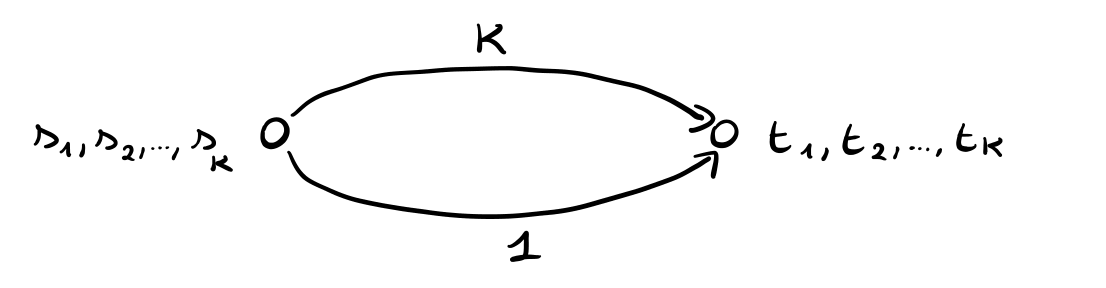
Notiamo come l'ottimo sociale del grafo è quello in cui tutti scelgono l'arco inferiore. Il costo di tale ottimo è \(1\). Un NE però è dato dal profilo in cui tutti i nodi scelgono l'argo superiore. Il costo di questo NE è invece \(k\).
\[\tag*{$\checkmark$}\]
2.3.2 Upper Bound
Vale il seguente
Teorema: Il PoA nel Global Connection Game (GCG) con \(k\) giocatori è al più \(k\).
Dimostrazione: Sia \(S\) un NE e sia \(S^*\) un profilo di strategie che minimizza il costo sociale. Per ogni giocatore \(i\) consideriamo \(\pi_i\), la shortest path in \(G\) che collega \(s_i\) a \(t_i\). Seguono quindi una serie di disuguaglianze
Dal fatto che \(S\) è un NE, al giocatore \(i\) non conviene cambiare strategia
\[\text{COST}_i(S) \leq \text{COST}_i(S_{-i}, \pi_i)\]
Nel caso peggiore il giocatore \(i\) deve comprare tutti gli archi del cammino \(\pi_i\) da solo
\[\text{COST}_i(S_{-i}, \pi_i) \leq d_G(s_i, t_i)\]
Il costo sociale è la somma del costo di tutti gli archi comprati
\[COST(S^*) = \sum\limits_{i = 1}^k \text{COST}_i(S^*) = \sum\limits_{i = 1}^k \sum\limits_{e \in P_i} \frac{C_e}{K_e(S^*)} = \sum_{e \in N(S^*)} \cancel{K_e(S^*)} \cdot \frac{C_e}{\cancel{K_e(S^*)}}\]
Dato poi che l'ottimo sociale deve contenere per forza un qualsiasi cammino \(\pi\) che collega \(s_i\) a \(t_i\), segue che
\[d_G(s_i, t_i) \leq \text{cost of } \pi \leq \text{COST}(S^*)\]
Mettendo tutto assieme troviamo che
\[\text{COST}_i(S) \leq \text{COST}_i(S_{-i}, \pi_i) \leq d_G(s_i, t_i) \leq \text{COST}(S^*)\]
Infine, sommando per ogni giocatore,
\[\text{COST}(S) = \sum\limits_{i = 1}^k \text{COST}_i(S) \leq k \cdot \text{COST}(S^*)\]
\[\tag*{$\blacksquare$}\]
2.4 PoS
Continuiamo analizzando il PoS (Price of Stability).
2.4.1 Lower Bound
Per ogni \(\epsilon > 0\) piccolo consideriamo il seguente grafo
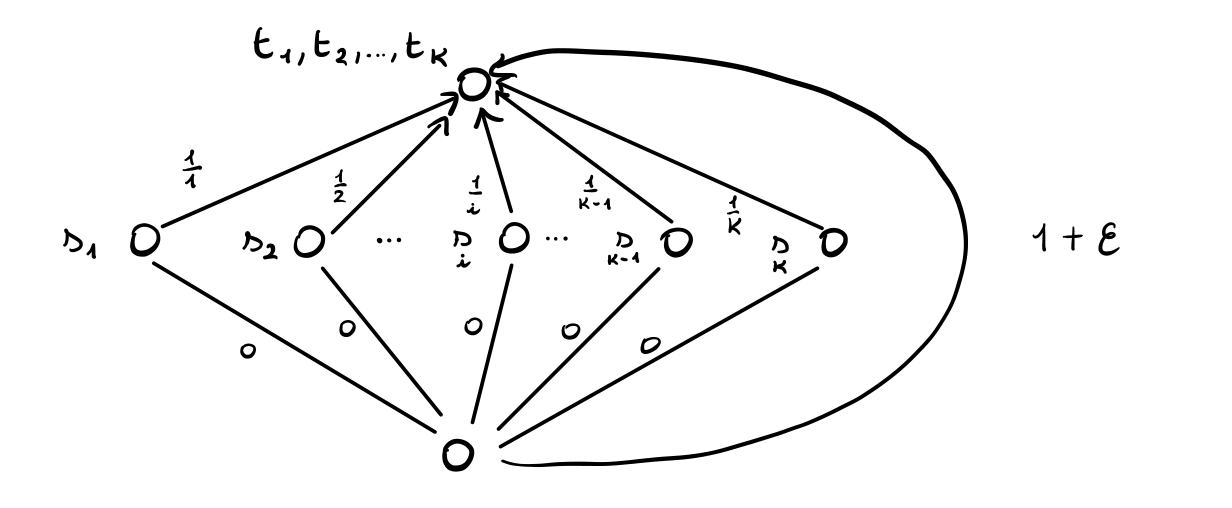
Notiamo che l'ottimo sociale ha un costo di \(1 + \epsilon\). Questo stato però non è un equilibrio di nash, in quanto al giocatore \(k\) conviene comprare l'arco diretto \((s_k, t_k)\) e pagare \(1/k\) al posto di \((1+\epsilon)/k\). Iterando questo ragionamento si può vedere che l'unico equilibrio in questo grafo è il profilo in cui ciascun giocatore sceglie di pagare l'arco diretto. Questo equilibrio ha un costo di
\[\sum\limits_{i = 1}^k \frac{1}{i} =: H_k \leq \ln k + 1\]
dove \(H_k\) è il \(k\) -esimo numero armonico.
Il PoS per questo particolare esempio è quindi
\[\text{PoS} \geq \frac{H_k}{1 + \epsilon}\]
che per \(\epsilon \to 0\) diventa \(\text{PoS} \geq H_k\).
2.4.2 Upper Bound
Al fine di ottenere un upper bound per il PoS utilizzeremo una tecnica chiamata potential function method. Si rimanda quindi alla sezione Potential Function Method in cui si dimostrano i risultati generali che andiamo ad utilizzare per il nostro caso particolare.
Al fine di applicare i risultati della funzione potenziale al GCG definiamo la seguente funzione
\[\forall \text{ profilo } S: \Phi(S) := \sum\limits_{e \in E} \Phi_e(S) = \sum\limits_{e \in E} C_e \cdot H_{K_e(S)}\]
dove \(K_e(S)\) è il numero di giocatori in \(S\) che hanno scelto l'arco \(e\), e \(H_i\) è l'i-esimo numero armonico, definito come segue
\[H_i := \begin{cases} \sum\limits_{j = 1}^i \frac{1}{j} \,\,&,\,\, i > 0 \\ 0 \,\,&,\,\, i = 0 \\ \end{cases}\]
Andiamo adesso a dimostrare che \(\Phi\) è una exact potential function per il gioco GCG.
Lemma 1: Sia \(S = (P_1, P_2, \ldots, P_k)\) e sia \(P_{i}^{'}\) un path alternativo per il giocatore \(i\). Allora, se consideriamo il nuovo profilo \(S^{'} = (S_{-i}, P_i^{'})\) troviamo
\[\Phi(S) - \Phi(S') = \text{COST}_i(S) - \text{COST}_i(S')\]
Dimostrazione: Andiamo a far vedere che per ogni arco \(e \in E\), la differenza di potenziale dell'arco \(e\) nelle due strategie \(S\) e \(S'\) è uguale alla differenza del costo dell'arco \(e\) nelle due strategie.
Iniziamo notando che banalemente, per ogni arco \(e\) tale che \(e \in P_i \cap P_{i}^{'} \lor (e \not \in P_i \land e \not \in P_{i}^{'})\), il potenziale di \(e\) nelle due strategie è lo stesso, come è lo stesso il contributo nel costo del giocatore \(i\) rispetto l'arco \(e\).
Consideriamo adesso gli archi \(e \in P_i \setminus P_{i}^{'}\), ovvero gli archi che prima venivano selezionati e che adesso non sono più selezionati dal giocatore \(i\). Per ogni arco del genere il giocatore risparmia \(C_e/K_e(S)\) nella nuova strategia \(S'\). Questo risparmio lo troviamo riflesso nella differenza del potenziale di \(e\) nelle due strategie. Troviamo infatti che
Il contributo di \(e\) nel potenziale di \(S\) è
\[\Phi_e(S) = C-e \cdot \Big(1 + \frac12 + \ldots + \frac{1}{K_e(S) - 1} + \frac{1}{K_e(S)} \Big)\]
Il contributo di \(e\) nel potenziale di \(S'\) è
\[\Phi_e(S) = C-e \cdot \Big(1 + \frac12 + \ldots + \frac{1}{K_e(S) - 1} \Big)\]
E quindi la differenza tra i due potenziali è
\[\Phi_e(S) - \Phi_e(S') = \frac{C_e}{K_e(S)}\]
che è proprio la differenza del costo delle due strategie \(S\) e \(S^{'}\) rispetto all'arco \(e\).
Notiamo infine come lo stesso ragionamento può essere effettuato per gli archi \(e \in P_{i}^{'} \setminus P_i\), stando attenti che in questo caso la differenza di potenziale (e quindi di costo) è di \(C_e/(K_e(S) + 1)\).
\[\tag*{$\blacksquare$}\]
Siamo ora in grado di dimostrare l'upper bound per il PoS. Vale infatti il seguente
Lemma 2: Per ogni profilo \(S\) vale
\[\text{COST}(S) \leq \Phi(S) \leq H_k \cdot \text{COST}(S)\]
Dimostrazione: Ricordiamo che \(\text{COST}(S) = \sum_{e \in N(S)} C_e\), ovvero il costo sociale del profilo \(S\) è dato dalla somma dei pesi degli archi utilizzati. Tale somma può essere maggiorata nel seguente modo
\[\text{COST}(S) = \sum\limits_{e \in N(S)} C_e \leq \sum\limits_{e \in E} C_e \cdot H_{K_e(S)} = \Phi(S)\]
in quanto se \(e \in E\) non è utilizzato, allora \(H_{K_e(S)} = H_0 = 0\), mentre se \(e \in N(S)\), allora
\[K_e(S) \geq 1 \implies H_{K_e(S)} \geq 1 \implies C_e \leq C_e \cdot H_{K_e(S)}\]
Inoltre, notando che ci sono al massimo \(k\) giocatori, e quindi che per ogni \(e \in N(S): 1 \leq K_e(S) \leq k\), segue che
\[\Phi(S) = \sum\limits_{e \in E}C_e \cdot H_{K_e(S)} = \sum\limits_{e \in N(S)} C_e \cdot H_{K_e(S)} \leq \sum\limits_{e \in N(S)} C_e \cdot H_k = H_k \cdot \text{COST}(S)\]
\[\tag*{$\blacksquare$}\]
Utilizzando i risultati della teoria generale delle funzioni potenziale quindi siamo in grado di concludere i seguenti risultati
Teorema: Ogni istanza del GCG ha un punto NE, che può essere ottenuto giocando in modo ripetuto con la better response dynamics.
Teorema: Il PoS del GCG giocato con \(k\) giocatori è al più \(H_k\), il \(k\) esimo numero armonico.
2.5 Best Response
Supponendo di giocare in modo ripetuto il GCG con una better response dynamic possiamo notare come una best response può essere calcolata in tempo polinomiale lavorando sul grafo \(G' = (V', E')\) ottenuto riscalando i pesi degli archi del grafo originale rispetto al profilo \(S_{-i}\).
In particolare l'arco \(e \in E'\) è scalato utilizzando il seguente peso
\[C_{e'} := \frac{C_e}{K_e(S_{-i}) + 1}\]
2.6 Bound on NE is NP-Hard
Andiamo adesso a dimostrare che il problema di limitare il costo di un NE per il GCG è un problema NP-Hard. In particolare vale il seguente
Teorema: Data una istanza del GCG e un valore \(c\), determinare se esiste un NE il cui costo è al più \(c\) è un problema NP-Hard.
Al fine di dimostrare tale risultato riportiamo una riduzione dal 3-dimensional matching problem
2.6.1 3D Matching Problem
Il 3-dimensional matching problem è così descritto
Input: Abbiamo tre insiemi disgiunti \(X, Y\) e \(Z\), ciascuno di cardinalità \(n \in \mathbb{N}\) e un insieme \(T \subseteq X \times Y \times Z\) di triple ordinate.
Domanda: Esiste un sottoinsieme di \(n\) triple in \(T\) tale che ciascun elemento di \(X \cup Y \cup Z\) è contenuto in una e una sola tripla?
2.6.2 Riduzione
Sia \(I\) una istanza del 3d matching problem, poniamo \(C := 3n\) e costruiamo la seguente istanza del gioco GCG
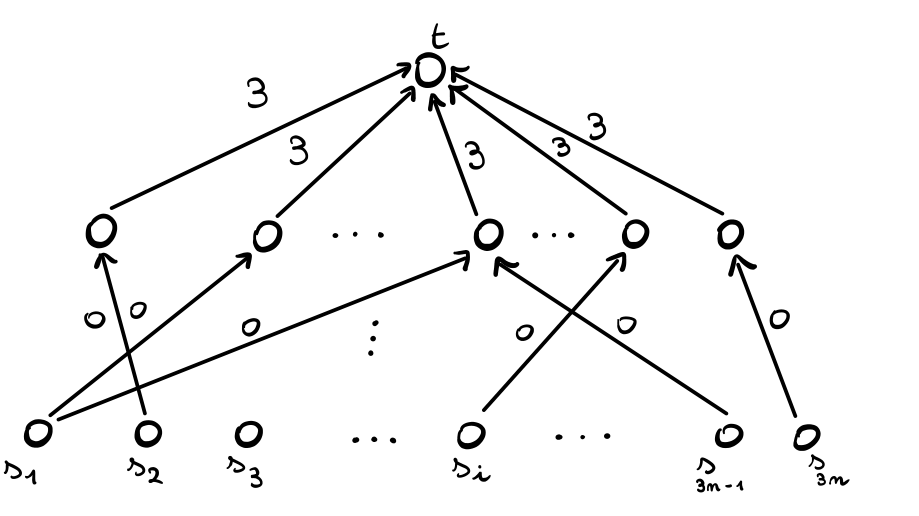
Il grafo è strutturato nel seguente modo
I nodi centrali sono associati alle triple in \(T\). In particolare per ogni tripla c'è un nodo;
I nodi in basso sono associati agli oggetti in \(X \cup Y \cup Z\). In particolare per ogni oggetto c'è un nodo.
Gli archi che collegano i nodi in basso a quelli al centro sono presenti se e solo se l'oggetto associato al nodo in basso è presente nella tripla associata al nodo al centro.
Dimostriamo adesso che esiste un 3d matching nell'istanza originale se e solo se esiste un NE di costo al più \(C = 3n\) nell'istanza del gioco GCG costruita.
\((\Rightarrow)\): Assumiamo che esiste un 3d matching e costruiamo un profilo \(S\) in cui ogni giocatore sceglie il path che passa al nodo al centro associato alla tripla presente nel matching.
Notiamo che \(\text{COST}(S) = 3n\) e inoltre che \(S\) è un NE, in quanto in \(S\) ciascun giocatore sta pagando \(1\), che è il costo minimo se si considera il fatto che il grado entrante dei nodi centrali è \(3\).
\[\tag*{$\checkmark$}\]
\((\Leftarrow)\): Supponiamo adesso che esiste un NE di costo \(\leq 3n\).
Iniziamo osservando che tale equilibrio sta utilizzando al più \(n\) archi di costo \(3\). Detto questo, osserviamo anche come l'equilibrio non può utilizzare meno di \(n\) archi di costo \(3\), in quanto abbiamo \(3n\) giocatori e ogni arco di costo \(3\) può essere utilizzato da al più \(3\) giocatori. Ma allora l'equilibrio sta utilizzando esattamente \(n\) archi di costo \(3\).
Ciascun arco di costo \(3\) poi definisce una particolare tripla, e messe assieme queste \(n\) triple riescono a coprire tutti i \(3n\) oggetti, risolvendo l'istanza del 3d matching problem.
\[\tag*{$\blacksquare$}\]
3 Potential Function Method
Iniziamo con una definizione
Def: Per ogni gioco finito, una exact potential function \(\Phi(\cdot)\) è una funzione che mappa ogni profilo di strategie \(S\) ad un numero reale tale che per ogni profilo \(S = (s_1, s_2, \ldots, s_k)\), se facciamo cambiare al giocatore \(i\) la sua strategia, ottenendo il nuovo profilo \(S' := (S_{-i}, s_{i}^{'})\), con \(s_i \neq s_{i}^{'}\), allora
\[\Phi(S) - \Phi(S') = \text{COST}_i(S) - \text{COST}_i(S')\]
Un gioco che possiede una funzione del genere è chiamato potential game.
Andiamo adesso a vedere una serie di risultati generali che valgono per ogni potential game.
3.1 Esistenza di un NE
Teorema 1: Ogni gioco potenziale ha almeno un puro NE, che è il profilo di strategie che minimizza la funzione \(\Phi(S)\).
Dimostrazione: Sia \(S\) il profilo di strategie che minimizza la funzione \(\Phi(\cdot)\), e consideriamo il profilo \(S'\) ottenuto dal profilo \(S\) facendo cambiare strategia al giocatore \(i\).
Dato che \(\Phi(S) \leq \Phi(S')\) otteniamo che
\[\text{COST}_i(S) - \text{COST}_i(S') = \Phi(S) - \Phi(S') \leq 0\]
il che implica \(\text{COST}_i(S) \leq \text{COST}_i(S')\), ovvero che al giocatore \(i\) non conviene quindi cambiare strategia, e quindi \(S\) è un NE.
\[\tag*{$\blacksquare$}\]
3.2 Convergenza della Better Response Dynamics
Teorema 2: In un qualsiasi potential game, la better response dynamics converge sempre ad un NE.
Dimostrazione: Utilizzando la better response dynamics è possibile passare da un profilo \(S\) ad un altro profilo \(S^{'}\) in modo tale da ridurre il costo per almeno un giocatore, diciamo il giocatore \(i\). In formula,
\[\text{COST}_i(S) \geq \text{COST}_i(S') \implies \Phi(S') \leq \Phi(S)\]
da questo segue che spostandoci di profilo in profilo tramite la better response dynamics stiamo essenzialmente simulando una ricerca locale del minimo di \(\Phi(S)\). Dato poi che abbiamo un numero finito di profili, ad un certo punto dobbiamo arrivare ad un minimo locale, che da quanto visto prima rappresenta proprio un NE.
\[\tag*{$\blacksquare$}\]
3.3 Upper Bound per PoS
Teorema 3: Se abbiamo un potential game con una potential function \(\Phi(\cdot)\) e esistono due valori, \(A, B \in \mathbb{R^+}\) tali che per ogni outcome \(S\) vale
\[\frac{\text{COST}(S)}{A} \leq \Phi(S) \leq B \cdot \text{COST}(S)\]
allora il PoS è al massimo \(A \cdot B\).
Dimostrazione: Sia \(S'\) il profilo che minimizza \(Phi\), e sia \(S^*\) il profilo che minimizza il costo sociale. Allora,
\[\begin{split} &\quad\quad \frac{\text{COST}(S')}{A} \leq \Phi(S') \leq \Phi(S^*) \leq \text{COST}(S^*) \cdot B \\ &\iff \frac{\text{COST}(S')}{\text{COST}(S^*)} \leq A \cdot B \\ &\iff \text{PoA} \leq \frac{\text{COST}(S')}{\text{COST}(S^*)} \leq A \cdot B \\ \end{split}\]
\[\tag*{$\blacksquare$}\]