AGT - 06 - Algorithmic Mechanism Design III
Lecture Info
Data:
Sito corso: AGT_2018
Slides: 06 - AMD III
Introduzione: In questa lezione abbiamo terminato la trattazione della progettazione di meccanismi discutendo il problema dell'asta combinatoria.
\(\require{cancel}\)
1 Combinatorial Auction
La combinatorial auction è una generalizzazione della single item auction affrontata in una lezione precedente.
In questa versione abbiamo più oggetti da vendere, e ogni agente vuole comprarne un particolare sottoinsieme. Il tipo dell'agente \(a_i\) è un valore \(t_i\) che intuitivamente rappresenta il valore massimo che l'agente è disposto a pagare per ottenere il proprio bundle di oggetti. Se \(a_i\) ottiene il suo bundle pagando \(p\), la sua utility è \(u_i = t_i - p\). Il nostro compito è quello di progettare un meccanismo che decide quale agente accontetare, e quanto i vari agenti dovranno pagare.
Formalmente,
Abbiamo \(n\) giocatori e \(m\) oggetti.
Ciascun giocatore \(a_i\) vuole un sottoinsieme \(S_i\) degli oggetti, e il tipo dell'agente è un numero \(t_i \in \mathbb{R}\), che rappresenta il valore complessivo degli oggetti in \(S_i\) secondo \(a_i\).
Un possibile outcome è un sottoinsieme \(W \subseteq \{1, \ldots, n\}\) tale che
\[\forall i, j \in W: \,\, i \neq j \implies S_i \cap S_j = \emptyset\]
Fissato un outcome \(w \in \mathcal{F}\), la valutazione di \(a_i\) per questo particolare output è data da
\[v_i(t_i, W) = \begin{cases} t_i \,\,&,\,\, i \in W \\ 0 \,\,&,\,\, \text{ altrimenti } \end{cases}\]
La social-choice function è definita come segue
\[f(t) := \underset{W \in \mathcal{F}}{\arg\max} \sum_{i \in W} t_i\]
Andiamo adesso a cercare un meccanismo truthful per risolvere questo problema.
1.1 VCG Mechanism
Per come abbiamo definito la SCF abbiamo che
\[f(t) := \underset{W \in \mathcal{F}}{\arg\max} \sum_{i \in W} t_i = \underset{W \in \mathcal{F}}{\arg\max} \sum_i v_i(t_i, W)\]
dunque il problema è un problema utilitario, e quindi possiamo utilizzare un meccanismo VCG della forma \(M = \langle g(r), p(x)\rangle\) con
L'algoritmo \(g(r)\) è definito come segue
\[g(r) = x^{*} := \underset{W \in \mathcal{F}}{\arg\max} \sum_j v_j(r_j, x)\]
L'agente \(a_i\) viene pagato nel seguente modo
\[p_i(x^*) := \sum_{j \neq i} v_j(r_j, g(r_{-i})) - \sum_{j \neq i} v_j(r_j, x^*)\]
1.1.1 Impossibility Result
Notiamo che per poter applicare questo meccanismo dobbiamo essere in grado di calcolare la soluzione ottima \(g(r)\) fissato il vettore \(r\). Questo, purtroppo, risulta essere un problema difficile, come mostra il seguente risultato.
Teorema 1: Approssimare CA con un fattore migliore di \(m^{\frac12 - \epsilon}\) è un problema NP-hard per ogni \(\epsilon > 0\).
per dimostrare questo teorema effettueremo una riduzione a partire da un problema famoso noto come indipendent set (IS). Per IS infatti vale il seguente risultato di impossibilità
Teorema 2: (J. Hastod, 2002): Approssimare IS con un fattore migliore di \(n^{1 - \epsilon}\) è un problema NP-Hard per ogni \(\epsilon > 0\) fissato.
Procediamo quindi con la dimostrazione del teorema 1.
dim: Andiamo a far vedere che \(\text{IS} \preceq \text{CA}\).
Consideriamo dunque una istanza \(I = \langle G=(V, E), k \rangle\in \text{IS}\), e costruiamo la relativa istanza \(I^{'} \in \text{CA}\) nel seguente modo:
Ogni arco in \(E\) diventa un oggetto in \(I^{'}\).
Ogni nodo in \(i \in V\) diventa un agente in \(I^{'}\), con
\(S_i := \{ \text{ insieme di oggetti associati ad archi incidenti ad } i\}\)
\(t_i := 1\)
Così facendo abbiamo che l'istanza \(I^{'}\) ha una soluzione di valore $ k$ se e solo se esiste un indipendent set di size \(\geq k\). Da questo segue che una soluzione di valore \(k\) per una istanza di \(\text{CA}\) con
\[\frac{\text{OPT}_{\text{CA}}}{k} \leq m^{\frac12 - \epsilon}\]
implicherebbe l'esistenza di una soluzione di valore \(k\) per l'istanza di \(\text{IS}\) con
\[\frac{\text{OPT}_{\text{IS}}}{k} = \frac{\text{OPT}_{\text{CA}}}{k} \leq m^{\frac12 - \epsilon} \leq n^{1 - 2 \epsilon}\]
In quanto \(m \leq n^2\) e quindi \(m^{\frac12 - \epsilon} \leq (n^2)^{\frac12 - \epsilon} = n^{1 - 2 \epsilon}\).
\[\tag*{$\blacksquare$}\]
1.2 OP Mechanism
Anche se il meccanismo VCG non è computabile in tempo polinomiale, notiamo che il problema CA è anche un problema ad un parametro. Più propriamente, è un problema di binary demand in quanto
Il tipo di \(a_i\) è un singolo parametro \(t_i \in \mathbb{R}\).
La valutazione di \(a_i\) dato un outcome \(W \in \mathcal{F}\) ha la seguente forma
\[v_i(t_i, w) = t_i \cdot w_i(w)\]
con
\[w_i(w) := \begin{cases} 1 \,\,&,\,\, i \in W \\ 0 \,\,&,\,\, \text{ altrimenti } \end{cases}\]
Dato che stiamo approcciando un problema di massimizzazione, è utile introdurre la seguente definizione.
Def. Un algoritmo \(g(\cdot)\) per un problema BD di massimizzazione è monotono se per ogni agente \(a_i\) e per ogni scelta fissata degli altri giocatori \(r_{-i} = (r_1, \ldots, r_{i-1}, r_{i+1}, \ldots, r_{N})\) il carico di lavoro del giocatore \(a_i\) ha la seguente forma
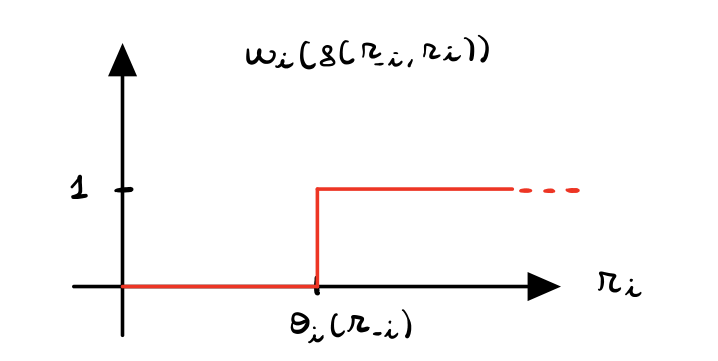
dove il valore \(\theta_i(r_{-i})\) è detto valore di soglia.
1.2.1 Greedy Algorithm
il nostro obiettivo è quindi quello di definire un meccanismo \(M = \langle g(r), p(x) \rangle\) tale che
L'algoritmo \(g(\cdot)\) è monotono e calcola una "buona" approsimzione della soluzione ottima.
Sia \(g(\cdot)\) che \(p(\cdot)\) sono calcolabili in tempo polinomiale.
A tale fine è possibile utilizzare il seguente algoritmo greedy per calcolare l'outcome.

Valgono quindi i seguenti risultati.
Lemma: L'algoritmo \(g()\) appena descritto è monotono.
dim: Per dimostrare questo risultato dobbiamo dimostrare che, fissato un agente \(a_i\) che viene selezionato da \(g()\), abbiamo che \(a_i\) viene comunque selezionato quando aumenta la sua proposta. Ma questo è garantito, in quanto considerando l'ordinamento effettuato dall'algoritmo all'inizio
\[\frac{v_1}{\sqrt{|S_1|}} \geq \ldots \geq \frac{v_i}{\sqrt{|S_i|}} \geq \ldots \frac{v_n}{\sqrt{|S_n|}}\]
abbiamo che aumentando il valore di \(v_i\), l'agente \(a_i\) potrebbe solo muoversi più a sinistra, riuscendo ad essere selezionato ancora più velocemente di prima.
\[\tag*{$\blacksquare$}\]
1.2.2 Computing Payments
Dato che abbiamo a che fare con un problema BD, il pagamento dell'agente \(a_i\) equivale al valore della soglia \(\theta_i(r_{-i})\) che determina il punto in cui \(a_i\) viene selezionato.
Per calcolare tale valore consideriamo l'ordinamento effettuato dal nostro algoritmo greedy andando però a rimuovere l'agente \(a_i\)
\[\frac{v_1}{\sqrt{|S_1|}} \geq \ldots \geq \cancel{\frac{v_i}{\sqrt{|S_i|}}} \geq \ldots \frac{v_n}{\sqrt{|S_n|}}\]
e utilizziamo l'algoritmo greedy per trovare il più piccolo indice \(j\) che viene selezionato e tale che \(S_j \cap S_i \neq \emptyset\). Allora il pagamento dell'agente \(a_i\) è così calcolato
\[p_i = \theta_i(r_{-i}) = \begin{cases} 0 \,\,&,\,\, j \text{ non esiste } \\ \displaystyle{v_j \cdot \frac{\sqrt{|S_i|}}{\sqrt{|S_j|}}} \,\,&,\,\, \text{ altrimenti } \\ \end{cases}\]
1.2.3 Approximation Result
Per concludere, dimostriamo che l'algoritmo \(g(\cdot)\) ritorna una approssimazione della soluzione ottima.
Lemma: Sia \(\text{OPT}\) una soluzione ottimale per il problema CA, e sia \(W\) la soluzione calcolata dall'algoritmo greedy. Allora
\[\sum_{i \in \text{OPT}} v_i \leq \sqrt{m} \cdot \sum_{i \in W} v_i\]
dim. Definiamo, per ogni \(i \in W\), il seguente insieme
\[\text{OPT}_i := \{j \in \text{OPT}: \,\, j \geq i \,\, \land S_j \cap S_i \neq \emptyset\}\]
Notiamo subito che
\[\bigcup\limits_{i \in W} \text{OPT}_i = \text{OPT}\]
Infatti, dato \(k \in \text{OPT}\), consideriamo l'indice \(h\) più piccolo tale che \(h \in W\) e \(S_h \cap S_k \neq \emptyset\). Notiamo che necessariamente \(h \geq k\), e quindi \(k \in \text{OPT}_h\). L'altro lato è dimostrato banalmente per definizione.
Ma allora, per dimostrare il nostro risultato, ci basta dimostrare che
\[\forall i \in W: \,\, \sum_{j \in \text{OPT}_i} v_j \leq \sqrt{m} \cdot v_i\]
infatti se fosse così, allora
\[\sum_{i \in \text{OPT}} v_i \leq \sum_{i \in W} \sum_{j \in \text{OPT}_i} v_j \leq \sum_{i \in W} \sqrt{m} \cdot v_i = \sqrt{m} \sum_{i \in W} v_i\]
Notiamo a questo punto che per come è stato definito il nostro algoritmo greedy abbiamo che per ogni \(j \in \text{OPT}_i\), vale
\[\frac{v_j}{\sqrt{|S_j|}} \leq \frac{v_i}{\sqrt{|S_i|}} \iff v_j \leq v_i \cdot \frac{\sqrt{|S_j|}}{\sqrt{|S_i|}}\]
Ma allora per ogni \(i \in W\)
\[\sum_{j \in \text{OPT}_i} v_j \leq \frac{v_i}{\sqrt{|S_i|}} \cdot \sum_{j \in \text{OPT}_i} \sqrt{|S_j|}\]
A questo punto è utile ricordare la Cauchy-Schwarz inequality, che ci dice che dati due vettori \(x = (x_1, \ldots, x_n)\) e \(y = (y_1, \ldots, y_n)\), vale che
\[\sum_{j = 1}^n x_j y_j \leq \Big(\sum_{j = 1}^n x_j^2 \Big)^{\frac12} \cdot \Big(\sum_{j = 1}^n y_j^2 \Big)^{\frac12}\]
Nel nostro caso particolare poniamo \(n := |\text{OPT}_i|\) e per ogni \(j = 1,...,n\) poniamo \(x_j := 1\) e \(y_j := \sqrt{|S_j|}\) per ottenere
\[\begin{split} \sum_{j = 1}^n \sqrt{|S_j|} = \sum_{j = 1}^n x_j y_j &\leq \Big(\sum_{j = 1}^n x_j^2 \Big)^{\frac12} \cdot \Big(\sum_{j = 1}^n y_j^2 \Big)^{\frac12} \\ &= \sqrt{|\text{OPT}_i|} \cdot \sqrt{\sum_{j = 1}^n |S_j|} \\ &\leq \sqrt{|S_i|} \cdot \sqrt{m} \\ \end{split}\]
In quanto abbiamo al massimo \(m\) oggetti, e quindi \(\sum_{j = 1}^m |S_j| \leq m\), e il numero di agenti in \(|\text{OPT}_i|\) non può superare \(|S_i|\), perché altrimenti ci sarebbero due agenti interessati allo stesso oggetto.
Mettendo tutto insieme otteniamo
\[\begin{split} \sum_{j \in \text{OPT}_i} v_j &\leq \frac{v_i}{\sqrt{|S_i|}} \cdot \sum_{j \in \text{OPT}_i} \sqrt{|S_j|} \\ &\leq \frac{v_i}{\sqrt{|S_i|}} \cdot \sqrt{|S_i|} \cdot \sqrt{m} \\ &= v_i \sqrt{m} \\ \end{split}\]
\[\tag*{$\blacksquare$}\]