AR - 08 - Reti di Informazioni II

Definiamo le seguenti quantità

• \(P_i^{(k)} := \text{ rank della pagina } i \text{ al tempo } k\)

• \(w_i := \text{ out-degree della pagina } i\)

Inizialmente il flusso viene distribuito in modo uniforme tra le pagine della rete, e quindi ogni pagina ha un flusso di \(1/n\). Al tempo \(k\) poi ciascuna pagina distribuisce in modo uniforme il proprio flusso a tutte le pagine adiacenti puntate dal nodo. Formalmente otteniamo quindi queste formule,

• \(\displaystyle{\forall i: \,\, P_i^{(0)} := \frac{1}{n}}\)

• \(\displaystyle{\forall k \geq 1 : \,\, P_i^{(k+1)} := \sum\limits_{\substack{j \to i}} \frac{P_j^{(k)}}{w_j}}\)

Volendo utilizzare una notizione matriciale, possiamo definire la seguente matrice

\[N_{i, j} = \begin{cases} \frac{1}{w_i} &\,\, , \text{ se } i \to j \\ 0 &\,\, , \text{ altrimenti} \end{cases}\]

per ottenere la seguente notazione sintetica

\[P^{(k+1)} := N^T \cdot P^{(k)}\]

Notiamo che la formulazione data però ha un grave problema nel modo in cui distribuisce il flusso. In particolare, se il grafo non è fortemente connesso, il flusso tenderà a convergere verso le componenti connesse che non hanno archi uscenti.

A seguire mostriamo un esempio per chiarire questa tendenza

• Iniziamo distribuendo in modo uniforme il flusso in tutti i nodi

  

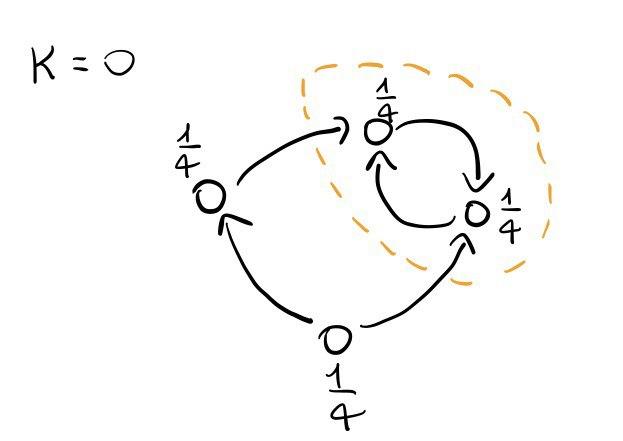
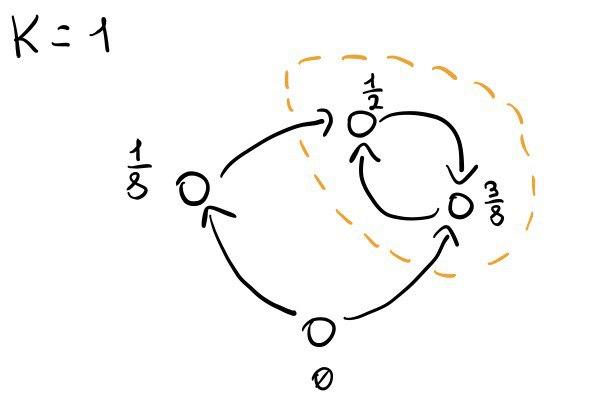
• Effettuiamo la prima re-distribuzione di flusso, in cui ciascun nodo passa il proprio flusso ai nodi adiacenti puntati da esso. Come possiamo vedere alla fine della re-distribuzione di flusso un nodo resta senza flusso, in quanto non è puntato da nessun altro nodo.

  

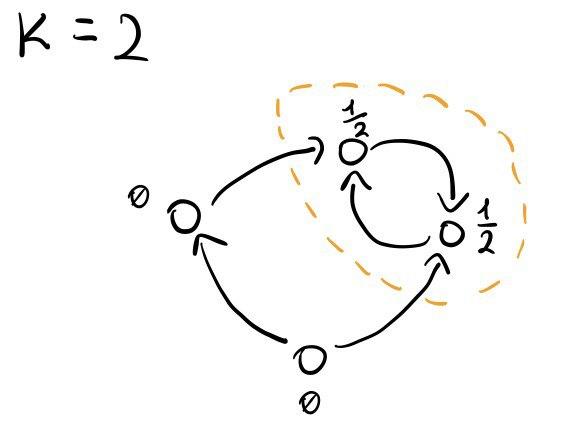
• Dopo due iterazioni l'intero flusso che era stato immesso nella rete si è concentrato nella componente connessa tratteggiata. Questo è proprio conseguenza del fatto che tale componente connessa non ha archi uscenti a nodi che non fanno parte della componente connessa.

  

Per risolvere il problema della re-distribuzione del flusso appena visto, l'idea è quella di modificare la formulazione base descritta per permettere ad una determinata quantità di flusso di essere redistribuita tra tutti i nodi della rete, senza nessun tipo di vincolo.

Tale formulazione prende il nome di Scaled Page Rank, ed è formalizzata come segue: si fissa un valore reale \(s \in (0, 1)\), e si modificano le formule riportate prima nel seguente modo

• \(\displaystyle{\forall i: \,\, SP_i^{(0)} := \frac{1}{n}}\)

• \(\displaystyle{\forall k \geq 1 : \,\, P_i^{(k+1)} := \underbrace{s \cdot \sum\limits_{\substack{j \to i}} \frac{P_j^{(k)}}{w_j}}_{\text{fluido ricevuto} \\ \text{dai propri vicini}} + \underbrace{(1 - s) \cdot \sum_{j = 1}^n \frac{SP_j^{(k)}}{n}}_{\text{fluido re-distribuito} \\ \text{da tutti i nodi}}}\)

Notiamo poi che SPR è un metodo conservativo per distribuire il fluido, e infatti si può dimostrare per induzione che ad ogni tempo \(k\) la somma del fluido di tutte le pagine vale sempre \(1\), ovvero che \(\forall k: \,\, \sum_{i = 1}^n SP_i^{(k+1)} = 1\). Da questo segue che

\[\displaystyle{P_i^{(k+1)} = s \cdot \sum\limits_{\substack{j \to i}} \frac{P_j^{(k)}}{w_j} + \frac{1-s}{n}}\]

Volendo nuovamente utilizzare una notazione matriciale, possiamo definire la seguente matrice

\[\overline{N}_{i, j} = \begin{cases} s \cdot \frac{1}{w_j} + (1 - s) \cdot \frac{1}{n} & \,\, , i \to j \\ (1 - s) \cdot \frac{1}{n} & \,\, , i \not \to j \\ \end{cases}\]

per ottenere la seguente notazione sintetica

\[SP^{(k+1)} = \overline{N}^T \cdot SP^{(k)}\]

Il seguente teorema sarà di fondamentale importanza per ottenere la convergenza dello Scaled Page Rank (SPR).

Teorema: Sia \(A\) una matrice \(n \times n\) a valori reali, tale che \(\forall i, j: A_{i,j} > 0\). Allora valgono le seguenti cose

1. \(\exists \,\, c\) autovalore di \(A\) tale che

   \[\forall c' \text{ autovalore di } A: c' \neq c \implies c > |c'|\]

2. \(\exists! y \in \mathbb{R}^n\) autovettore di \(A\) associato all'autovalore \(c\), con \(y\) tutto positivo.

3. Se \(c = 1\), allora

   \[\forall SP^{(0)} \geq 0: \,\, \lim_{k \to \infty} SP^{(k)} = \alpha \cdot y \,\,\,, \alpha \neq 0\]

La convergenza del metodo Scaled Page Rank è ottenuta utilizzando il teorema di Perron-Frobenius appena enunciato, e notando che \(\overline{N}^T\) è una matrice stocastica, ovvero una matrice in cui la somma degli elementi in ogni colonna (o in ogni riga) è \(1\).

Dato che \(\overline{N}^T\) è una matrice stocastica, ne segue che l'autovalore massimo è \(1\). Possiamo quindi applicare il teorema di Perron-Frobenius per ottenere la convergenza desiderata.

Notiamo che possiamo interpretare il page rank come una random walk su un grafo orientato.

La distribuzione uniforme del flusso che viene fatta inizialmente quindi è interpretata come una scelta random di iniziare da un qualsiasi nodo del grafo con probabilità uniforme.

La re-distribuzione del flusso che invece viene effettuata nelle varie iterazioni del page rank invece può essere interpretata come la probabilità di scegliere un link a caso in modo uniforme nella pagina in cui mi trovo per andare in una nuova pagina.

Infine, la re-distribuzione che viene fatta su tutti i nodi della rete infine corrisponde alla scelta, che può essere fatta in ogni momento, di iniziare la nostra random walk da capo iniziando da qualsiasi pagina della rete.