AR - 12 - Processi di Diffusione I
Lecture Info
Data:
Capitolo Libro: Chapter 19 - Cascading Behavior in Networks
Introduzione: In questa lezione scendiamo di livello ed analizziamo l'influenza che la topologia della rete ha rispetto alle scelte compiute dai singoli individui. In particolare introduciamo lo studio dei processi di diffusione delle innovazioni (che possono essere tecnologiche o culturali) tramite un modello basato su un semplice Network Coordination Game e verifichiamo le condizioni necessari e sufficienti affinché una innovazione sia in grado di propagarsi all'interno di una rete sociale. Terminiamo la lezione introducendo il concetto di Azione Collettiva.
1 Diffusione delle Innovazioni
Al fine di definire un modello in grado di catturare il modo in cui le innovazioni si propagano in una rete è fondamentale iniziare facendo riferimento alla letteratura, e in particolare ad una serie di studi empirici relativi a questo argomento.
Tra tutti i risultati empirici ottenuti, due studi in particolare risultano essere molto significativi:
Il paper di Ryan e Gross, "Acceptance and Diffusione of Hybrid Corn Seed in Two Iowa Communities", in cui è stato analizzato il processo di diffusione di un nuovo seme di mais all'interno di una comunità di agricoltori.
Il paper di Katz e Menzel, Medical Innovations: A Diffusion Study, in cui si è analizzato il processo di diffusione delle tetracicline, che sono dei particolari farmaci antibatterici, da parte dei medici negli Stati Uniti.
Posto che i due studi in questione fanno riferimento a diverse comunità e a diverse innovazioni, condividono comunque una serie di tratti comuni, di cui vale la pena discuterne. Questi sono,
In entrambi i casi l'iniziale ignoranza rispetto alla particolare innovazione presa in considerazione ha comportato un determinato fattore di rischio agli adottanti iniziali. Alla fine però il beneficio derivante dall'utilizzo dell'innovazione ha permesso all'innovazione di diffondersi nella rete.
In entrambi i casi gli adottanti iniziali erano persone tipicamente con uno status socio-economico più elevato e con una tendenza a viaggiare molto.
In entrambi i casi le decisioni e le eventuali adozioni della nuova innovazione venivano eseguite nel contesto di una struttura sociale in cui le persone potevano osservare i propri vicini, amici e colleghi.
Col passare del tempo alcuni ricercatori hanno comincinato ad identificare alcune delle principali caratteristiche che favorivano, o sfavorivano, la diffusione di una innovazione all'interno di una rete sociale. Di particolare interesse troviamo il libro di Everett Rogers, "Diffusion of Innovations". Everett ha cercato di formalizzare in una serie di principi le possibili ragioni che potevano portare una innovazione a non diffondersi in una rete anche quando era significativamente migliore rispetto alle tecnologie o pratiche già esistenti.
Everett afferma che il successo di una innovazione dipende almeno dai seguenti fattori:
La complessità, per permettere alle persone di poterla capire ed utilizzare.
L'osservabilità, per permettere alle altre persone di capire che le persone stanno utilizzando quella particolare innovazione.
La compatibilità rispetto al sistema sociale in cui l'innovazione vuole entrare.
In particolare si è visto come il concetto di omofilia presente nelle reti sociali, ovvero la tendenza delle persone di avvicinarsi a persone simili e a diventare più simili ai propri vicini col passare del tempo, può agire come una barriera rispetto alla diffusione di nuove innovazioni. Detto altrimenti, può risultare difficile ad una innovazione di entrare e diffondersi all'interno di comunità molto strette e compatte.
Andiamo adesso ad introdurre un modello formale per analizzare questo fenomeno.
2 Network Coordination Game
Al fine di modellare un processo di diffusione all'interno di una rete possiamo utilizzare un coordination game. Il gioco a cui siamo interessati può essere descritto dalla seguente matrice
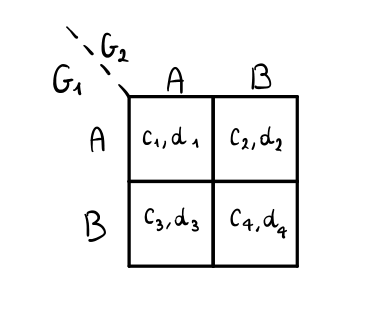
ed è composto dai seguenti elementi:
\(G_1\), \(G_2\), gicatori.
\(A\) e \(B\) mosse mutualmente esclusive.
\(c_1\) guadagno di \(G_1\) se \(G_1\) sceglie \(A\) e \(G_2\) sceglie \(B\).
\(d_1\) guadagno di \(G_2\) se \(G_1\) sceglie \(A\) e \(G_2\) sceglie \(B\).
...
\(d_4\) guadagno di \(G_2\) se \(G_1\) sceglie \(B\) e \(G_2\) sceglie \(B\).
Nel nostro caso particolare possiamo supporre di modellare una situazione simile a quella descritta dal paper di Ryan e Gross: Abbiamo una comunità di agricoltori. Inizialmente tutti gli agricoltori utilizzano tutti il vecchio seme (scelta \(B\)). Ad un certo punto si regala il nuovo seme (scelta \(A\)) ad una serie di agricoltori. Siamo quindi interessati a capire il processi di diffusione del nuovo seme nella rete.
Supponiamo poi che il guadagno di un agricoltore dipende da quanti agricoltori a lui adiacenti utilizzano lo stesso seme. In particolare consideriamo che \(G_1\) rappresenti un agricoltore che deve ancora adottare il nuovo seme, mentre \(G_2\) lo ha già adottato. Troviamo quindi il seguente gioco
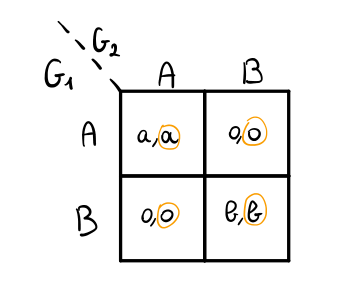
In altre parole, due agricoltori \(G_1\) e \(G_2\) possono guadagnare tra loro solamente se piantano lo stesso seme. In questo contesto quindi \(a\) rappresenta il guadagno ottenuto piantando il nuovo seme, mentre \(b\) rappresenta il guadagno ottenuto piantando il vecchio seme. Se i due agricoltori piantano semi diversi, allora nessuno guadagna nulla.
Notiamo poi che non ci interessa tanto il guadagno del giocatore $G_2, che è il giocatore che ha già scelto di utilizzare il nuovo seme. Siamo infatti solamente interessati a vedere se nuovi potenziali agricoltori scelgono di passare dal vecchio seme (scelta \(B\)), al nuovo seme (scelta \(A\)).
Il gioco appena introdotto considera le interazioni solamente tra una coppia di agricoltori. Fissato un agricoltore \(u \in V\) che utilizza il vecchio seme, abbiamo che \(u\) avrà più di un vicino, e per ogni vicino viene giocato lo stesso gioco appena descritto. Per capire se \(u\) sarà vantaggiato a cambiare scelta definiamo la seguente quantità
\[p := \text{ frazione dei vicini di } u \text{ che hanno scelto } A\]
Segue quindi che \(u\) cambierà seme quando
\[p \cdot a \geq (1 - p) \cdot b \iff p \geq \frac{b}{a+b} =: q\]
Il valore \(q\) è detto turning point. Notiamo che,
Se \(q\) è piccolo, allora \(a >> b\), e quindi bastano pochi vicini che scelgono \(A\) per far adottare \(A\).
Se \(q\) è grande invece abbiamo bisogno di tanti vicini per far adottare \(A\).
La dinamica da analizzare è quindi la seguente: consideriamo una rete in cui inizialmente tutti effettuano la scelta \(B\). Inizialmente facciamo convertire un numero ristretto di nodi, chiamati initiators, alla scelta \(A\) e vediamo quando otteniamo una situazione di equilibrio in cui a nessun nodo conviene cambiare scelta.
Notiamo che la natura della dinamica appena descritta può ottenere i tre seguenti tipi di equilibri:
Tutti i nodi scelgono \(B\). Questo caso è però da escludere se scegliamo almeno un initiator.
Tutti i nodi scelgono \(A\). In questo caso abbiamo che la scelta \(A\) riesce a diffondersi completamente, iniziando una cascata comportamentale.
Non tutti i nodi scelgono \(A\), ma \(A\) smette di diffondersi. In questo caso \(A\) si diffonde nella rete, ma non è in grado di iniziare una cascata comportamentale.
2.1 Esempio Diffusione
A seguire è riportato un esempio di diffusione in una rete quando \(a = 3\), \(b = 2\), e dunque \(q = 2/5\). I nodi bianchi sono i nodi di tipo \(B\), mentre quelli rossi sono i nodi di tipo \(A\). Inizialmente sono stati scelti due initiators per diffondere \(A\) nel resto della rete.
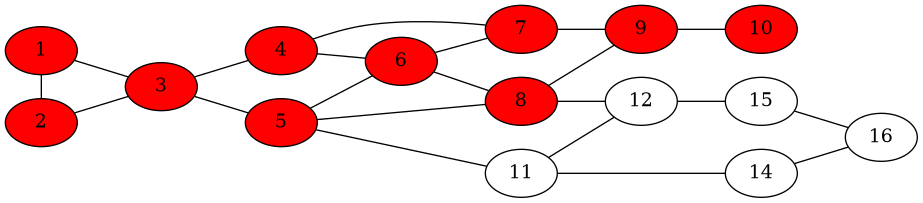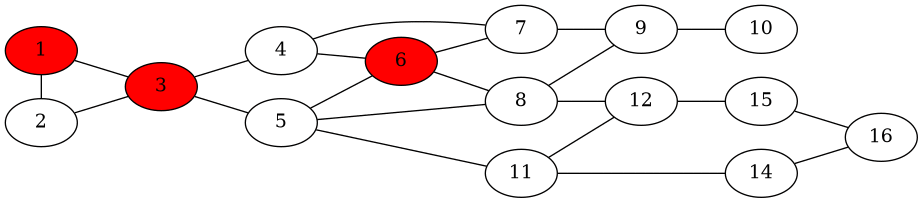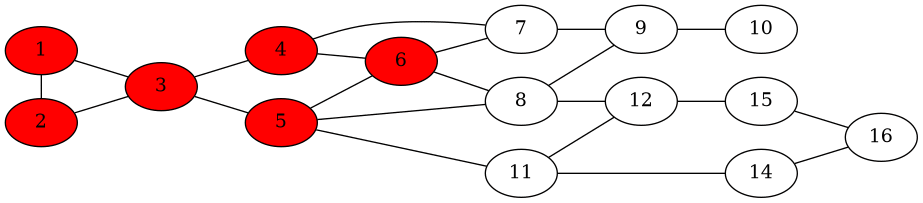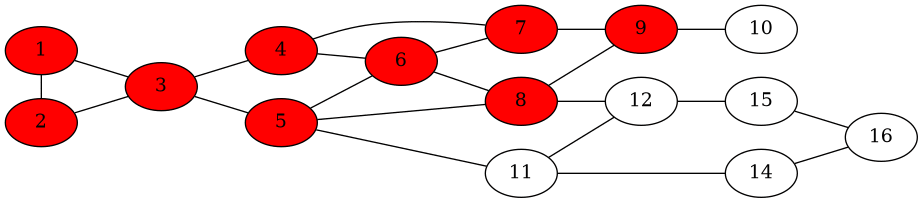
Notiamo come la diffusione inizia ma poi si ferma, non riuscendo a far partire una cascata e dunque non riuscendo ad infettare l'intera rete.
Una volta che abbiamo trovato un equilibrio del genere, per cercare di continuare a far diffondere \(A\) nella rete abbiamo due possibili scelte:
Possiamo dare il prodotto "gratis" ad altre persone, andando ad aumentare la presenza di nodi \(A\) in modo da convincere più persone a passare ad \(A\).
Possiamo "migliorare" il prodotto \(A\) andando quindi ad incrementare il valore \(a\). Infatti, più alto è il guadagno \(a\) e meno vicini mi servono per passare ad \(A\).
2.2 Problemi di Interesse
Nel contesto dei processi di diffusione in una rete sociale, abbiamo due classi di problemi interessanti, che sono:
Fissato il numero di initiators, siamo interessati a massimizzare la porzione di rete raggiunta.
Volendo raggiungere tutta la rete, voglio minimizzare il numero di initiators utilizzati.
Dato che queste domande fanno riferimento a problemi di ricerca moderna e dunque necessitano di strumenti fin troppo complessi per i nostri interessi, noi ci occuperemo non di questi problemi, ma cercheremo invece di rispondere alle seguenti domande
Come scegliamo gli initiators?
Qual'è il massimo valore di \(q\) che si serve per coprire la rete?
3 Clusters e Cascate
Nella descrizione iniziale avevamo menzionato il fatto che l'omofilia può agire come una naturale barriera alla diffusione di innovazioni. Andiamo adesso a formalizzare meglio questo concetto. A tale fine introduciamo la seguente definizione.
Def: Un sottoinsieme di vertici \(V' \subseteq V\) è detto cluster di densità \(p\) se
\[\displaystyle{\forall u \in V': \frac{|N(u) \cap V'|}{|N(u)|} > p}\]
Dunque \(V'\) è un cluster di densità \(p\) se ogni nodo in \(V'\) ha una frazione > \(p\) di vicini contenuti anche loro in \(V'\). Notiamo come la definizione appena data è una generalizzazione del concetto di web-communities, discusso in una lezione precedente.
Lo scopo di questa sezione sarà quello di dimostrare che i concetti di clusters e di cascata sono opposti tra loro: non possiamo avere cascate in presenza di determinati clusters, e viceversa la presenza di determinati clusters blocca la diffusione di cascate.
Sia \(G = (V, E)\). Inizialmente tutti i nodi sono di tipo \(B\). Ad un certo punto definiamo
\(V_0 := \text{ nodi che all'istante } 0 \text{ ricevono il prodotto } A\)
\(E_0 := \text{ archi che collegano nodi in } V - V_0\)
\(G_0 := (V - V_0, E_0)\)
In modo analogo definiamo
\(V_1, V_2, ..., V_t, \ldots\)
\(G_1 = (V - (V_0 \cup V_1), E_1)\)
\(G_2 = (V - (V_0 \cup V_1 \cup V_2), E_2)\)
\(\ldots\)
\(G_t = (V - (\cup_{i = 0}^t V_i), E_t)\)
Siamo ora in grado di dimostrare il seguente teorema.
Teorema: Dati \(G, V_0\) e \(q\), vale che
\[\bigcup\limits_{t \geq 0} V_t = V \iff G_0 \text{ non contiene clusters di densità } 1 - q\]
Notiamo che la condizione \(\cup_{t \geq 0} V_t = V\) equivale a dire che si genera una cascata completa, e quindi che \(A\) riesce a diffondersi completamente nella rete. Il teorema ci sta quindi dicendo che se vogliamo far iniziare una cascata, dobbiamo scegliere almeno un initiator per ogni cluster di densità \(1-q\), in quanto dall'esterno non siamo in grado di far diffondere \(A\) all'interno di questi clusters.
Dimostrazione:
\((\Rightarrow)\) Supponiamo che la cascata inizia, ovvero che \(\cup_{t \geq 0} V_t = V\).
In questa parte della dimostrazione vogliamo far vedere che i cluster di densità \(1-q\) rappresentano dei blocchi per la diffusione della cascata. Dunque, se la cascata si diffonde, necessariamente non esistono clusters di densità \(1-q\).
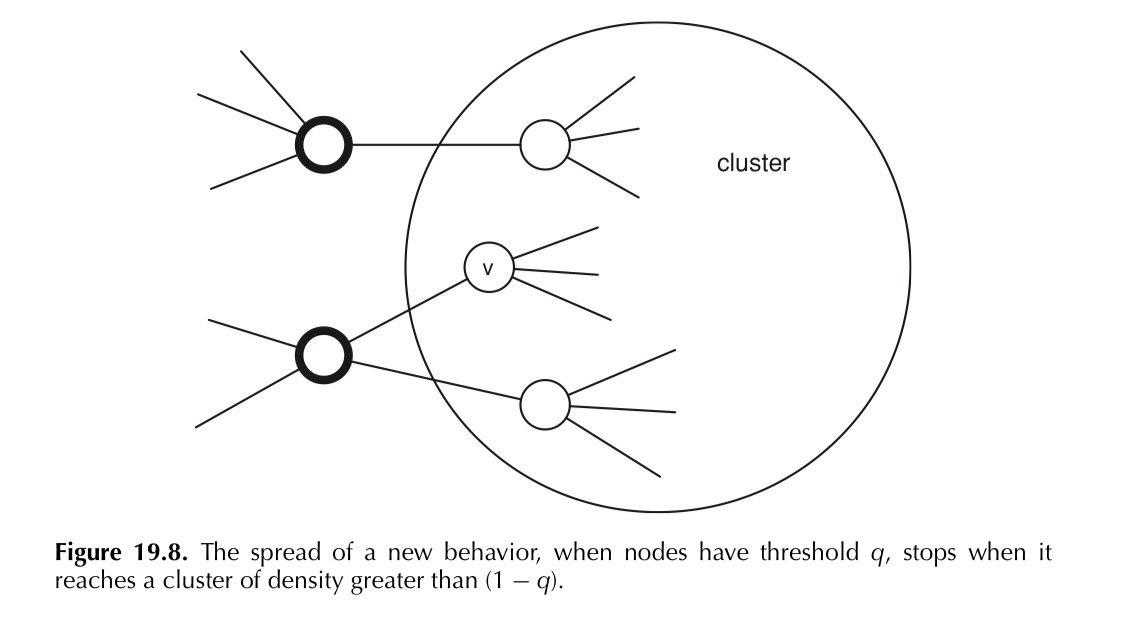
A tale fine supponiamo, per assurdo, che esiste un \(C \in V - V_0\) tale che \(C\) è un cluster di densità \(1-q\).
Dato che si genera una cascata, deve esistere un nodo \(u \in C\) che adotterà per primo, tra tutti i nodi in \(C\), la nuova scelta \(A\). Supponiamo che l'istante in cui \(u\) adotta il nuovo prodotto \(A\) sia \(\bar{t}\). Da questo segue che
\(C \cap (V_0 \cup V_1 \cup \ldots \cup V_{\bar{t} - 1}) = \emptyset\)
\(C \cap V_{\bar{t} - 1} \neq \emptyset\)
Notiamo a questo punto che
Dato che \(u\) è infettato al tempo \(\bar{t}\), abbiamo che al tempo \(\bar{t} - 1\) la frazione di vicini di \(u\) che hanno già scelto \(A\) è \(\geq q\). In formula,
\[\frac{| N(u) \bigcap (\bigcup\limits_{t = 0}^{\bar{t} - 1} V_t)|}{|N(u)|} \geq q\]
Dato che \(C \subseteq V - \cup_{t = 1}^{\bar{t}-1} V_t\), e che \(C\) è un cluster di densità \(1-q\), abbiamo che
\[\frac{| N(u) \bigcap (V - \bigcup\limits_{t = 0}^{\bar{t} - 1} V_t)|}{|N(u)|} \geq \frac{|N(u) \cap C|}{|N(u)|} > 1 - q\]
Possiamo esprimere \(1\) nel seguente modo
\[\begin{split} &1 = \frac{|N(u)|}{|N(u)|} \\ &= \frac{\bigg|\bigg[ N(u) \bigcap (V - \bigcup\limits_{t = 0}^{\bar{t} - 1} V_t) \bigg] \bigcup \bigg[ N(u) \bigcap (\bigcup\limits_{t = 0}^{\bar{t} - 1} V_t \bigg] \bigg|}{|N(u)|} \\ &= \frac{\bigg |\bigg[ N(u) \bigcap (V - \bigcup\limits_{t = 0}^{\bar{t} - 1} V_t) \bigg] \bigg| + \bigg| \bigg[ N(u) \bigcap (\bigcup\limits_{t = 0}^{\bar{t} - 1} V_t \bigg] \bigg|}{|N(u)|} \\ \end{split}\]
Mettendo i tre punti assieme otteniamo
\[\begin{split} &1 = \frac{\bigg |\bigg[ N(u) \bigcap (V - \bigcup\limits_{t = 0}^{\bar{t} - 1} V_t) \bigg] \bigg| + \bigg| \bigg[ N(u) \bigcap (\bigcup\limits_{t = 0}^{\bar{t} - 1} V_t \bigg] \bigg|}{|N(u)|} \\ &\iff \frac{\bigg| N(u) \bigcap (\bigcup\limits_{t = 0}^{\bar{t} - 1} V_t ) \bigg|}{|N(u)|} = 1 - \frac{\bigg| N(u) \bigcap (V - \bigcup\limits_{t = 0}^{\bar{t} - 1} V_t) \bigg|}{|N(u)|} \\ \end{split}\]
Infine, dall'ultima equazione troviamo
\[\frac{\bigg| N(u) \bigcap (\bigcup\limits_{t = 0}^{\bar{t} - 1} V_t ) \bigg|}{|N(u)|} = 1 - \frac{\bigg| N(u) \bigcap (V - \bigcup\limits_{t = 0}^{\bar{t} - 1} V_t) \bigg|}{|N(u)|} < 1 - (1 - q) = q\]
che entra in contraddizione con il fatto che il nodo \(u\) è stato contagiato al tempo \(\bar{t}\). Concludiamo quindi osservando che se la cascata parte, allora non possono esistere cluster di densità \(1-q\).
\((\Leftarrow)\) Supponiamo \(\cup_{t \geq 0} V_t \subset V\), ovvero che la cascata non parte e ci sono dei nodi che continuano a scegliere \(B\). In questa parte della dimostrazione facciamo vedere che l'unico blocco possibile che una cascata può incontrare è proprio un cluster di densità \(1-q\). Quindi, se la cascata si blocca, esiste necessariamente un cluster di densità \(1-q\) che non è stato contagiato.
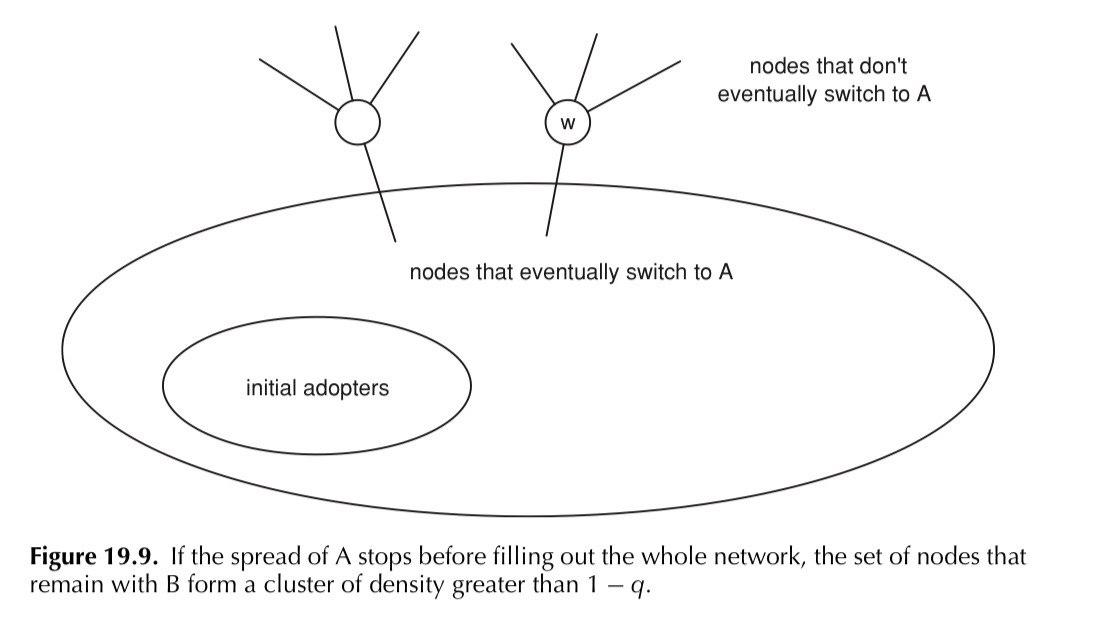
In particolare sia \(V' := V - \cup_{t \geq 0} V_t\). Dalle ipotesi sappiamo che \(V' \neq \emptyset\). Sia quindi \(u \in V'\). Dato che \(u\) non è stato contagiato, sappiamo che
\[\frac{|N(u) \cap (\cup_{t \geq 0} V_t)|}{|N(u)|} < q\]
Ma allora vale
\[\frac{|N(u) \cap (V - \cup_{t \geq 0} V_t)|}{|N(u)|} > 1 - q\]
in quanto la somma tra le due quantità è \(1\). Dato che questo value per ogni \(u \in V'\), ne segue che \(V'\) è un cluster di densità \(1-q\).
\[\tag*{$\blacksquare$}\]
3.1 Osservazioni Finali
Segue qualche osservazione
Trovare un buon insieme di initiators è un problema NP-completo.
I weak-ties sono utili dal punto di vista informativo, ma sono deboli per la diffusione di innovazioni.
Per rendere il modello più reale possiamo introdurre dei guadagni particolari ai vari nodi della rete. Formalmente introduciamo le seguenti quantità,
\[\begin{split} \forall v \in V: \,\,\,\,\, &a_v := \text{guadagno del nodo } v \text{ per la scelta } A\\ &b_v := \text{guadagno del nodo } v \text{ per la scelta } B\\ \end{split}\]
Il turn-over point diventa quindi specifico per il singolo nodo. In particulare il nodo \(v\) sceglie di cambiare scelta e passare ad \(A\) se, definita con \(p_v\) la frazione dei vicini di \(v\) che hanno scelto \(A\), si ha che
\[p_v \geq \frac{b_v}{a_v + b_v} =: q_v\]
In questo modello più complesso il concetto di cluster di densità \(q\) non può più essere utilizzato. Si introduce quindi il concetto di blocking cluster, definito come segue
\[C \subseteq V: \,\, \forall v \in C \,\,\, \frac{|N(u) \cap C|}{|N(u)|} > 1 - q_v\]
4 Azione Collettiva
Consideriamo una azione a cui si aderisce solamente se c'è una minimia soglia di presenza. Formalmente per ogni nodo \(v \in V\) si definisce
\[k_v := \text{soglia di sicurezza di v }\]
Questo significa che per partecipare \(v\) deve sapere che almeno altri \(k_{v}-1\) nodi parteciperanno.
4.1 Esempi
Consideriamo una serie di grafi e di soglie di sicurezza, e vediamo se si è in grado di far partire una azione collettiva.
Esempio 1: In questo grafo non parte, in quanto nessun nodo aderisce.
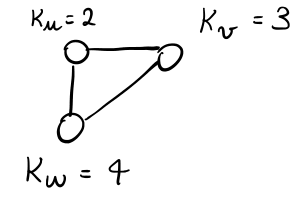
Esempio 2: Non parte, in quanto ogni nodo vede solamente i propri vicini.
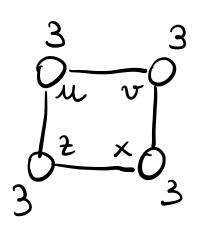
Esempio 3: Parte all'interno del triangolo.
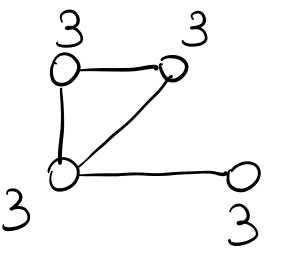
Questi esempi fanno capire il perché i regimi totalitary puntano a danneggiare e screditare i mezzi di informazione al fine di rendere difficile la cooperazione.
Consideriamo la TV. Notiamo che la TV non ci dà solo delle informazioni esplicite. La TV ci da anche l'informazione implicita che anche le altre persone stanno vedendo le stesse cose, e quindi che anche gli altro sanno le stesse cose. Sapere che gli altri sanno è una informazione molto importante.