AR - 13 - Processi di Diffusione II

Lecture Info

Data: [2018-11-28 mer]
Capitolo Libro: Chapter 19 - Cascading Behavior in Networks
Introduzione: In questa lezione abbiamo continuato la discussione sui processi di diffusione. In particolare abbiamo analizzato la diffusione di una nuova tecnologia all'interno di una rete sociale in funzione del valore del turning point $q$. Come risultato significativo abbiamo dimostrato un teorema che dice che per poter innescare una cascata, il turning point deve almeno essere $1/2$, e quindi che la nuova tecnologia, per poter essere adottata dall'intera rete, deve essere almeno buona quanto quella vecchia.

1 Turning Point

Dando per noto il modello introdotto nella scorsa lezione ricordiamo solamente che la diffusione della nuova tecnologia $A$ è regolata dal parametro $q$, definito come segue

\[q := \frac{b}{a + b}\]

Fissato $b$, più $a$ cresce e più $q$ diventa piccolo. Se sappiamo che per un certo valore $q_0$ la nuova tecnologia si diffonde completamente nell'intera rete, allora sappiamo anche quanto $A$ deve essere migliore di $B$, ovvero quanto $a$ deve essere più grande di $b$ per riuscire ad innescare una cascata comportamentale.

Noi siamo interessati a diffondere la nuova tecnologia $a$, cercando però di mantenere determinati costi sotto controllo. Questo si traduce dicendo che siamo interessati a valori alti di $q$ che riescano a far partire una cascata. Infatti, più alto è il valore di $q$, e meno dovrò investire nella nuova tecnologia $a$, riuscendo comunque a farla adottare da tutti gli individui della rete.

Siamo quindi interessati a studiare l'andamento della diffusione della nuova tecnologia in funzione di $q$, per vedere quanto possiamo aumentare il costo di $a$ riuscendo comunque a diffonderlo.

2 Capacità di Cascata

Per effettuare queste analisi consideriamo reti il cui numero di nodi è potenzialmente infinito. Un modo alternativo per dire la stessa cosa è che le reti con cui lavoriamo sono reti fissate con un numero arbitrario di punti, di cui noi però ne vediamo inizialmente solo la parte "centrale". Gli initiators vengono quindi pescati in questa parte "centrale", e dopo che sono stati scelti la rete comincia ad espandersi, e cominciamo a vedere anche le parti più "periferiche" della rete.

Questa scelta di trattare reti con un numero di nodi potenzialmente infinito è fatta per le seguenti ragioni

Come prima cosa, trattare reti con un numero arbitrario di nodi ci permette di togliere la dipendenza di $q$ dal parametro che regola il numero di nodi.
In reti con un numero di nodi finito possiamo sempre spingere il prodotto su tutti i nodi ponendo $a = +\infty$ in modo da ottenere $q=0$.

Dato $G = (V, E)$ con "$|V| \to \infty$", vogliamo trovare un insieme di initiators $V_0$ finito e di dimensione costante per riuscire a diffondere la nuova tecnologia in tutta la rete. Iniziamo quindi analizzando due particolari topologie.

2.1 Diffusione nel Cammino

Consideriamo un grafo $G$ che forma un semplice cammino come riportato dal seguente esempio

Prendiamo un qualsiasi nodo come initiator. Non ci interessa quale nodo prendiamo, data l'elevata simmetria del cammino. Notiamo che inizialmente solo i nodi adiacenti all'initiator si potranno "infettare", ovvero potranno cambiare alla nuova tecnologia $A$. Per infettarsi poi il turning point deve essere $\leq 1/2$. Dato che noi vogliamo valori del turning point alti, poniamo $q_1 = 1/2$ per ottenere la seguente dinamica

Abbiamo quindi fatto vedere che, se $|V_0| = 1$, allora $q_1 = 1/2$. Dire che $q_1 = 1/2$ poi significa dire che $a = b$, ovvero che in termine di qualità, $a$ è equivalente a $b$.

Anche andando ad aggiungere più di un initiators, la situazione non cambia molto, in quanto a sinistra o a destra di qualche initiators necessitiamo comunque che il turning point sia $\leq 1/2$, e quindi $q_2 = 1/2$ è il più alto turning point che possiamo ottenere.

In generale quindi abbiamo visto che nel cammino per ogni insieme di initiators $V_0$ di dimensione costante, vale sempre che il miglior $q$ che possiamo ottenere è proprio $q = 1/2$. Notiamo poi che il valore di $q$ trovato dipende solamente dalla topologia della rete. Per questa ragione si parla di capacità di cascata delle reti.

2.2 Diffusione nella Griglia

Consideriano adesso un grafo $G$ che forma la seguente topologia a griglia con delle diagonali

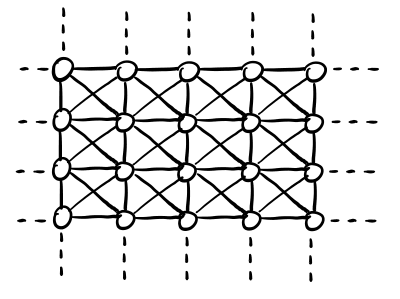
Iniziamo con un initiator, $|V_0| = 1$. Dato che ogni nodo ha $8$ vicini, per poter convincere i vicini del nostro initiator ad adottare la nuova tecnologia necessitiamo che $q_1 = 1/8$. Con questo valore di $q$ otteniamo infatti la seguente dinamica

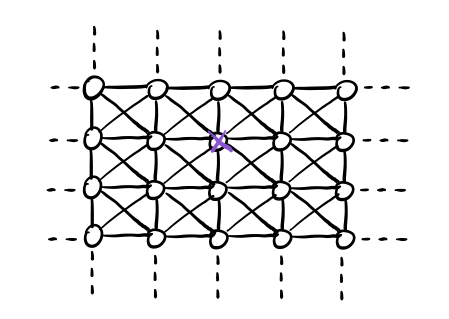
Notiamo però che il valore $q=1/8=0.125$ è abbastanza basso, e quindi $a$ deve essere abbastanza più alto di $b$ per potersi diffondere. Al fine di aumentare il turning point possiamo provare ad utilizzare più initiators.

Se utilizziamo due nodi come initiators, ovvero $|V_0| = 2$ tali che i due nodi condividano almeno un altro nodo, abbiamo che il più alto valore di $q$ sufficiente a far partire la cascata è $q_2 = 1/4$. La dinamica in questo caso è infatti la seguente

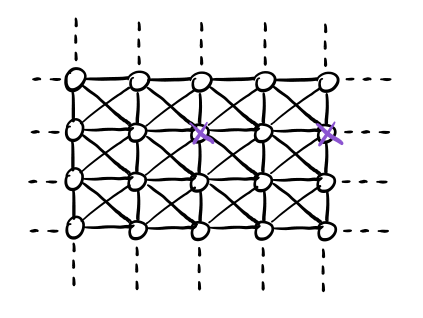
Utilizzando tre nodi come initiators il valore massimo di $q$ per far partire una cascata dipende da come questi nodi sono disposti. In particolare,

Se i tre initiators sono in fila, allora $q_3 = 3/8$.
Se i tre initiators non sono in fila, ritorniamo al caso precendete e abbiamo $q = 1/4$.

In generale quindi, se mi trovo nella griglia con le diagonali, aumentare il numero di initiators mi aiuterebbe solo nella diffusione di $A$ all'interno di un rettangolo finito. All'interno di questo rettangolo infatti avrei $q \approx 1/2$, ma per poter uscire e diffondere $A$ nella restante porzione della rete necessiterei comunque di $q = 3/8$.

Possiamo quindi concludere osservando che la capacità di cascata della griglia è $3/8 < 1/2$, e quindi in una griglia, per potersi diffondere, $A$ deve essere migliore di $B$. Nella griglia esiste anche un intervallo di valori, quando $q \in (3/8, 1/2)$, che in cui $A$ è meglio di $B$, ma comunque la cascata non parte.

2.3 Capacità di Cascata Massima

Andiamo adesso a dimostrare un risultato generale rispetto alla capacità di cascata di una rete. L'enunciato che vogliamo dimostrare è il seguente

Teorema: Per ogni grafo $G$, la capacità di cascata massima di $G$ è $q_g \leq \frac12$.

Notiamo che il teorema ci sta dicendo che, a prescindere dalla particolare topologia della rete $G$, per poter diffondersi completamente in una rete, la nuova tecnologia $A$ deve essere almeno buona quanto quella di $B$, ovvero $a \geq b$.

Dimostrazione: Consideriamo una rete con tutti i nodi inizialmente nello stato $B$ e supponiamo di regalare la nuova tecnologia $A$ ad un numero finito di nodi. Supponiamo che $q > 1/2$, ovvero che il nuovo prodotto $A$ è di qualità scadente rispetto al vecchio prodotto $B$. Per dimostrare il teorema dobibamo dimostrare che con questo $q$ non si riesce a far partire la cascata, e quindi che il prodotto $A$ non riuscirà a diffondersi nella rete.

Motivati da questo, consideriamo i seguenti insiemi di nodi

$V_0 := \text{ initiators }$

$V_t := \text{nodi che adottano } A \text{ al passo } t$

$S_t := \bigcup\limits_{i \leq t} S_i = V_0 \cup V_1 \cup V_2 \ldots \cup S_t$

Notiamo che gli insiemi $S_i$ formano una "successione decrescente di insiemi", ovvero che

\[S_0 \subseteq S_1 \subseteq S_2 \subseteq S_3\ldots \subseteq S_t \subseteq \ldots\]

Definiamo a questo punto l'interfaccia al passo $t$ come il seguente insieme

\[I_t = \{(u, v) \in E: \,\, u \in S_t \,\, \land \,\, v \in V - S_t\}\]

Detto in modo informale $I_t$ contiene tutti gli archi che collegano un nodo "contagiato", ovvero un nodo che ha adottato la nuova tecnologia $A$, ad un nodo "sano", ovvero un nodo che utilizza ancora la tecnologia $B$. Graficamente troviamo,

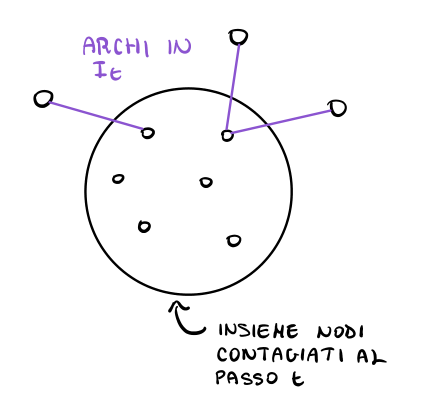
La dimostrazione del teorema si riduce quindi alla dimostrazione del seguente claim

\[q > \frac12 \implies \forall t: \,\,\,\, \Big[ |I_t| < |I_{t-1}| \;\; \lor \;\; I_t = I_{t-1} \Big]\]

In altre parole, o la dimensione dell'interfaccia diminuisce, oppure la diffusione di $A$ termina, in quanto se ad un istante di tempo $t$ vale $I_t = I_{t-1}$, allora abbiamo che $I_{t'} = I_{t'-1}$ per ogni $t' \geq t$, e quindi $A$ non si riesce più a diffondere.

Notiamo poi che se il claim è vero, il caso $|I_t| < |I_{t-1}|$ può essere al più $|I_0|$ volte, che è anche il numero di archi uscenti da $V_0$. Infatti, dato che $|I_0|$ è un numero fissato, per avere

\[|I_t| < |I_{t-1}| < \ldots < |I_0|\] devo per forza sottrarre almeno $1$ ad ogni step, e quindi il massimo numero di steps che possono ottenere sono proprio $|I_0|$ prima di arrivare ad una interfaccia con $0$ archi. Questo significa che, se $q > 1/2$, dopo un numero finito di passi il processo di diffusione termina senza generare alcuna cascata.

La dimostrazione del claim verrà divisa nei seguenti passi

Sia $(u, v) \in I_t$, con $u \in S_t$, $v \in V - S_t$, e supponiamo che $v$ venga contagiato al passo $t+1$, ovvero $v \in S_{t+1}$. Allora abbiamo che

\[\begin{split} &\;\;\;\;\;\;\;\;\; \frac{|N(v) \cap S_t|}{|N(v)|} \geq q > \frac12 \\ &\iff |N(v) \cap S_t | > \frac{|N(v)|}{2} \end{split}\]

Inoltre, dal fatto che possiamo esprimere il numero di vicini di $v$ dividendoli tra quelli infetti al tempo $t$ e quelli non infetti al tempo $t$, ovvero come $|N(v)| = |N(v) - S_t| + |N(v) \cap S_t|$, segue che

\[\begin{split} &\;\;\;\;\;\;\;\;\; |N(v) \cap S_t| > \frac{|N(v) - S_t|}{2} + \frac{|N(v) \cap S_t|}{2} \\ \\ &\iff \frac{|N(v) \cap S_t|}{2} > \frac{|N(v) - S_t|}{2} \\ \end{split}\]

Ricapitolando, abbiamo trovato che

\[v \in S_{t+1} \implies \;\;\; |N(v) - S_t| < |N(v) \cap S_t|\]

il che intuitivamente ha senso, in quanto ci dice che se il nodo $v$ viene infettato al tempo $t+1$, allora al tempo $t$ più della meta dei vicini di $v$ stavano in $S_t$.
A questo punto introduciamo un nuovo insieme. In particolare indichiamo con $I_t^0$ la porzione dell'interfaccia che non cambia tra il passo $t$ e il passo $t+1$. Formalmente quindi troviamo,

\[I_t^0 := \{(u, v): \,\, (u, v) \in I_t \cap I_{t+1}\}\]

Notiamo che possiamo scrivere l'insieme $I_t$ spezzandolo in due parti: una parte è formata dagli archi che nel prossimo step, al tempo $t+1$, non portano a nuovi contagi, e dunque che rimangono nell'interfaccia; un'altra parte invece è formata dagli archi che nello step $t+1$ portano a nuovi contagi. In formula troviamo,

\[I_t = \underbrace{I_t^0}_{\text{Archi che non} \\ \text{portano a nuovi contagi}} \bigcup \;\;\;\;\; \bigg[ \;\; \underbrace{\bigcup\limits_{v \in S_{t+1} - S_t} \{ (u, v): \,\, u \in S_t\}}_{\text{archi che portano} \\ \text{a nuovi contagi}} \;\;\; \bigg]\]

Siamo adesso in grado di calcolare la cardinalità di $I_t$. Infatti vale la seguente cosa

\[\begin{split} \phantom{} |I_t| &= |I_t^0| + |\bigcup\limits_{v \in S_{t+1} - S_t} \{ (u, v): \,\, u \in S_t\}| \\ &= |I_t^0| + \sum\limits_{v \in S_{t+1} - S_t} |\{ (u, v): \,\, u \in S_t\}| \\ &= |I_t^0| + \sum\limits_{v \in S_{t+1} - S_t} |N(v) \cap S_t| \\ \end{split}\]

Infatti abbiamo che la cardinalità dell'unione è uguale alla somma delle cardinalità, in quanto gli insiemi della forma $\{(u, v): \,\, u \in S_t\}$ al variare di $u$ sono insiemi distinti. Inoltre è possibile notare come gli insiemi $\{(u, v): \,\, u \in S_t\}$ e $\{N(v) \cap S_t\}$ hanno lo stesso numero di elementi.

Così facendo abbiamo espresso la cardinalità di $I_t$ come somma tra una parte invariante, $I_t^0$, e una parte che varia, $N(v) \cap S_t$, con $v \in S_{t+1}$.
Facciamo adesso la stessa cosa con $I_{t+1}$, ovvero con l'interfaccia al tempo $t+1$. A tale fine notiamo che

\[I_{t+1} = I_t^0 \bigcup \,\, \bigg[ \bigcup\limits_{v \in S_{t+1} - S_t} \{(u, v): \,\, u \in V - S_{t+1}\}\bigg]\]

Nuovamente, possiamo calcolare la cardinalità di $I_{t+1}$ nel seguente modo

\[\begin{split} \phantom{} |I_{t+1}| &= |I_t^0| + \bigg|\bigcup\limits_{v \in S_{t+1} - S_t} \{(u, v): \,\, u \in V - S_{t+1}\}\bigg| \\ &= |I_t^0| + \sum\limits_{v \in S_{t+1} - S_t} |\{(u, v): \,\, u \in V - S_{t+1}\}|\\ &= |I_t^0| + \sum\limits_{v \in S_{t+1} - S_t} | N(v) - S_{t+1} | \end{split}\]

Infatti nuovamente possiamo esprimere la cardinalità dell'unione come somma di cardinalità, in quanto gli insiemi sono disgiunti, e nuovamente il numero di elementi dell'insieme $\{(u, v): \,\, u \in V - S_{t+1}\}$ è uguale al numero di elementi dell'insieme $N(v) - S_{t+1}$.
Utilizzando il fatto che $S_t \subseteq S_{t+1}$ troviamo la seguente disuguaglianza

\[|N(v) - S_{t+1}| \leq |N(v) - S_t|\]

Infine, utilizzando la relazione ottenuta al passo $(1)$, troviamo

\[\begin{split} \phantom{} |I_{t+1}| &= |I_t^0| + \sum\limits_{v \in S_{t+1} - S_t} | N(v) - S_{t+1} | \\ &\leq |I_t^0| + \sum\limits_{v \in S_{t+1} - S_t} | N(v) - S_{t} | \\ &< |I_t^0| + \sum\limits_{v \in S_{t+1} - S_t} | N(v) \cap S_{t} | \\ &= |I_t| \end{split}\]

Concludendo, abbiamo dimostrato che se c'è un nodo contagiato al passo $t+1$, allora la dimensione dell'interfaccia diminuisce, e quindi il claim è verificato.

\[\tag*{$\blacksquare$}\]