AR - 15 - Ricerca Decentralizzata I
Lecture Info
Data:
Capitolo Libro: Chapter 20 - The Small-World Phenomenon
Introduzione: In questa lezione abbiamo iniziato a studiare il fenomeno dello "small world", noto anche con il nome "6 gradi di seperazione", concetti che derivano da un esperimento effettuato e successivamente descritto da Milgram negli anni '60. In particolare sono stati definiti vari modelli matematici, al fine di capire quali sono le caratteristiche che una rete sociale deve avere per ottenere risultati simili a quelli ottenuti da Milgram.
1 Teoria del Mondo Piccolo
Consideriamo il modello generativo di Erdős-Rényi. È possibile dimostrare che il diametro di un grafo generato da tale modello è piuttosto alto, essendo dell'ordine di \(O(\sqrt{n})\).
Questo tendenzialmente non è vero per le reti sociali reali. Empiricamente infatti, a partire dall'esperimento effettuato da Milgram, che ha poi introdotto il concetto dei "6 gradi di separazione" e più in generale il fenomeno dello small world, sono stati effettuati vari studi che fanno vedere come le reti sociali reali tendono ad avere un diametro molto piccolo rispetto al numero di nodi.
Nel suo esperimento, descritto nel seguente articolo, Milgram chiese a degli individui "starters" scelti in modo randomico di provare a consegnare una lettera ad un determinato individuo "target". Le uniche informazioni che Milgram diede agli "starters" erano il nome, l'indirizzo, l'occupazione, e qualche informazione personale del "target". Il vincolo imposto era il seguente: i partecipanti non potevano spedire in modo diretto la lettera al "target", ma dovevano inviare la lettera ad una persona di cui conoscevano almeno il nome, cercando così facendo far avvicinare il più possibile la lettera al "target". I risultati ottenuti dall'esperimento sono stati alquanto sorprendenti: approssimatamente \(1/3\) delle lettere era riuscito ad arrivare al target, con una media di \(6\) passi per lettera.
L'esperimento di Milgram mette in risalto i seguenti aspetti delle reti sociali di dimensione significativa:
Esistono tante shortes paths nelle reti sociali.
Le persone, effettuando delle scelte locali senza nessun tipo di organizzazione centralizzata, sono in grado di percorrere in modo efficiente queste shortest paths.
1.1 Numero di Shortest Paths
Nasce dunque il problema di rispondere alla seguente domanda: perché ci sono tante shortest paths nelle reti sociali?
Una prima risposta potrebbe considerare il fatto che l'elevato numero di relazioni di amicizia, o anche solo di conoscenza, che ciascun individuo ha porta a diminuire il diametro della rete, in quanto è possibile raggiungere tantissimi nodi passando da una amicizia ad un'altra. Ad esempio se supponiamo che ciascuna persona conosce altre \(100\) persone, si potrebbe supporre di avere una crescita esponenziale nel numero di persone raggiungibili come descritta dalla seguente figura
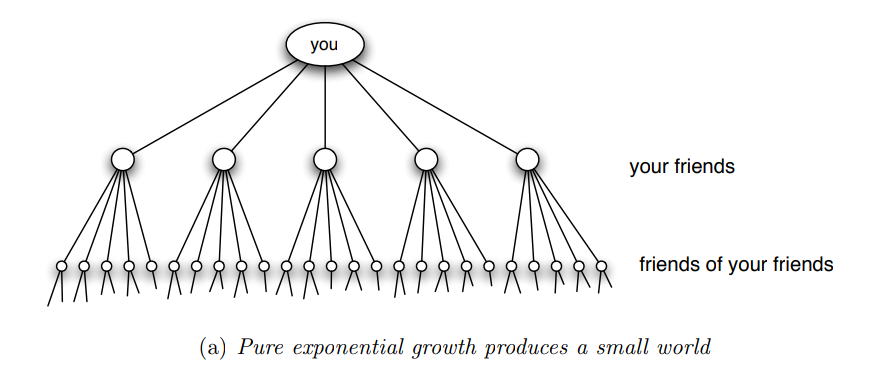
Notiamo però che la crescita esponenziale appena descritta non tiene in considerazione che nelle reti sociali l'omofilia e la chiusura triadica giocano un ruolo fondamentale nella creazione delle relazioni. In altre parole, molti dei nostri amici e conoscenti si potrebbero conoscere tra loro, andando così a diminuire il numero diverso di amici e conoscenti che possiamo raggiungere. Una figura più realistica è quindi la seguente
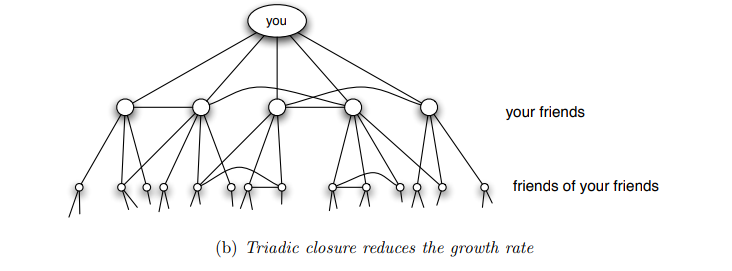
Questo significa che nelle reti sociali la chiusura triadica, discussa in una precedente lezione, tende a limitare il numero di persone che possono essere raggiunte seguendo i cammini brevi della rete.
1.2 Ricerca Decentralizzata
Un altro aspetto fondamentale emerso dai risultati ottenuti da Milgram è stato il fatto che gli individui sono stati collettivamente in grado di trovare dei cammini brevi per arrivare al target.
Notiamo che la ricerca effettuata dai partecipanti dell'esperimento non può essere considerata né una ricerca centralizzata e né una ricerca distribuita. Ogni individuo infatti effettuava le proprie scelte personali, senza coordinarsi in modo consapevole con gli altri individui. Questo tipo di ricerca prende il nome di ricerca decentralizzata.
Nasce quindi il seguente quesito: perché le reti sociali sono strutturate in modo da rendere questo tipo di ricerca decentralizzata così efficiente?
2 Modelli Mondo Piccolo
Cerchiamo adesso di definire dei modelli matematici che catturano le caratteristiche appena discusse.
2.1 Modello di Watts-Strogatz
Il primo modello che analizziamo è il modello di Watts-Strogatz. L'idea alla base di questo modello è semplice: si parte da un grafo a griglia con le diagonali (unit-disk graph), e lo si modifica andando ad aggiungere degli archi random scelti in modo uniforme.
Notiamo come la struttura base del grafo a griglia con l'aggiunta delle diagonali permette di catturare la parte omofila di una rete sociale
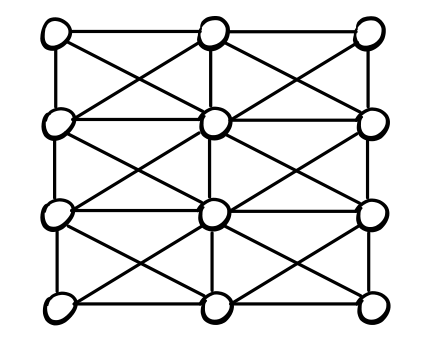
La griglia di base però non ci permette di avere tante shortest paths. Per aumentare il numero di shortest paths quindi si aggiungono degli archi random nel seguente modo: Si fissa un valore del parametro \(k \in \mathbb{N}\) e si collega ogni nodo della griglia con altri \(k\) nodi scelti in modo uniforme. Notiamo che questi archi random aggiunti hanno la funzione di weak-ties, ovvero il loro obiettivo è quello di portare nuova informazioni nella rete, andando così ad aumentare il numero di shortest paths. Troviamo quindi la seguente figura
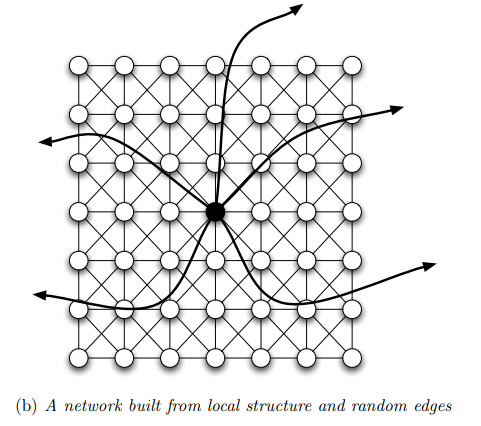
È possibile dimostrare che il grafo random costruito in questo modo contiene tante shortest paths. Intuitivamente questo segue dal fatto che, se abbiamo costruito la rete come descritto, e se abbiamo tanti nodi, allora è molto improbabile che gli archi aggiunti come weak ties collegano nodi tra loro vicini. Dunque gli archi aggiunti permettono di ricoprire l'intera rete.
Osservazione: In realtà è possibile dimostrare un risultato più forte: il numero di shortest paths è alto anche se facciamo partire un solo arco in modo uniforme da ogni cluster di \(k\) nodi. Dunque ci basta una quantità di randomness molto limitata per ottenere gli stessi risultati.
Anche se il modello di Watts-Strogatz appena descritto è in grado di catturare bene il fatto che nelle reti sociali ci sono tanti shortest paths, gli archi aggiunti risultano essere troppo random, in quanto i nodi vengono collegati senza far riferimento a nessun concetto di "distanza" o gradiente. Come conseguenza di ciò, nel modello di Watts-Strogatz non è possibile risolvere in modo efficiente il problema della ricerca decentralizzata discusso in precedenza.
2.2 Modello per Ricerca Decentralizzata
Andiamo adesso a descrivere un modello che contiene tante shortest paths e che ci permette di risolvere in modo efficiente il problema della ricerca decentralizzata.
Seguendo l'idea di Watts-Strogtaz, iniziamo con una griglia in grado di catturare l'omofilia delle reti sociali. Supponiamo inoltre che la griglia sia poggiata su una sfera, per ottenere la massima simmetria. Seguendo sempre il modello Watts-Strogtaz, introduciamo alcuni archi random che serviranno da weak ties. Questa volta però gli archi vengono introdotti utilizzando una nozione di distanza. In particolare, ogni nodo ha un solo weak tie descritto dalla seguente distribuzione di probabilità
\[P[(u, v) \in E] = \frac{1}{z_u} \cdot \frac{1}{d(u, v)^q}\]
dove,
\(z_u\) è una costante di normalizzazione.
\(d(u, v)\) è la distanza tra \(u\) e \(v\) nella griglia iniziale.
\(q\) è un parametro del modello chiamato esponente di clustering.
Notiamo che la costante \(z_u\) è necessaria al fine di avere una distribuzione di probabilità. Per trovare il valore di \(z_u\) imponiamo quindi la seguente equivalenza
\[\begin{split} &\;\;\;\;\;\;\;\;\;\;\; \sum\limits_{v \in V - \{u\}} P[(u, v) \in E] = 1 \\ &\iff \frac{1}{z_u} \cdot \sum\limits_{v \in V - \{u\}} \frac{1}{d(u, v)^q} = 1 \\ &\iff z_u = \sum\limits_{v \in V - \{u\}} \frac{1}{d(u, v)^q} \end{split}\]
Notiamo che anche se tecnicamente la costante di normalizzazione \(z_u\) è specifica per il singolo nodo \(u\), data la simmetria del grafo con cui stiamo lavorando abbiamo che per ogni coppia di nodi \(u, v\) vale \(z_u = z_v\), e dunque la possiamo considerare la costante di normalizzazione come un singolo valore \(z\) uguale per tutti i nodi.
Il parametro \(q\) invece viene utilizzato per controllare il processo di creazione degli weak-ties. A tale fine notiamo che
Se \(q = 0\), allora \(z = n - 1\) e quindi
\[P[(u, v) \in E] = \frac{1}{n-1}\]
ovvero la creazione dei weak ties si riduce ad una scelta uniforme, riducendo così il modello al modello di Watts-Strogtaz visto prima.
In generale all'aumentare di \(q\) diminuisce la probabilità di trovare weak-ties tra nodi lontani, come mostra la seguente figura
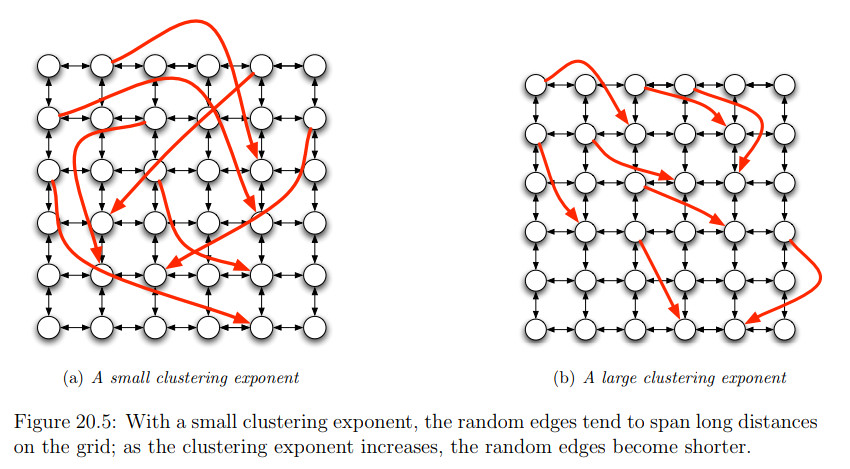
Al fine di trovare un modello che ci aiuti nella ricerca decentralizzata siamo quindi interessati a trovare valori di \(q\) tali che
Sia possibile raggiungere nodi "abbastanza" lontani utilizzando i weak ties;
I nodi collegati dai weak ties non devono però essere "troppo" lontani tra loro.
Sperimentalmente è stato dimostrato che un valore ideale per \(q\) è dato dalla dimensione dello spazio in cui ci troviamo. Dunque, se stiamo in uno spazio a tre dimensioni, allora \(q = 3\); se invece stiamo in un piano a due dimensioni, come la griglia appena descritta, allora \(q = 2\). Infine, se ci troviamo in un anello ad una dimensione, abbiamo che \(q = 1\).
2.2.1 Perché \(q=2\) è ottimo nel piano?
Per terminare la lezione, cerchiamo di capire intuitivamente il perché nel piano il parametro \(q=2\) è ottimo. Nella prossima lezione dimostreremo formalmente il risultato quando ci troviamo nell'anello.
L'idea alla base è che, nel mondo reale, organizziamo mentalmente le distanze rispetto a varie scale di risoluzione. In particolare quindi possiamo pensare a qualcosa che si trova nello stesso nostro quartiere, oppure nella stessa nostra città, oppure nella stessa nostra regione, e via dicendo. Per poter essere efficiente, una ricerca decentralizzata deve necessariamente muoversi in varie scale di risoluzione, in modo da arrivare il prima possibile al destinatario. In particolare nelle prime fasi della ricerca si tende ad aumentare la scala di risoluzione, e poi ad un certo punto si comincia a diminuire, fino a raggiungere l'obiettivo. Graficamente troviamo il seguente schema
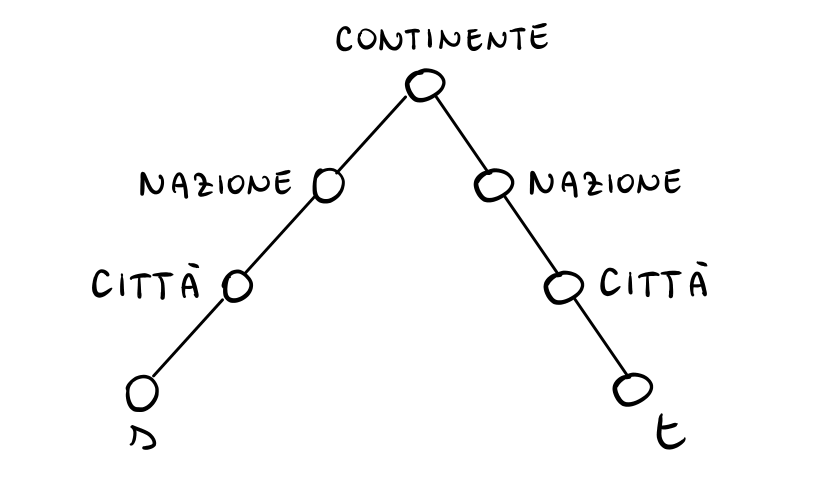
Possiamo formalizzare questo concetto di "scale di risoluzione" come segue: consideriamo la visione di un nodo \(u \in V\) rispetto agli altri nodi dividendola rispetto a intervalli di distanza crescente. In particolare consideriamo prima tutti i nodi che si trovano ad una distanza tra \(2\) e \(4\), poi tutti i nodi che si trovano ad una distanza tra \(4\) e \(8\), e via dicendo.
Supponiamo che \(q = 2\), fissiamo un parametro \(d \in \mathbb{N}\), e consideriamo tutti i nodi compresi tra una distanza \(d\) e \(2 \cdot d\) dal nodo \(v\).
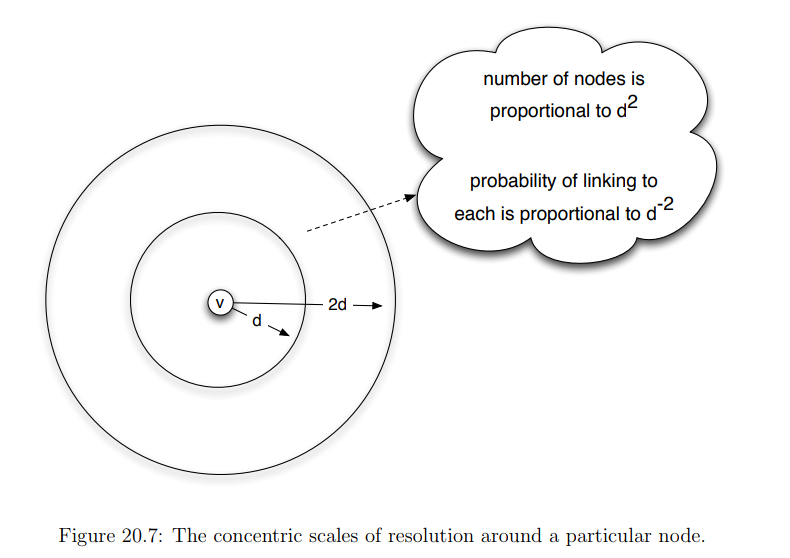
Osserviamo a questo punto che,
Dato che l'area nel piano cresce come il quadrato del raggio, abbiamo che il numero totale di nodi dentro questo gruppo è proporzionale a \(d^2\).
Dato che abbiamo \(q=2\), la probabilità che \(v\) sia collegato ad un nodo dentro questo gruppo è proporzionale a \(d^{-2}\).
Questi due termini si semplificano, e quindi la probabilità che l'arco random che parte da \(v\) colleghi \(v\) ad un qualche nodo dentro questo anello è approssimatamente indipendente dal valore di \(d\). Detto altrimenti, se ci troviamo nel piano, il valore di \(q = 2\) ci permette di distribuire i weak ties in modo approssimatamente uniforme in tutte le scale di risoluzione, e questo rende possibile una ricerca decentralizzata efficiente.