CNS - 34 - Secret Sharing I
Lecture Info
Date:
Lecturer: Giuseppe Bianchi
Slides: (40-ss.pdf)
Introduction: This lecture starts the final third module of the course, in which we will explore more advanced topics in applied cryptography. In this lecture in particular we will see techniques for secret sharing.
1 Trivial Secret Sharing
Secret sharing is a technique that lets me share a secret among different people such that only when all the people are reuineted the secret is reconstructed.
Consider in the following discussion that we want to share the secret \(\text{0010.1101}\). One of the first (very bad) idea is to simply split the secret into two parts.
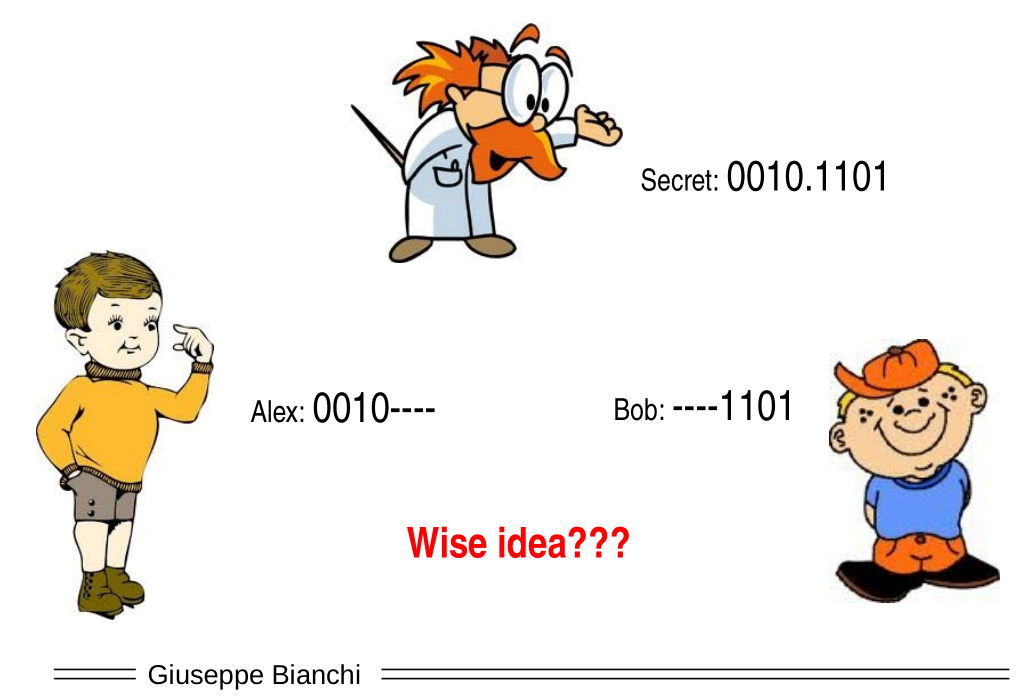
Notice that this idea is really, really bad, because now for an attacker its much, much easier to guess one of the halves of the password: if initially the probability to guess randomly was \(1/256\), after splitting it it becomes \(1/16\), which is much better.
1.1 With XOR
A better solution, called trivial secret sharing, consists in generating a random sequence like \(\text{1011.0100}\) and then computing the XOR between the secret and the random quantity
\[\text{Secret} \mathbin{\oplus} \text{Random} = \text{0010.1101} \mathbin{\oplus} \text{1011.0100} = \text{1001.1001}\]
You then give to Alex the random sequence, and to bob you give the XORed value. With this approach when the two people meet they can just XOR their value to obtain the original secret.
Now, notice that Alex is given a random sequence, and therefore he has no information about the secret. Does the string that Bob receives contain any information about the secret? No, because we can consider the string given to Bob as the result of the Vernman cipher, obtained by xoring the secret (plain text) with a random sequence, and, as we proved in the 2nd lecture the following holds
\[\text{Information bit} \mathbin{\oplus} \text{random bit} = \text{random bit}\]
1.2 With modular sums
To implement the previous schema another solution can be used. This time, instead of the XOR operation, one can make use of modular sums. In particular, our message as a number, we can generate a random number between 0 and 256, and we can consider original number minus the generated one. In particular we have the following associations
\[\begin{split} \text{Secret } = &\text{ 0010.1101}& &\longrightarrow 45 \\ &\text{RAND} &\mod 256 &\longrightarrow 180 \\ &S - \text{RAND} &\mod 256 &\longrightarrow 121 \\ \end{split}\]
We can then give the value \(180\) to a person, and the value \(121\) to another person. Notice that if the random value is uniformly distributed, also the \(S - \text{RAND}\) value will be uniformly distributed, and thus the attacker cannot gain additional information on the secret starting from one of the values.
Observation 1: Notice that the modulus operator is not necessary, meaning that the result also works without it. However, it is very pratical to use it, since modular arithmetic makes everything much simpler to use and implement.
Observation 2: The modulus is not required to be a prime number.
1.3 Extension to \(n\) parties
The owner of the secret is typically called the dealer. Consider now the situation where the dealer wants to share a secret with \(4\) people, such that only when the four people are together the secret is revelead.
The idea is a natural extension of the previous one: generate \(3\) quantities, \(R_1, R_2, R_3\), and compute the fourth one by subtracting them from \(S\). Then assign to each person one of the computed values.
\[\begin{split} S &\longrightarrow 45 \\ R_1 &\longrightarrow 135 \\ R_2 &\longrightarrow 6 \\ R_3 &\longrightarrow 67 \\ S - R_1 - R_2 - R_3 &\longrightarrow 93 \\ \end{split}\]
Perfect secrecy in this context means that the probability of guessing the secret after \(n-1\) shares are revelead is still the same as the probability of guessing the secret before seeing any shares.
2 Shamir Secret Sharing
We will now see a more complex secret sharing technique, the shamir secret sharing. It is important however to keep in mind that, as long as you just need to simply share a secret with \(n\) people, it is better to use the trivial secret sharing technique.
Consider the following two sharing schemes:
(n, n) secret sharing scheme: In this scheme the secret is revealed only if all \(n\) parties provide a share. This scheme is solved by the trivial secret sharing technique seen previously.
(t, n) secret sharing scheme: In this scheme the secret is revealed only when any \(t\) (threshold value) out of \(n\) parties provide a share, with \(1 \leq t \leq n\). If \(t = 1\), then every partner has a secret and we reduce to the trivial case.
In 1979 Shamir wrote a revolutionary 2 pages paper which introduced the concept of (t, n) schemes. In his words,
Eleven scientists are working on a secret project. They wish to lock up the documents in a cabinet so that the cabinet can be opened if and only if six or more of the scientists are present. What is the smallest number of locks needed? 462 What is the smallest number of keys to the locks each scientist must carry? 252
There is evidence (President, Defense Minister, and Defense Ministry (Beimel, 2010)) that a two-out-of-three nuclear weapon control was used in Russia in the early 1990s. In general (t, n) schemes have become basic building block in several cryptographic constructions, such as group cryptography.
This problem was solved by two different people in the same year (1979):
Shamir
Blakley
Everyone now remembers more Shamir solution but his solution was the optimal one, while Blakley solved the same problem but his solution was not as optimal.
2.1 \((2, n)\) scheme
Consider a (2, n) scheme, that is a scheme in which something is revealed only if \(2\) people provide some information.
Remember that two points uniquely define a single line. Indeed, given only a single point there are infinite lines that pass through it
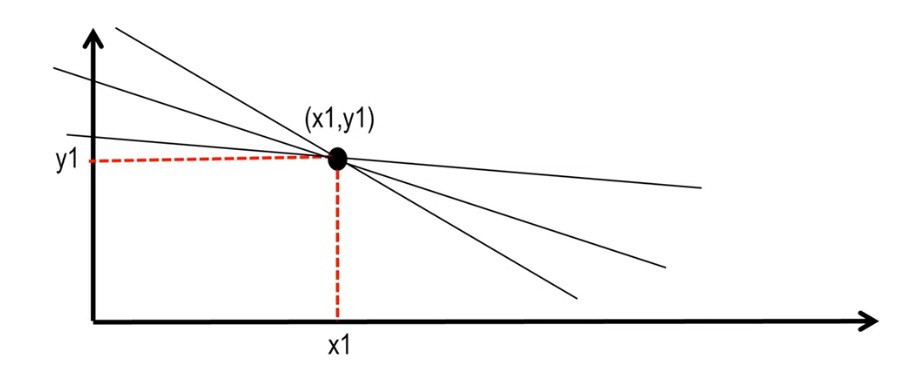
Then, if I give you a single point more, then only a single line emerges.
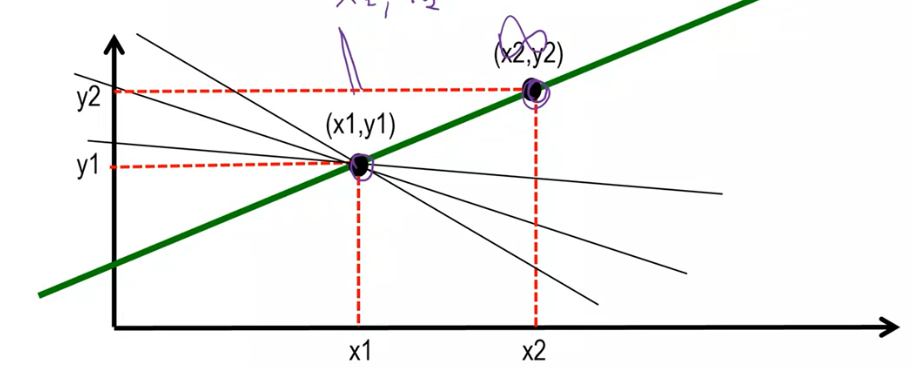
The idea then is to have the secret being the y-intercept of the line. I can then have as many points on my line as I want, and only when two or more people more they are able to compute the equation for the line and thus to find the secret.
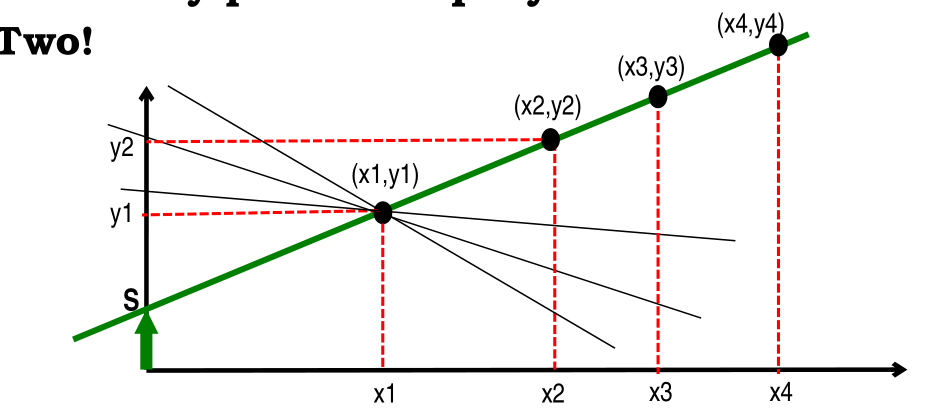
More formally thus we have
The secret S is the y-value at \(x = 0\)
The share for user \(i\) is the point \((x_i, y_i)\)
Let us now see the mathematical details of such construction
2.1.1 Dealing
The line that is constructed by the dealer is given by the following equation
\[y = S + a \cdot x\]
where \(a\) is a randomly choosen coefficient and \(S\) is the secret we want to protect. Once we have constructed the equation we distribute one share to each of the \(n\) participants:
\(\text{share}_1 = (x_1, \,\, S + a \cdot x_1)\)
\(\text{share}_2 = (x_2, \,\, S + a \cdot x_2)\)
\(\text{share}_3 = (x_3, \,\, S + a \cdot x_3)\)
Notice that in the construction the \(x_i\) values can be public. Only the particular height of of the point (the y value) has to be private.
Example: If \(a = 15\) and \(S = 39\) we get the line \(y = 39 + 15x\) and we give the following shares
\(\text{share}_1 = (1, \,\, 39 + 15 \cdot 1) = (1, 54)\)
\(\text{share}_2 = (x_2, \,\, 39 + 15 \cdot 2) = (2, 69)\)
\(\text{share}_3 = (x_3, \,\, 39 + 15 \cdot 3) = (3, 84)\)
2.1.2 Reconstructing
Let us now see how we would go on for reconstructing the secret. Since this is a (2, n) scheme, to reconstruct the secret we need two shares. Suppose then we receive the following shares
\[P_i = (x_i, y_i) \,\,\,\, P_j = (x_j, y_j)\]
the idea is to interpolate the points of the line to get the following
\[\frac{y - y_j}{y_i - y_j} = \frac{x - x_j}{x_i - x_j} \implies y = y_j + \frac{y_i - y_j}{x_i - x_j} \cdot (x - x_j)\]
Then, to derive the secret \(S\), we just need to set \(x = 0\) to get
\[S = y_j + \frac{y_i - y_j}{x_i - x_j} \cdot (0 - x_j) = y_j \frac{-x_i}{x_j - x_i} + y_i \frac{-x_j}{x_i - x_j}\]
Example: If \(P_i = (3, 84)\), \(P_j = (1, 54)\) we get
\[y = 54 + 15(x - 1)\]
and thus if we set \(x=0\) we obtain
\[S = 54 + 15(0-1) = 54 - 15 = 39\]
2.2 \((t, n)\) scheme
The previous idea can then be generalized to \(n\) points. Consider for example a parabola, which is defined by three points. Or a cubic, which is defined by four points. In general the following scheme holds
\[\begin{split} (2, n) &\leftrightarrow \text{first order polynomial (line)} \\ (3, n) &\leftrightarrow \text{second order polynomial (parabola)} \\ (4, n) &\leftrightarrow \text{third order polynomial (cubic)} \\ &\,\,\,\,\vdots \\ (t, n) &\leftrightarrow t-1 \text{ order polynomial} \\ \end{split}\]
Even though the math required to find a valid interpolation may be harded to express, the conceptual idea behind is the same as the one used for the (2, n) scheme.
2.2.1 Lagrange Interpolation
There are various formulas that can be used to interpolate \(t\) different points. The most convenient of them all is Lagrange interpolation, which allows you to reconstruct the equation of a polynomial of an arbitrary order (say order \(t\)), as long as you have \(t+1\) points. This method is based on the following result:
Lagrange Theorem: Any polnoymial of degree \(t-1\) with \(t\) known points \((x_1, y_1\), ..., \((x_t, y_t)\) can be decomposed as follows
\[y = \sum\limits_{i = 1}^t y_i \Lambda_i(x)\]
Where \(\Lambda_i(x)\) is the basis polynomial defined as
\[\Lambda_i(x) = \prod\limits_{m = 1, m \neq i}^t \frac{x - x_m}{x_i - x_m} = \frac{(x - x_1)}{(x_i - x_1)} \cdot \ldots \cdot \frac{(x - x_{i-1})}{(x_i - x_{i-1})} \cdot \frac{(x - x_{i+1})}{(x_i - x_{i+1})} \cdot \ldots \cdot \frac{(x - x_t)}{(x_i - x_t)}\]
To construct such polynomial you can use the following recipe: Consider all the points of the other guys. For each such point you construct a nominator by subtracting the point from \(x\), and a denominator by subtracting the point from your own point. Then you multiply all nominators together and then divide by all the denominators.
It comes out that all these polynomials \(\Lambda_i(x)\) form an ortonormal basis basis for a vector space
\[\Lambda_i(x_i) = 1 \,\,\,, \,\,\, \Lambda_i(x_m) = 0 \,\, m \neq i\]
The geometrial interpretation is showed in the following image
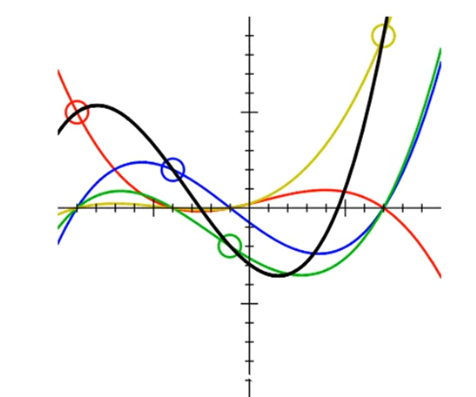
In particular notice that at the point \(x = 0\) we get the following value
\[\Lambda_i(0) = \prod\limits_{m = 1, m \neq i}^t \frac{- x_m}{x_i - x_m}\]
2.2.2 Dealing
Since I want a (t, n) scheme, the idea is to generate a polynomial \(p(x)\) with degree \(t-1\) and set the secret \(S\) as the known term in the polynomial
\[p(x) = S + a_1 x + a_2 x^2 + \ldots + a_{t-2} x^{t-2} + a_{t-1} x^{t-1}\]
You then distribute one share to each of the \(n\) parties.
\[(x_i, y_i) = y_i = p(x_i) \,\,\, i = 1, \ldots, n\]
Notice that we are assuming that \(n > t\), for otherwise there are much simpler approaches to the problem.
2.2.3 Reconstructing
To reconstruct the idea is to collect the \(t\) shares out of the \(n\) available and compute the secret using the lagrange interpolation at \(x = 0\).
\[S = \sum\limits_{\text{shares } x_i}y_i \Lambda_{x_i}\]
where for every share \(x_i\) we have that
\[\Lambda_{x_i} = \Lambda_{x_i}(0) = \prod\limits_{\text{shares } x_k \neq x_i} \frac{-x_k}{x_i - x_k}\]
2.3 \((3, 4)\) scheme
Let us now see a real application of the scheme described below to construct a (3, 4) scheme. We start by generating the following polynomial
\[p(x) = 32 + 52x + 3x^2\]
and we give out the following shares to each participant:
\(\text{share}_1 = (1, p(1)) = (1, 87)\)
\(\text{share}_2 = (2, p(2)) = (2, 87)\)
\(\text{share}_3 = (3, p(3)) = (3, 215)\)
\(\text{share}_4 = (4, p(4)) = (4, 288)\)
Each participant can then compute his/her own particular lambda polynomial
\[\begin{split} \Lambda_1(x) &= \frac{(x - x_2)}{(x_1 - x_2)} \cdot \frac{(x - x_3)}{(x_1 - x_3} = \frac12 (-3 +x)(-2 + x)\\ \\ \Lambda_2(x) &= \frac{(x - x_1)}{(x_2 - x_1)} \cdot \frac{(x - x_3)}{(x_2 - x_3} = (3-x)(-1+x)\\ \\ \Lambda_3(x) &= \frac{(x - x_1)}{(x_3 - x_1)} \cdot \frac{(x - x_2)}{(x_3 - x_2} = \frac12 (-2 + x) (-1 + x)\\ \end{split}\]
Notice that each polynomial obtained has degree two. This makes sense, since we have to reconstruct a parabola. Indeed, if we actually compute the Lagrange interpolation we get
\[\begin{split} y_1 \Lambda_1(x) + y_2 \Lambda_2(x) + y_3 \Lambda_3(x) &= \frac{87}{2}(-3 +x) (-2 + x) \,\, + \\ &\;\;\;\;\;\; 148(3-x) (-1+x) \,\, + \\ &\;\;\;\;\;\; \frac{215}{2}(-2 + x)(-1+x) \\ \end{split}\]
which, when simplified, gives us exactly the original polynomial
\[y_1 \Lambda_1(x) + y_2 \Lambda_2(x) + y_3 \Lambda_3(x) = 3x^2 + 52x + 32\]
For actually reconstructing the secret we don't care about using the entire polynomial. Rather, we are more interesting in computing the polynomials computed for the point \(x = 0\).
\[\begin{split} \Lambda_1(0) &= \frac12 (-3 + 0)(-2 + 0) = 3\\ \\ \Lambda_2(0) &= (3 - 0)(-1 + 0) = -3\\ \\ \Lambda_3(0) &= \frac12 (-2 + 0) (-1 + 0) = 1\\ \end{split}\]
The secret is then reconstructed as follows
\[\begin{split} S &= \sum\limits_{\text{shares } x_i}y_i \Lambda_{x_i} \\ &= y_1 \cdot \Lambda_1(0) + y_2 \cdot \Lambda_2(0) + y_3 \cdot \Lambda_3(0) \\ &= 261 + -444 + 215 \\ &= 32 \\ \end{split}\]
2.4 Is it secure?
What we would like to have is an uncoditionally secure scheme, meaning that the knowledge of any \(t-1\) or fewer shares leave the secret \(S\) undetermined.
Notice that the scheme we have discussed so far its not an uncoditionally secure scheme. Consider for example the previous example, and suppose that we have found out share \(y_1\) and share \(y_3\). Then we can replace \(y_2\) with a variable \(d\) to find the following
\[\begin{split} S &= y_1 \cdot \Lambda_1(0) + d \cdot \Lambda_2(0) + y_3 \cdot \Lambda_3(0) \\ &= 476 - 3d \\ \end{split}\]
since \(d\) is an integer we know that \(2/3\) of the values are excluded.