ML - 08 - Linear Regression
Date:
Lecturer: Giorgio Gambosi
Slides: (ml_04_linregr-slides.pdf)
In questa lezione abbiamo dato una struttura più formale rispetto a quanto visto precedentemente sulla regressione lineare.
La regressione lineare è un particolare modo per calcolare un modello lineare, ovvero un modello in cui la predizione avviene calcolanndo una combinazione lineare dei valori delle input features.
\[y(\mathbf{x}, \mathbf{w}) = w_0 + w_1x_1 + w_2x_2 + \ldots + w_Dx_D\]
dove per linare si intende che \(y(\mathbf{x}, \mathbf{w})\) è una funzione lineare rispetto ai coefficienti in \(\mathbf{w}\).
Molto spesso rappresenteremo l'espressione \(y(\mathbf{x}, \mathbf{w})\) in forma matriciale nel seguente moodo
\[(\mathbf{x}, \mathbf{w}) = \mathbf{w}^T \overline{\mathbf{x}}\]
dove \(\overline{\mathbf{x}} = (1, x_1, \ldots, x_D)\).
Tipicamente la combinazione lineare non viene fatta utilizzando direttamente i valori delle features \(x_i\), ma si utilizzando piuttosto delle funzioni, dette funzioni base, che vengono applicate rispetto ai valori delle features per ottenere nuovi valori.
In particolare si hanno \(M\) funzioni base predefinite \(\phi_1, \phi_2, \ldots, \phi_M\), ciascuna delle quali mappa il vettore delle features \(\mathbf{x} \in \mathbb{R}^D\) ad un singolo numero reale \(\phi_i(\mathbf{x})\). La combinazione lineare si trasforma quindi nel seguente modo
\[y(\mathbf{x}, \mathbf{w}) = \sum\limits_{j = 1}^M w_j \phi_j(\mathbf{x}) = w_1 \phi_1(\mathbf{x}) + w_2 \phi_2(\mathbf{x}) + \ldots + w_M \phi_M(\mathbf{x})\]
L'idea quindi è che ogni vettore \(\mathbf{x} \in \mathbb{R}^D\) viene mappato in un nuovo vettore
\[\mathbf{x} \longrightarrow \mathbf{\phi}(\mathbf{x}) = (\phi_1(\mathbf{x}), \ldots, \phi_M(\mathbf{x}))\]
Così facendo al posto di lavorare con uno spazio di \(D\) dimensioni, che sono il numero di features del problema, possiamo lavorare con uno spazio di \(M\) dimensioni. Tipicamente \(M > D\).
Observation: Trovare queste \(M\) funzioni fa parte di un'attività che prende il nome di feature engineering, e che consiste nel trasformare i valori delle features iniziali in modo tale da risolvere il problema che si vuole affrontare. Questo tipo di attività viene effettuata prima ancora di elaborare i dati, analizzando in modo generale il problema che si vuole affrontare.
Ci sono tante tipologie di funzioni base. Tra queste troviamo:
Polynomial (global functions):
\[\phi_j(x) = x^j\]
Gaussian (local):
\[\phi_j(x) = \text{exp}\Big( - \frac{(x - \mu_j)^2}{2s^2}\Big)\]
Sigmoid (local):
\[\phi_j(x) = \sigma\Big(\frac{x - \mu_j}{s}\Big) = \frac{1}{1 + e^{- \frac{x - \mu_j}{s}}}\]
Hyperbolic tangent (local):
\[\phi_j(x) = \tanh{(x)} = 2\sigma(x) - 1 = \frac{1 - e^{-\frac{x - \mu_j}{s}}}{1 + e^{-\frac{x - \mu_j}{s}}}\]
L'idea dietro alle funzioni base di tipo locale è quella di concentrare i valori diversi da \(0\) in una zona specifica.
Utilizzando delle base functions il training set su cui si lavora può essere rappresentato tramite la seguente matrice
\[\mathbf{\Phi} = \begin{pmatrix} \phi_1(\mathbf{x}_1) & \phi_2(\mathbf{x}_1) & \ldots & \phi_M(\mathbf{x}_1) \\ \phi_1(\mathbf{x}_2) & \phi_2(\mathbf{x}_2) & \ldots & \phi_M(\mathbf{x}_2) \\ \vdots & \vdots & \ddots & \vdots \\ \phi_1(\mathbf{x}_N) & \phi_2(\mathbf{x}_N) & \ldots & \phi_M(\mathbf{x}_N) \\ \end{pmatrix}\]
Come abbiamo visto nella precedente lezione, è possibile definire un modello probabilistico alla base della regressione lineare.
In particolare assumiamo la presenza di un rumore di tipo gaussiano che discosta il valore del target \(t\) dal valore predetto \(y(\mathbf{x}, \mathbf{w})\) rispetto ad un rumore \(\epsilon\)
\[t = y(\mathbf{x}, \mathbf{w}) + \epsilon\]
dove \(\epsilon \sim \mathcal{N}(0, \sigma^2)\).
Così facendo abbiamo che la probabilità di inferire il valore corretto del target \(t\) rispetto all'elemento \(\mathbf{x}\) utilizzando un modello con parametri \(\mathbf{w}\) è data da
\[P(t | \mathbf{x}, \mathbf{w}, \beta) = \mathcal{N}(t|y(\mathbf{x}, \mathbf{w}), \sigma^2)\]
dove \(\beta := 1/\sigma^2\) è detta precisione. Più alta è \(\beta\) e più i valori della gaussiana sono concentrati intorno al valor medio, e viceversa più bassa è \(\beta\) e più i valori della gaussiana sono sparsi rispetto al valor medio.
Con questo modello abbiamo che il valore atteso di \(t\) dato \(\mathbf{x}\) è dato da
\[\mathbb{E}[t|\mathbf{x}] = \int t P(t|\mathbf{x}) \,\, dt = y(\mathbf{x}, \mathbf{w})\]
Noi siamo interessati a trovare il vettore \(\mathbf{w}\) che sia migliore da un qualche punto di vista. A tale fine si definisce quindi la likelihood (verosomiglianza) dato un training set \(\mathbf{X}\) come
\[P(\mathbf{t} | \mathbf{X}, \mathbf{w}, \beta) = \prod\limits_{i = 1}^N \mathcal{N}(t_i | \mathbf{w}^T \phi(\mathbf{x}_i), \sigma^2)\]
dove con \(\mathbf{w}^T \phi(\mathbf{x}_i)\) indichiamo il valore predetto associato all'elemento \(\mathbf{x}_i\).
La corrispondente log-likelihood è quindi data da
\[\begin{split} \ln{P(\mathbf{t} | \mathbf{X}, \mathbf{w}, \beta)} &= \sum\limits_{i = 1}^N \ln{\mathcal{N}(t_i|\mathbf{w}^T \phi(\mathbf{x}_i), \sigma^2)} \\ &= N \ln{\sigma} - \frac{N}{2} \ln{(2 \pi)} - \frac{1}{\sigma^2}E_D(\mathbf{w}) \\ \end{split}\]
dove
\[E_D(\mathbf{w}) = \frac12 \sum\limits_{i = 1}^N\Big(t_i - \mathbf{w}^T \phi(x_i) \Big)^2 = \frac12 (\Phi \mathbf{w} - \mathbf{t})^T(\Phi \mathbf{w} - \mathbf{t})\]
Osserviamo quindi che massimizzare la log-likelihood in funzione di \(\mathbf{w}\) equivale a minimizzare l'espressione \(E_D(\mathbf{w})\), che è proprio la somma dei quadrati delle differenze (least squares).
Procediamo quindi impostando il gradiente della log-likelihood a \(\mathbf{0}\)
\[\begin{split} \mathbf{0} &= \frac{\partial }{\partial \mathbf{w}} \ln{P(\mathbf{t}|\mathbf{X}, \mathbf{w}, \beta)} \\ &= \sum\limits_{i = 1}^N \Big(t_i - \mathbf{w}^T \phi(x_i)\Big) \phi(x_i)^T \\ &= \sum\limits_{i = 1}^N t_i \phi(x_i)^T - \mathbf{w}^T\Bigg(\sum\limits_{i = 1}^N \phi(x_i) \phi(x_i)^T \Bigg) \\ \end{split}\]
risolvendola otteniamo le normal equations for least squares
\[\mathbf{w}_{\text{ML}} = (\Phi^T \Phi)^{-1} \Phi^T \mathbf{t}\]
Così facendo quindi a partire dal training set (formato dalla matrice \(\Phi\) e dal vettore dei valori target \(\mathbf{t}\)) siamo in grado di calcolare i coefficienti di Maximum-Likelihood del nostro modello.
Observation: Dal fatto che la funzione di partenza \(E_D(\mathbf{w})\) era una funzione quadratica, ne è conseguito che ciascuna derivata facente parte del gradiente erano tutte espressioni lineari, e quindi risolvere il gradiente essenzialmente comportava la risoluzione di un sistema lineare, che a parte casi particolari tende ad avere una e una sola soluzione, rappresentata dal vettore dei coefficenti \(\mathbf{w}_{\text{ML}}\).
Da questo risultato possiamo concludere che nel caso della regressione lineare è possibile ottenere una forma chiusa per calcolare il modello ottimo rispetto al training set. Questo tipo di risultato è molto forte, e dipende dal fatto che il modello che stiamo utilizzando è molto semplice, in quanto l'unica cosa che facciamo essenzialmente è combinare linearmente i valori delle features, o al più i valori delle funzioni base applicate alle features.
La soluzione che abbiamo appena visto per risolvere la regressione lineare ha una interpretazione geometrica molto interessante.
Consideriamo in particolare i seguenti vettori nello spazio \(N\) dimensionale \(\mathbb{R}^N\), dove \(N\) è il numero di elementi del training set:
Il vettore dei valori targer
\[\mathbf{t} = (t_1, \ldots, t_n)^T\]
Per ogni funzione base \(\phi_j\) il vettore ottenuto applicando la funzione base ai vari elementi del training set
\[\phi_j = (\phi_j(\mathbf{x}_1), \ldots, \phi_j(\mathbf{x}_N))^T\]
Fissato il modello \(\mathbf{w}\), il vettore ottenuto applicando il modello ad ogni elemento del training set
\[\mathbf{y} = (y(\mathbf{x}_1, \mathbf{w}), \ldots, y(\mathbf{x}_N, \mathbf{w})^T\]
Ora, se \(M < N\), i vettori \(\phi_1, \ldots, \phi_M\) definiscono un sottospazio \(\mathcal{S}\) di dimensione (al più) \(M\). Per definizione poi abbiamo che necessariamente il vettore \(\mathbf{y}\) deve appartenere al sottospazio \(\mathcal{S}\). Graficamente troviamo,
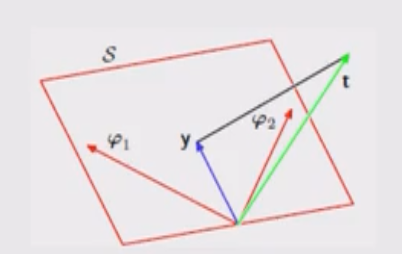
Al variare del modello \(\mathbf{w}\), il vettore \(\mathbf{y}\) sarà diverso. Fissato il vettore target \(\mathbf{t} \in \mathbb{R}^N\) e i vettori \(\phi_1, \phi_2, \ldots, \phi_M\), il modello che massimizza la massima verosimiglianza \(\mathbf{w}_{\text{ML}}\) è il modello che avvicina il più possibile il vettore \(\mathbf{y}\) al vettore \(\mathbf{t}\), ovvero il modello che minimizza la lunghezza del segmento che unisce i due vettori.
A valle di tutto il problema dell'overfitting si era discussa la possibilità di controllare la complessità del modello introducendo dei termini di regolarizzazione alla funzione di costo già esistente. In particolare quindi l'espressione che vogliamo minimizzare diventa
\[E_D(\mathbf{w}) + \lambda E_W(\mathbf{w})\]
Dove \(E_D(\mathbf{w})\) dipendend al dataset (e dai parametri del modello), mentre \(E_W(\mathbf{w})\) è il fattore di regolarizzazione che dipende solamente dai parametri del modello. Il coefficiente \(\lambda\) è detto regularization coefficient (coefficiente di regolarizzazione), e viene utilizzato per controllare la relativa importanza dei due termini.
La forma più semplice che possiamo avere per il termine di regolarizzazione è la seguente
\[E_W(\mathbf{w}) = \frac12 \sum\limits_{i = 1}^{M} w_i^2 = \frac12 \mathbf{w}^T \mathbf{w}\]
La nuova funzione di costo è quindi data da
\[E(\mathbf{w}) = \frac12 \sum\limits_{i = 1}^N \Big(t_i - \mathbf{w}^T \phi(x_i) \Big)^2 + \frac{\lambda}{2} \mathbf{w}^T \mathbf{w}\]
che in forma matriciale può essere scritta nel seguente modo
\[E(\mathbf{w}) = \frac12 (\Phi \mathbf{w} - \mathbf{y})^T (\Phi \mathbf{w} - \mathbf{y}) + \frac{\lambda}{2} \mathbf{w}^T \mathbf{w}\]
e, dato che ci troviamo in un modello molto semplice, il cui punto di minimo è dato da
\[\mathbf{w} = (\lambda \mathbf{I} + \Phi^T \Phi)^{-1} \Phi^T \mathbf{t}\]
dove il valore di \(\lambda\) è un iper parametro che deve essere scelto appositamente.
Nel termine di regolarizzazione precedente andavamo ad elevare alla potenza \(2\) ogni coefficiente del modello. Volendo generalizzare quindi possiamo introdurre un iper-parametro \(q\) ed ottenere il seguente termine di regolarizzazione
\[E_W(\mathbf{w}) = \frac{\lambda}{2} \sum\limits_{i = 1}^M |w_j|^q\]
Così facendo la funzione di costo diventa
\[E(\mathbf{w}) = \frac12 \sum\limits_{i = 1}^N \Big(t_i - \mathbf{w}^T \phi(x_i) \Big)^2 + \frac{\lambda}{2} \sum\limits_{i = 1}^M |w_j|^q\]
Al variare di \(q\) otteniamo quindi diversi comportamenti
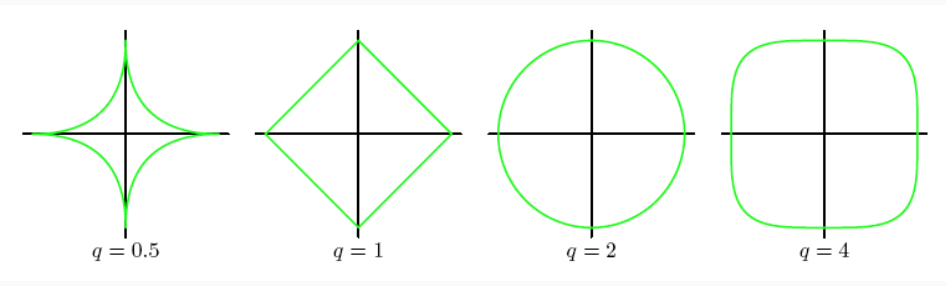
Il caso in cui \(q = 1\) è noto con il nome di lasso regression. Questo tipo di regolarizzazione tende a fornire modelli sparsi, ovvero modello in cui un elevato numero di coefficienti sono nulli. In questi modelli sparsi le features considerate sono quindi di meno.
Anche se nel caso della regressione lineare abbiamo trovato una formula chiusa per i valori \(\mathbf{w}\) che massimizzavano la likelihood, questo non è sempre il caso. In generale infatti potrebbe essere difficile il calcolo di tale valore. A tale fine si introducono dei metodi numerici iterativi per effettuare questa ottimizzazione. Questi metodi tipicamente si basano sulla gradient descent, ovvero sulla discesa del gradiente.
Consideriamo ad esempio la minimizzazione dell'espressione \(E_D(\mathbf{w})\) trovata prima. La discesa del gradiente procede in questo modo:
Si effettua un initial assignment ai coefficienti del modello \(\mathbf{w}^{(0)} = (w_0^{(0)}, w_1^{(0)}, \ldots w_D^{(0)})\) con un relativo error value iniziale di
\[E_D(\mathbf{w}^{(0)} = \frac12 \sum\limits_{i=1}^N \Big( t_i - (\mathbf{w}^{(0)})^T \phi(x_i)\Big)^2\]
In modo iterativo si modifica il valore di \(\mathbf{w}^{(i)}\) rispetto alla direzione che fornisce la steepest descent del valore di errore di \(E_D(\mathbf{w})\). In particolare, nello step \(i\) si effettua la seguente regola di update
\[w_j^{(i)} := w_j^{(i - 1)} - \eta \frac{\partial E_D(\mathbf{w})}{\partial w_j}\Big|_{\mathbf{w}^{(i-1)}}\]
Geometricamente la discesa del gradiente cerca di muoversi sempre nella direzione che ci permette di diminuire il più possibile il valore dell'errore. Ripetendo questa procedura iterativa è possibile tendere asintoticamente ad un minimo locale della funzione.
L'iper-parametro \(\eta\) è un moltiplicatore che velocizza/diminuisce il passo con cui ci muoviamo. Più alto è \(\eta\) e più il passo di aggiornamento sarà abbastanza grande, viceversa più basso è \(\eta\) e più piccolo è il passo di aggiornamento.
Voledo rappresentare la discenta del gradiente in notazione matriciale otteniamo
\[\mathbf{w}^{(i)} := \mathbf{w}^{(i - 1)} - \eta \frac{\partial E_D(\mathbf{w})}{\partial \mathbf{w}} \Big|_{\mathbf{w}^{(i-1)}}\]
Nel particolase caso in cui avevamo la funzione di costo come la funzione least squares, otteniamo la seguente espressione (sempre in notazione matriciale)
\[\mathbf{w}^{(i)} := \mathbf{w}^{(i-1)} - \eta (t_i - \mathbf{w}^{(i-1)} \phi(x_i)) \phi(x_i)\]
Per maggiori dettagli visualizzare il relativo codice python.
Ricordando invece l'approccio completamente bayesiano sotto le ipotesi gaussiane che avevamo analizzato in una lezione precedente, avevamo visto che il valore atteso della distribuzione predittiva poteva essere espresso con la seguente espressione
\[y(x) = \beta \phi(x)^T S_N \Phi^T \mathbf{t}\]
Ora, molto spesso quando siamo interessati ad una predizione puntuale, un ottimo candidato è proprio il valore atteso distribuzione. L'idea quindi è quella di utilizzare l'epressione \(y(x)\), che può essere calcolata combinando i seguenti elementi:
La matrice \(\Phi\), che è una matrice \(n \times m\) e contiene nella riga \(i\) gli elementi \(\phi_1(x_i), \ldots, \phi_m(x_i)\).
\(\phi(x)\) è un vettore colonna di \(m\) componenti, che rappresenta il punto in cui viene mappato \(x\) dalle base functions. Dunque \(\phi(x)^T\) è un vettore riga.
\[\phi(x)^T = \begin{pmatrix} \phi_1(x) & \phi_2(x) & \ldots & \phi_m(x) \end{pmatrix}\]
La matrice \(S_N\) per costruzione è una matrice quadrata \(m \times m\) ed è definita come segue
\[S_N = \alpha I + \beta \sum\limits_{i = 1}^n x x^T\]
Notiamo poi che è possibile riscrivere l'espressione \(y(x)\) come una somma nel seguente modo
\[y(x) = \sum_{i = 1}^N \beta \phi(x)^T S_N \phi(x_i) t_i\]
Il valore predetto dunque è ottenuto da una combinazione lineare dei valori target associati agli elementi del training set, dove il valore target \(t_i\) è pesato dal valore \(\beta \phi(x)^T S_N \phi(x_i)\). In formula,
\[y(x) = \sum\limits_{i = 1}^n \kappa(x, x_i) t_i\]
Dove la funzione di pesatura
\[\kappa(x, x') = \beta \phi(x)^T S_N \phi(x')\]
è detta equivalent kernel, o linear smoother, e una volta fissato il training set è funzione sia del punto in cui si vuole fare la predizione e di un punto del training set rispetto al quale la predizione è nota.
Questo nuovo modo di rappresentare la predizione è completamente diverso da quello che abbiamo fino a questo punto. In particolare troviamo due metodi di esprimere la predizione in un contesto di apprendimento supervisionato
Impostazione primale: si utilizzare il training set \((\Phi, \mathbf{t})\) per derivare un insieme di coefficienti \(W^*\) e dato un punto \(x\) la predizione veniva ottenuta ponendo \(y(x) = (W^*)^T x\).
Impostazione duale: La predizione viene effettuata sempre a partire da predizioni corrette degli elementi del training set, ma questa volta non passando a dei coefficienti espliciti, bensì sulla base dell'espressione \(\kappa(x, x_i)\) in cui compare sia il training set e sia il punto in cui deve essere effettuata la predizione.
La funzione kernel equivalente \(\kappa(x, x')\) può essere interpretata in modo approssimativo come una funzione di vicinanza, ovvero una funzione che determina quanto l'elemento \(x\) e l'elemento \(x'\) in qualche modo sono vicini, in modo tale da capire quanto il valore del target di \(x'\) è rilevante alla fine della predizione del valore associato ad \(x\).
Questa caratteristica della funzione kernel dipende dalle funzioni base \(\phi_1, \ldots \phi_m\) utilizzate.