ML - 19 - Support Vector Machines I
Lecture Info
Date:
Lecturer: Giorgio Gambosi
Slides: (ml_10_svm-slides.pdf)
In questa lezione abbiamo introdotto le idee fondamentali dietro le support vector machines andando a definire i concetti di margine funzionale e margine geometrico. Infine, abbiamo terminato la lezione introducendo brevemente l'idea dietro alla teoria della dualità e di come la andremmo ad utilizzare per risolvere il nostro problema di ottimizzazione.
1 Main Idea
Le support vector machines sono ulteriore modello di classificazione lineare che ci permettono di definire degli iperpiani di separazione tra le classi.
L'idea di fondo delle SVMs infatti è quella di cercare l'iperpiano "migliore" che separa le classi nello spazio delle features rispetto ad una misura di separazione. Se questo non può essere fatto in modo ottimale (problema già incontrato studiando il percettrone), il problema viene approciato in due modi alternativi:
Da un lato si cerca di allentare, rilassando, la definizione di "separazione" utilizzata per misurare la qualità dell'iperpiano ottenuto. In particolare quindi si ammettono degli errori nella classificazione dell'iperpiano andando però ad associare un costo a questa situazione.
Dall'altro lato si cerca di aumentare lo spazio delle features in modo tale da rendere la separazione più plausibile da calcolare.
Consideriamo la seguente figura
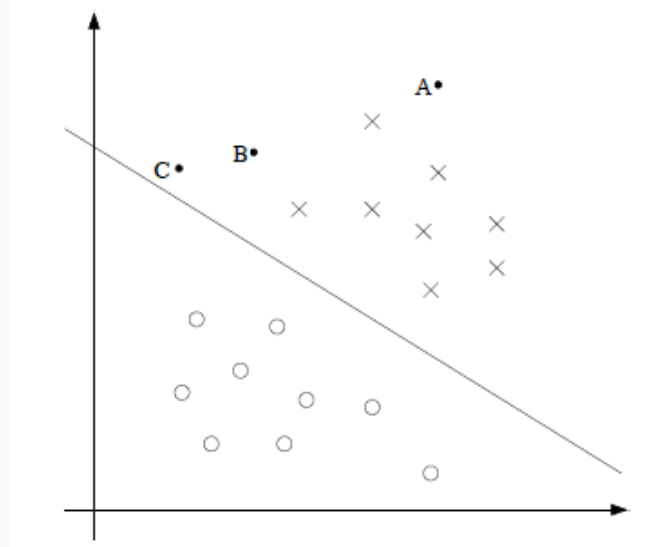
e sia \(C_1\) la classe dei punti \(\text{X}\), mentre \(C_2\) è la classe dei punti \(\text{O}\). Notiamo che per come stanno le cose, la confidenza con cui assegniamo il punto \(\text{A}\) alla classe \(C_1\) è molto più alta di quella con cui assegniamo i punti \(\text{B, C}\) alla classe \(C_1\).
Detto altrimenti, tanto più un punto è lontano dall'iperpiano di separazione, tanto maggiore è la confidenza con cui classifichiamo quel punto.
Tutto l'approccio dietro alle SVM è sviluppato a partire da questa idea. Un SVM infatti è un classificatore che cerca un iperpiano di separazione tale che la distanza di tutti i punti del training set dall'iperpiano di separazione sia la più grande possibile.
2 Binary Classifiers
Consideriamo quindi un classificatore binario che per ogni elemento \(x\) fornisce un valore \(y \in \{-1, 1\}\) in cui assumiamo che se \(y = -1\) allora \(x \in C_0\), e se \(y = 1\) allora \(x \in C_1\).
Assumiamo poi che la classificazione viene effettuata utilizzando un particolare modello lineare generalizzato della forma
\[h(x) = g(\mathbf{w}^T \phi(x) + w_0)\]
dove \(\phi(x) = (\phi_1(x), \ldots, \phi_r(x))\) e
\[g(z) = \begin{cases} 1 & z \geq 0 \\ -1 & z < 0 \\ \end{cases}\]
questo in particolare significa che per classificare l'elemento \(x\) non andiamo a stimare la probabilità che \(x\) appartenga alla classe, ovvero \(P(C_i|x)\). Ovvero le SVM non sono un modello di classificazione probabilistica.
3 Optimal Margin Classifiers
Al fine di costruire un classificatore binario tramite le SVM dobbiamo introdurre due concetti fondamentali: i margini funzionali e i margini geometrici.
3.1 Functional Margins
Assumiamo di avere un iperpiano di separazione \((\mathbf{w}, w_0)\) per un dato training set, e consideriamo un elemento \((x_i, t_i\)) di tale training set. Si definisce quindi la seguente quantità, che prende il nome di margine funzionale, o functional margin
\[\overline{\gamma}_i = t_i(\mathbf{w}^T \phi(x) + w_0)\]
Dato che \(\mathbf{w}^T \phi(x) + w_0\) rappresenta la distanza dell'elemento dall'iperpiano preso in considerazione e che la distanza è col segno, se il punto è ben classificato il valore del margine funzionale sarà positivo \(\overline{\gamma}_i > 0\).
L'intuizione inoltre è che più alto è il valore di \(\overline{\gamma}_i\) e più alta sarà la nostra confidenza per quella particolare predizione.
Dato un training set \(\mathcal{T} = \{(x_1, t_1, \ldots, (x_n, t_n)\}\) il margine funzionale di \((\mathbf{w}, w_0)\) rispetto a \(\mathcal{T}\) è definito come il minimo margine funzionale tra tutti gli elementi in \(\mathcal{T}\). In formula,
\[\overline{\gamma} = \underset{i}{\min{\overline{\gamma}_i}}\]
Osserviamo come tale grandezza dipende dal particolare iperpiano scelto. Cambiando l'iperpiano di separazione andremmo anche a cambiare i vari margini di separazione, e dunque anche il minimo fra questi ultimi.
3.2 Geometric Margin
A partire dal margine funzionale definiamo poi il margine geometrico, o geometric margin. Il margine geometrico rispetto ad un elemento del training set \((x_i, t_i)\) viene indicato con \(\gamma_i\) ed è definito come il prodotto tra \(t_i\) e la distanza tra \(x_i\) e l'iperpiano di separazione opportunamente scalata.
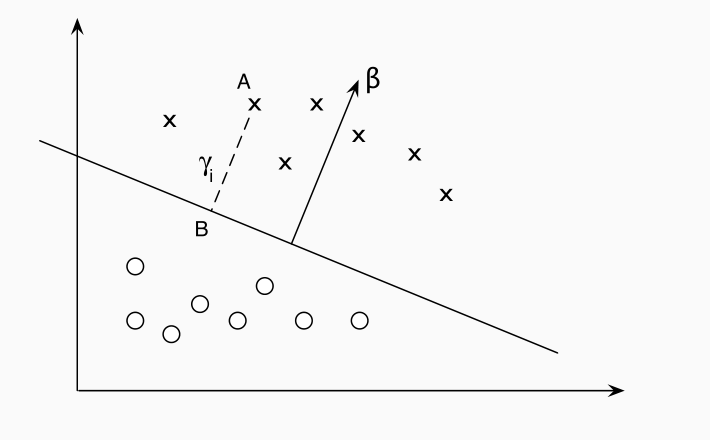
A differenza del margine geometrico, che è unico una volta che fissiamo l'elemento del training set e l'iperpiano di separazione, il margine funzionale, sempre fissati gli stessi elementi, non è unico, in quanto mi basta scalare l'iperpiano per una costante \(c\), ottenendo il nuovo iperpiano \((c \mathbf{w}, c w_0)\), e per questo iperpiano avrò dei diversi margini funzionali per ogni elemento del training set. In altre parole, il margine geometrico rappresenta una versione normalizzata del margine funzionale.
Infatti, dato che la distanza di un punto \(\overline{x}\) dall'iperpiano \(\mathbf{w}^T x = 0\) è \(\frac{\mathbf{w}^T \overline{x}}{||\mathbf{w}||}\), ne segue che
\[y_i = t_i \Bigg( \frac{\mathbf{w}^T}{||\mathbf{w}||} \phi(x) + \frac{w_0}{||\mathbf{w}||} \Bigg) = \frac{\overline{\gamma}_i}{||\mathbf{w}||}\]
Da questo segue che, a differenza del margine funzionale, il margine geometrico \(\gamma_i\) è invariante rispetto alla scalatura dei parametri in quanto
\[\begin{split} \overline{\gamma}_i &= t_i(c \mathbf{w}^T \phi(x) + c w_0) = c t_i(\mathbf{w}^T \phi(x) + w_0) \\ \\ \gamma_i &= t_i \Bigg( \frac{c\mathbf{w}^T}{||c\mathbf{w}||} \phi(x) + \frac{cw_0}{||c\mathbf{w}||} \Bigg) = t_i \Bigg( \frac{\mathbf{w}^T}{||\mathbf{w}||} \phi(x) + \frac{w_0}{||\mathbf{w}||} \Bigg) \\ \end{split}\]
Esattamente come nel caso precedente, il margine geometrico di un training set \(\mathcal{T} = \{(x_1, t_1), \ldots, (x_n, t_n)\}\) è definito come il più piccolo marigne geometrico tra tutti gli items \((x_i, t_i)\).
\[y = \underset{i}{\min{\gamma_i}}\]
3.2.1 Maxium Margin Hyperplanes
Una utile interpretazione del margine geometrico è la seguente: possiamo considerare il valore \(\gamma\) come la metà della larghezza della più grande striscia centrata nell'iperpiano \(\mathbf{w}^T \phi(x) + w_0 = 0\) che non contiene i punti \(x_1, \ldots, x_n\).
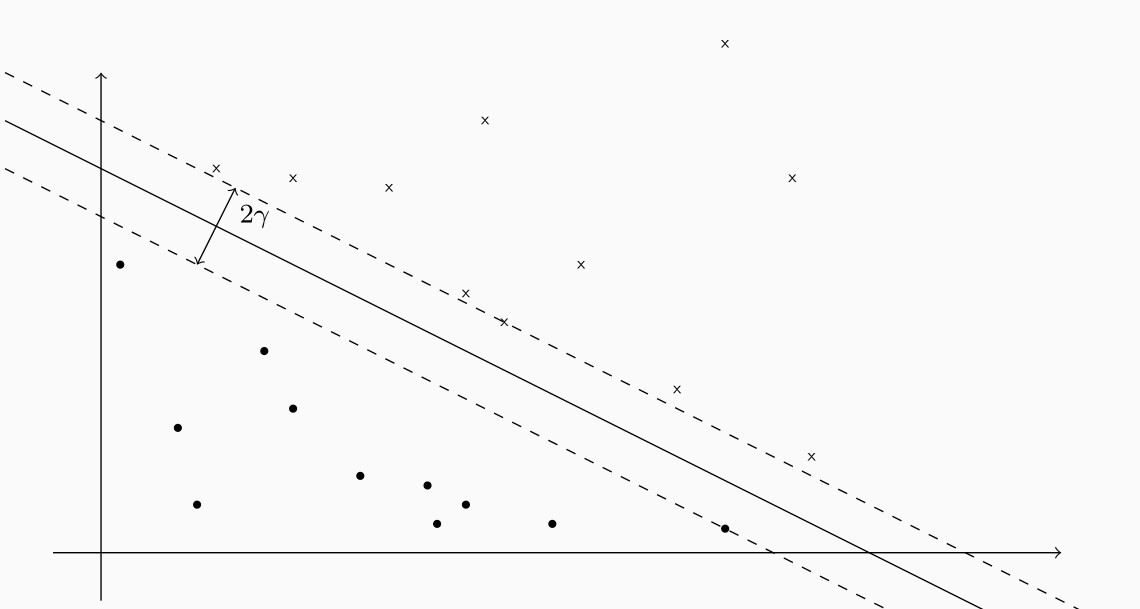
Gli iperpiani che si trovano nei confini di questa striscia, ciascuno a distanza \(\gamma\) dall'iperpiano e almeno almeno uno di questi passante per qualche punto \(x_i\) sono detti iperpiani di massimo margine, o maximum margin hyperplanes.
3.3 Classification Details
In generale per ogni elemento \((x, t)\) troviamo che:
Se \(t(\mathbf{w}^T \phi(x) + w_0) > 1\), allora \(\phi(x)\) è nella regione che corrisponde alla sua classe, al di fuori della striscia di margine.
Se \(t(\mathbf{w}^T \phi(x) + w_0) = 1\), allora \(\phi(x)\) è nella regione che corrisponde alla sua classe, su un un iperpiano di massimo margine.
Se \(0 < t(\mathbf{w}^T \phi(x) + w_0) < 1\), allora \(\phi(x)\) si trova nella regione che corrisponde alla sua classe, all'interno della striscia di margine.
Se \(t(\mathbf{w}^T \phi(x) + w_0) = 0\), allora \(\phi(x)\) si trova sull'iperpiano di separaizone.
Se \(-1 < t(\mathbf{w}^T \phi(x) + w_0) < 0\), allora \(\phi(x)\) si trova nella regione che corrisponde all'altra clase, all'interno della striscia di margine.
Se \(t(\mathbf{w}^T \phi(x) + w_0) = -1\), allora \(\phi(x)\) si trova nella regione che corrisponde all'altra clase, su un un iperpiano di massimo margine.
Se \(t(\mathbf{w}^T \phi(x) + w_0) < -1\), allora \(\phi(x)\) si trova nella regione che corrisponde all'altra clase, al di fuori della striscia di margine.
3.4 Computing The Optimal Margin
Consideriamo un training set \(\mathcal{T}\) e assumiamo che le classi siano linearmente separabili nel training set, ovvero che esistono infiniti iperpiani che separano gli elementi in \(C_1\) rispetto a quelli in \(C_2\).
Tra tutti questi iperpiani, l'idea è quella di trovare l'iperpiano che separa le due classi (se esiste) e che massimizza il margine geometrico \(\gamma\) rispetto a \(\mathcal{T}\). Ricordiamo infatti che andando a massimizzare questo margine geometrico stiamo anche massimizzando la confidenza con cui andiamo a classificare ogni elemento del training set. Il nostro problema si riduce quindi al seguente problema di ottimizzazione
\[\underset{\mathbf{w}, w_0}{\max} \,\,\, \gamma\]
dove,
\[\gamma_i = \frac{t_i}{||\mathbf{w}||}(\mathbf{w}^T \phi(x) + w_0) \geq \gamma, \,\,\,\,\, i = 1, \ldots, n\]
Un modo equivalente per esprimere il vincolo è il seguente
\[t_i(\mathbf{w}^T \phi(x) + w_0) \geq \gamma || \mathbf{w} || \,\,\,\,\, i = 1, \ldots, n\]
Come già osservato, se tutti i parametri sono scalati da una qualsiasi costante \(c\), tutti i margini geometrici \(\gamma_i\) tra gli elementi e l'iperpiano considerato non cambiano. Possiamo sfruttare questo grado di libertà per introdurre il seguente vincolo
\[\gamma = \underset{i}{\min} \,\,\, t_i(\mathbf{w}^T \phi(x) + w_0) = 1\]
questo vincolo è rispettato assumendo \(||\mathbf{w} || = \frac{1}{\gamma}\), che corrisponde a considerare una scala di misura in cui il massimo margine ha ampiezza \(2\). Per ogni elemento del training \(x_i, t_i\) troviamo quindi il seguente vincolo
\[\gamma_i = t_i(\mathbf{w}^T \phi(x) + w_0) \geq 1\]
I punti che si trovano esattamente a distanza \(1\) dall'iperpiano vengono detti attivi. Formalmente un punto è attivo se vale la seguente uguaglianza
\[t_i(\mathbf{w}^T \phi(x) + w_0) = 1\]
se tale uguaglianza non vale, il punto è detto inattivo. Per come è stato definito \(\gamma\), deve necessariamente esistere almeno un punto attivo.
Il problema di ottimizzazione diventa quindi il seguente
\[\underset{\mathbf{w}, w_0}{\max} \,\,\, \gamma = \underset{\mathbf{w}, w_0}{\max} \,\,\, ||\mathbf{w}||^{-1}\]
dove,
\[t_i(\mathbf{w}^T \phi(x) + w_0) \geq 1 \,\,\,\, i = 1, \ldots, n\]
Notando poi che massimizzare \(||\mathbf{w}||^{-1}\) è equivalente a minimizzare \(||\mathbf{w}||^2\) (sarebbe equivalente pure minimizzare la norma \(||\mathbf{w}||\), ma preferiamo il quadrato della norma in quanto è smooth everywhere) riscriviamo il nostro problema come segue
\[\begin{split} &\underset{\mathbf{w}, w_0}{\min} \,\,\, \frac12 ||\mathbf{w}||^2 \\ &\text{where } \,\,\, t_i(\mathbf{w}^T \phi(x) + w_0) \geq 1 \,\,\,\,\, i = 1,\ldots, n \\ \end{split}\]
Notiamo che questa è un problema di ottimizzazione di tipo quadratico e convesso (convex quadratic), in quanto la funzione obiettivo è una funzione convessa e il dominio delle possibili soluzioni forma un poliedo convesso (convex polyhedron) che è l'intersezione di semi spazi definiti da iperpiani.
3.5 Duality
Dalla teoria delle ottimizzazioni (optimization theory) segue che data la struttura del nostro problema, ovvero il fatto che abbiamo vincoli lineari e una funzione convessa, esiste una formulazione duale del problema, e che l'ottimo del problema duale è uguale alla soluzioone del problema originale (detto problema primale).
L'idea è quindi quella di partire dal nostro problema primale \(P\) e costruire il problema duale \(P^{'}\), risolvere quest'ultimo e, a partire dalla soluzione del problema duale, costruirci una soluzione del problema primale.