ML - 21 - Support Vector Machines III
Lecture Info
Date:
Lecturer: Giorgio Gambosi
Slides: (ml_10_svm-slides.pdf)
In questa lezione abbiamo discusso brevemente alcune limitazioni dal punto di vista computazionale rispetto a quanto visto per il training delle SVM. Abbiamo poi parlato in generale delle loss functions e dei regularization terms nel contesto della classificazione e abbiamo terminato la lezione esprimendo il training di un modello SVM come un processo di discesa del gradiente.
1 Computational Issues
Dal punto di vista computazionale, l'apprendimento delle SVM tramite soluzione di un problema di ottimizzazione quadratica convessa risulta essere \(O(n^3)\), che anche se è una quantità polinomiale, in pratica risulta essere abbastanza pesante, specialmente al crescere del size del training set.
Per cercare di migliorare le performance di addestramento ci sono due approcci principali:
Una prima idea è quella di risolvere più efficientemente il problema di ottimizzazione quadratica convessa, accettando eventuali approssimazioni.
Un altro approccio consiste nel dare una caratterizzazione equivalente ma diversa delle SVM da quella appena data che però evita direttamente la risoluzione di un problema quadratico convesso. Ad esempio potremmo trovare una caratterizzazione che utilizza il metodo gradient descent per addestrare il modello. In questo caso però necessitiamo di definire una loss function e di calcolare il suo gradiente.
2 Loss Functions in Classification
Andiamo adesso a considerare una serie di loss functions, ovvero di funzioni che calcolano l'errore del modello, nell'ambito della classificazione, limitandoci alla trattazione del caso binario, in quanto contiene tutti i concetti di interesse.
Le domande importanti che dobbiamo rispondere in questo contesto sono le seguenti:
Come possiamo modificare il nostro problema di ottimizzazione, ovvero come possiamo cambiare la funzione di costo, in modo tale da poter utilizzare degli algoritmi efficienti in grado di risolverlo?
Quali sono dei buoni componenti di regolarizzazione \(R(\mathbf{w}, b)\) rispetto agli iperpiani che comunque mi permettono di risolvere il problema di ottimizzazione finale in modo efficiente?
2.1 0/1 Loss
La funzione di loss più "naturale" è quella che conta il nmero di elementi mal classificati. In formula
\[\underset{\mathbf{w}, b}{\text{argmin}} \,\, \sum\limits_{i = 1}^n \mathbf{1}\Big[t_i(\mathbf{w}^T x_i + b) < 0 \Big] \]
graficamente la funzione indicatrice può essere visualizzata come segue
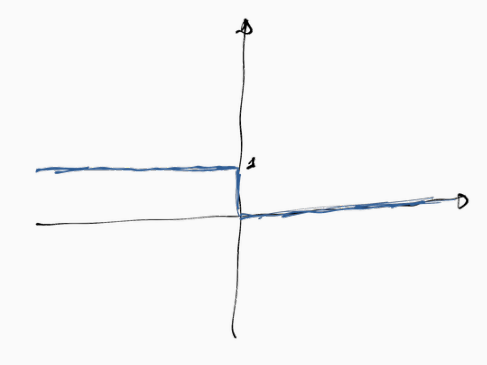
Rispetto a questa funzione andiamo quindi a considerare due casi separati:
Se il minimo della funzione è \(0\), ovvero quando tutti gli elementi sono ben classificati e quindi le classi sono separabili linearmente, allora il Percettrone risce a trovare la soluzione ottimale (anche utilizzando una loss function diversa).
Se il minimo della funzione è \(> 0\), ovvero se le classi non sono linearmente separabili, l'utilizzo del Percettrone non ci permette di ottenere una qualsiasi soluzione, in quanto il problema risulta essere NP-hard anche solo da approssimare, almeno fino ad una piccola costante.
2.1.1 Regularization
Ricordiamo che il fatto stesso di trovare l'iperpiano di separazione ottimo potrebbe portare problemi di overfitting. Per cercare di marginare questa tipologia di problematiche l'idea è quella di introdurre un regularization term, ovvero un termine di regolarizzazione.
La struttura della funzione di costo viene quindi modificata come segue
\[\underset{\mathbf{w}, b}{\text{argmin}} \,\, \sum\limits_{i = 1}^n \mathbf{1}\Big[t_i(\mathbf{w}^T x_i + b) < 0 \Big] + \lambda R(\mathbf{w}, b)\]
dove \(\lambda\) è un iperparametro che controlla il fattore di regolarizzazione.
2.1.2 Problems
La funzione di loss 0/1 presenta i seguenti problemi:
È costante la maggior parte del tempo, ovvero se prendo l'iperpiano che separa le classi e gli sposto di poco la sua posizione, il valore della loss function non cambia, o cambia di molto poco.
Alcune volte però varia in modo brusco.
Queste due motivazioni ci portano a dire che la 0/1 loss non è una funzione smooth.
2.2 Surrogate Smooth Loss Functions
L'idea è quindi quella di presentare alcune loss functions che sono simili alla 0/1 loss ma che allo stesso tempo sono più gestibili della 0/1 loss. Un esempio di tale funzione è riportata a seguire, ed è una funzione logistica messa al contrario.
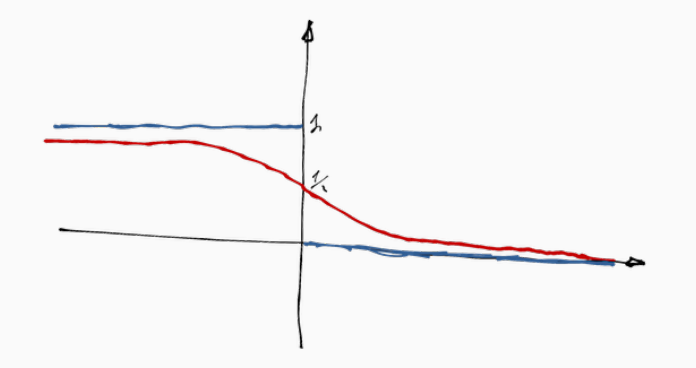
Utilizzando una funzione del genere notiamo le seguenti cose:
I punti che vengono classificati male non pesano nello stesso modo nella funzione loss. Pesano almeno \(0.5\), ma quelli più vicini all'iperpiano di separazione pesano di meno piuttosto a quelli più lontani.
Lo stesso vale per i punti ben classificati, nel senso che i punti ben classificati, ma di poco, pesano di più, mentre quelli ben classificati ma di tanto pesano di meno.
Con questi accorgimenti abbiamo che la loss varia in modo continuo rispetto alla distanza dall'iperpiano, e questo ci permette di utilizzare le derivate per lavorare con queste funzioni.
2.3 Convex Loss Functions
Oltre ad avere una loss function smooth, che ci permette appunto di poter utilizzare le derivate per studiare l'andamento della stessa, un'altra caratteristica utile da avere è la convessità.
Graficamente una funzione convessa ha la seguente forma
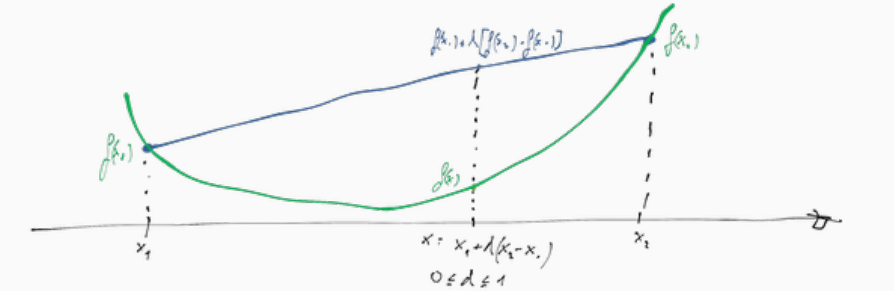
Come è possibile vedere dal grafico, dati due punti \(x_1, x_2\), e dato un terzo punto \(x\) compreso tra questi due, deve valere che il valore assunto dalla retta passante per i due punti \(f(x_1)\) e \(f(x_2)\) nel punto \(x\) deve essere superiore rispetto al valore assunto dalla funzione in quel punto, ovvero \(f(x)\).
Analiticamente questa condizione può essere verificata guardando la seconda derivata, che deve essere sempre non negativa, e quindi che può avere (al più) un punto di minimo.
Come conseguenza di questo, trovare il minimo locale corrisponde a trovare il minimo globale. Inoltre, dato che la prima derivata è monotona non-decrescete, in un qualunque punto il gradiente punta nella direzione del minimo locale (e quindi del minimo globale).
Ed è proprio per questo che è molto utile lavorare con funzioni convesse: perché con questo tipo di funzione seguendo il gradiente arriviamo sempre al minimo globale.
2.4 Convex Surrogate Loss Functions
Mettendo assieme le ultime due caratteristiche discusse, siamo interessati a funzioni che
Approssimano da sopra la funzione 0/1 loss, ovvero che l'errore ritornatci dalla funzione è sempre maggiore dell'errore ritornato dalla 0/1 loss.
Sono convesse, e quindi hanno un solo minimo locale che corrisponde anche al minimo globale.
Sono smooth, e quindi ci permettono di utilizzare le derivate per calcolare il punto di minimo.
Sia \(y = \mathbf{w}^T x + b\) il valore predetto e \(t\) il valore target. Seguono alcune delle più famose funzioni di costo:
0/1 loss
\[L(t, y) = \mathbf{1}\Big[y \cdot t \leq 0 \Big]\]
Squared
\[L(t, y) = (t - y)^2\]
Logistic
\[L(t, y) = \frac{1}{\log 2} \log{(1 + e^{-yt})}\]
Exponential
\[L(t, y) = e^{-yt}\]
Hinge
\[L(t, y) = \max{(0, \,\,\, 1 - yt)}\]
Un grafico complessivo in cui è possibile vedere il comportamento di tutte queste funzioni è il seguente
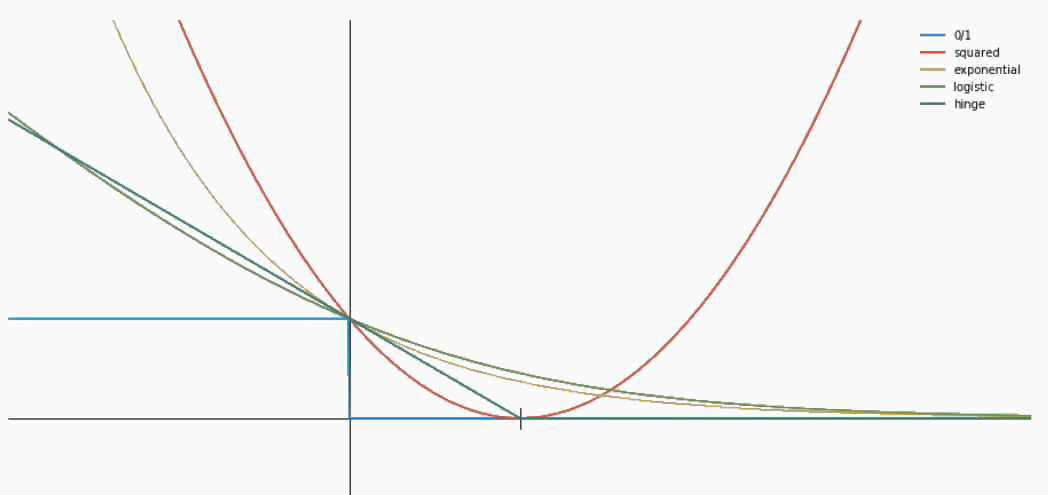
come possiamo vedere, funzioni diverse ci danno costi diverse all'aumentare/diminuire della distanza del punto dall'iperpiano di separazione.
2.5 Hinge Loss
La funzione Hinge loss \(L_H(y, t) = \max{(0, \,\, 1 - ty)}\) non è differenziaible rispetto a \(y\) quando \(ty = 1\). Abbiamo quindi
\[\frac{\partial }{\partial y} L_H = \begin{cases} -t & ty < 1 \\ 0 & ty > 1 \\ \text{undefined} & ty = 1 \\ \end{cases}\]

Per applicare il metodo della gradient descent alla funzione hinge notiamo che dal fatto che \(y = \mathbf{w}^T x + b\), abbiamo
\[\begin{split} \Delta_{\mathbf{w}} y &= \mathbf{x} \\ \\ \frac{\partial y}{\partial b} &= 1 \\ \end{split}\]
e quindi
\[\Delta_{\mathbf{w}} L_H = \begin{cases} -tx & t(\mathbf{w}^T x + b) < 1 \\ 0 & t(\mathbf{w}^T x + b) > 1 \\ \text{undefined} & t(\mathbf{w}^T x + b) = 1 \\ \end{cases}\]
\[\frac{\partial}{\partial b} L_H = \begin{cases} -t & t(\mathbf{w}^T x + b) < 1 \\ 0 & t(\mathbf{w}^T x + b) > 1 \\ \text{undefined} & t(\mathbf{w}^T x + b) = 1 \\ \end{cases}\]
dato che il gradiente non è definito ovunque, l'idea è quella di utilizzare una tecnica surrogata che è la tecnica del subgradiente.
2.5.1 Subgradient
Se abbiamo a che fare con una funzione convessa \(f\) (come nel caso della hinge loss), nei punti in cui esiste la derivata, la funzione gradiente \(\Delta(x)\) ci fornisce sempre una funzione che da un lower bound a \(f\). In formula,
\[f(x^{'}) \leq f(x) + \Delta(x)(x - x^{'})\]
Graficamente,

Consideriamo adesso un punto singolare \(x\) di \(f\) in cui non possiamo calcolare la derivata. Invece di considerare il gradiente, ovvero la derivata, consideriamo una qualsiasi funzione che passa per quel punto e che mi da sempre un lower bound rispetto alla funzione originaria. Queste funzioni sono dette subgradient (subgradiente), e un subgradiente è indicata con \(\overline{\Delta}(x)\) ed è tale che
\[f(x^{'}) \geq f(x) + \overline{\Delta}(x)(x - x^{'})\]
Per la hinge loss troviamo la seguente situazione
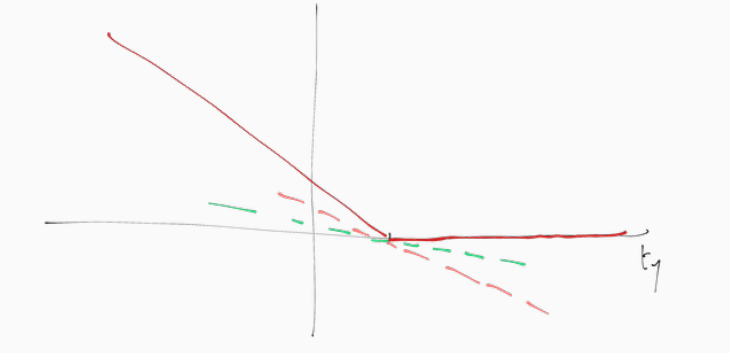
Possiamo quindi scegliere l'asse orizzontale come subgradiente da utilizzare, ovvero assumiamo che \(\frac{\partial L_h}{\partial y} = 0\) quando \(ty = 1\). Così facendo troviamo quindi
\[\overline{\Delta}_{\mathbf{w}} L_H = \begin{cases} -tx & t(\mathbf{w}^T x + b) < 1 \\ 0 & t(\mathbf{w}^T x + b) \geq 1 \\ \end{cases}\]
\[\frac{\overline{\partial}}{\partial b} L_H = \begin{cases} -t & t(\mathbf{w}^T x + b) \leq 1 \\ 0 & t(\mathbf{w}^T x + b) \geq 1 \\ \end{cases}\]
Utilizzanda questo subgradiente siamo quindi in grado di applicare la discesa del gradiente.
2.5.2 Perceprton
Notiamo come la hinge loss traslata di \(-1\) equivale alla segeunte funzione
\[L_H(\mathbf{w}, b, x, t) = \max{(0, \,\, -y(\mathbf{w}^T x +b))}\]
graficamente,
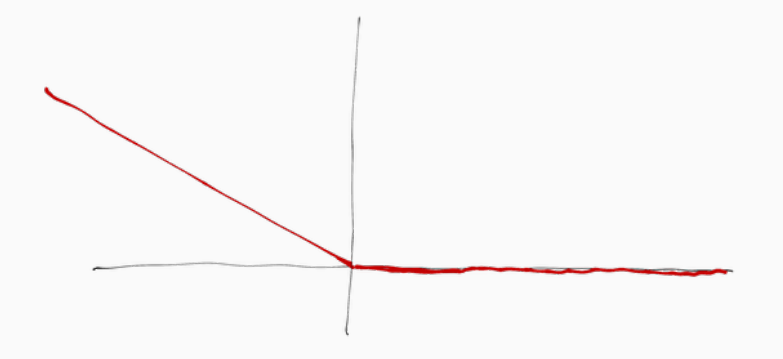
che è proprio la funzione loss che abbiamo visto nel modello del percettrone. Questa funzione loss non è un upper bound alla funzione 0/1 loss, e quindi per punti che sono classificati male questa funzione ci da un costo minore della 0/1 loss.
2.6 Logistic Loss
La logistic loss è stata definita come segue
\[L_l(t, y) = \frac{1}{\log{2}} \log{(1 + e^{-ty})}\]
è possibile vedere che minimizzare la logistic loss è equivalente a minimizzare la cross entropy nel contesto della logistic regression
\[t\log{y} + (1 - t)\log{(1 - y)}\]
Osservando infatti i casi in cui \(t = 1\) e \(t = -1\) troviamo che
\[L_t(\mathbf{w}, b, t, x) \propto \begin{cases} -\log{(\sigma(\mathbf{w}^T x + b))} &= -\log{(p(C_1|x))} & \,\,\,,\,\,\,t = 1 \\ -\log{(1 - \sigma(\mathbf{w}^T x + b))} &= -\log{p(C_0|x)} & \,\,\,,\,\,\,t = - 1\\ \end{cases}\]
che è lo stesso risutlato di quello ottenuto dalla cross entropy nei casi in cui \(t=1\) e \(t=0\)
\[\begin{cases} -\log{(\sigma(\mathbf{w}^T x + b))} &= -\log{(p(C_1|x))} & \,\,\,,\,\,\,t = 1 \\ -\log{(1 - \sigma(\mathbf{w}^T x + b))} &= -\log{p(C_0|x)} & \,\,\,,\,\,\,t = 0\\ \end{cases}\]
3 Regularization Terms
Alcuni dei più comuni termini di regolarizzazione sono i seguenti, tutti definiti in funzione di \(\mathbf{w}\)
0 norm
\[R_0(\mathbf{w}) = \mathbf{1}\Big[w_i \neq 0 \Big]\]
1 norm (lasso regression)
\[R_1(\mathbf{w}) = \sum\limits_{i = 1}^d |w_i|\]
2 norm (ridge regression)
\[R_2(\mathbf{w}) = \frac12 \sum\limits_{i = 1}^d w_i^2\]
p norm
\[R_p(\mathbf{w}) = \Big(\sum\limits_{i = 1}^d |w_i|^p\Big)^{1/p}\]
Mettendo insieme una loss function più un regularization term siamo in grado di ottenere anche i seguenti metodi:
Ridge regression: squared loss and \(R_2\) regularization.
Lass regression: squared loss and \(R_1\) regularization.
Regularized logistic regression: logistic loss and \(R_2\) regularization.
Perceprton: hinge loss, no regularization.
4 SVM and Gradient Descent
Ricordiamo che nel caso generale (in cui non assumiamo che le classi siano separabili linearmente), la funzione di costo da minimizzare nel modello SVM era definita nel seguente modo
\[\begin{split} &\underset{\mathbf{w}, \,\, w_0, \,\, \mathbf{\xi}}{\min} \,\,\, \frac12 \mathbf{w}^T \mathbf{w} + C \cdot \sum\limits_{i = 1}^n \xi_i \\ &\text{where } \\ & \, t_i(\mathbf{w}^T \phi(x_i) + w_0) \geq 1 - \xi_i & \,\,\,\,\, i = 1,\ldots, n \\ & \, \xi_i \geq 0 & \,\,\,\,\, i = 1,\ldots, n \\ \end{split}\]
Dato un valore dei coefficienti \(\mathbf{x}, w_0\), la variabile di slack \(\xi_i\) è minimizzata nel seguente modo
\[\xi_i = \begin{cases} 0 & \,\,\,,\,\,\, t_i(\mathbf{w}^T \phi(x_i) + w_0) \geq 1 \\ 1 - t_i(\mathbf{w}^T \phi(x_i) + w_0) & \,\,\,,\,\,\, \text{otherwise} \\ \end{cases}\]
Il valore ottimale di \(\xi_i\) corrisponde quindi alla hinge loss del corrispondente elemento. In formula,
\[L_H(\mathbf{w}, w_0, x_i, t_i) = \max{(0, \,\,\, 1 - t_i(\mathbf{w}^T \phi(x_i) + w_0))}\]
Possiamo quindi definire il costo della funzione da minimizzare nel seguente modo
\[\begin{split} C(\mathbf{w}) &= \frac{\alpha}{2} \mathbf{w}^T \mathbf{w} + \sum\limits_{i = 1}^n L_H(\mathbf{w}, w_0, x_i, t_i) \\ &= \sum\limits_{i = 1}^n L_H(\mathbf{w}, w_0, x_i, t_i) + R_2(\mathbf{w}) \\ \end{split}\]
da questo segue che SVM corrisponde al caso hinge loss con regolarizzazione ridge.
Il subgradiente in questo caso ha la seguente forma
\[\overline{\Delta}_w = \mathbf{w} - \sum\limits_{x_i \in L}t_i \phi(x_i)\]
dove \(x_i \in L\) se e solo se \(t_i(\mathbf{w}^T \phi(x_i) + w_0) < 1\). L'iterazione della discesa del gradiente è dunque dettata dalla seguente equazione
\[\mathbf{w}^{(r+1)} = \mathbf{w}^{(r)} - \alpha \mathbf{w}^{(r)} + \alpha \sum\limits_{x_i \in L} t_i \phi(x_i)\]