Kernel Methods
Date:
Author: Leonardo Tamiano
Table of Contents:
Nel presente documento è riportata la trattazione del metodo kernel per gestire casi di classificazione binaria in cui i dati non sono linearmente separabili. Prima di leggere questo si consiglia la lettura del documento sulle SVMs.
Alla fine della discussione sulle SVMs avevamo approcciato il problema di gestione dei dati non linearmente separabili tramite il rilassamento del problema di ottimizzazione e l'introduzione delle slack variables.
Esiste però un altro approccio che è possibile utilizzare per cercare di classificare dati che inizialmente non sono linearmente separabili: cambiare lo spazio di rappresentazione tramite una funzione (eventualmente non-lineare) \(\Phi\).
Possiamo dare un'intuizione grafica di quanto descritto nel seguente modo:
Consideriamo il seguente spazio di input, in cui si vede chiaramente che i dati non sono linearmente separabili.
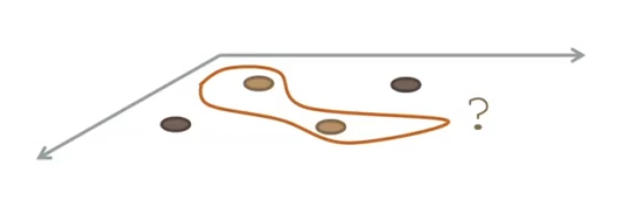
Andiamo adesso ad applicare la trasformazione \(\Phi\) per proiettare i dati in un nuovo spazio, con più dimensioni.
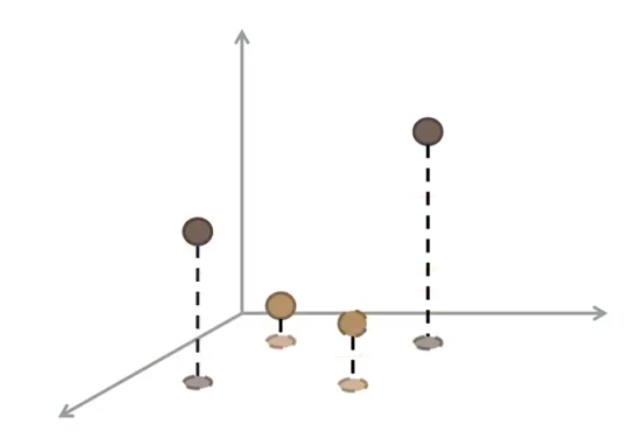
È possibile vedere che, nel nuovo spazio, i dati diventano nuovamente linearmente separabili.
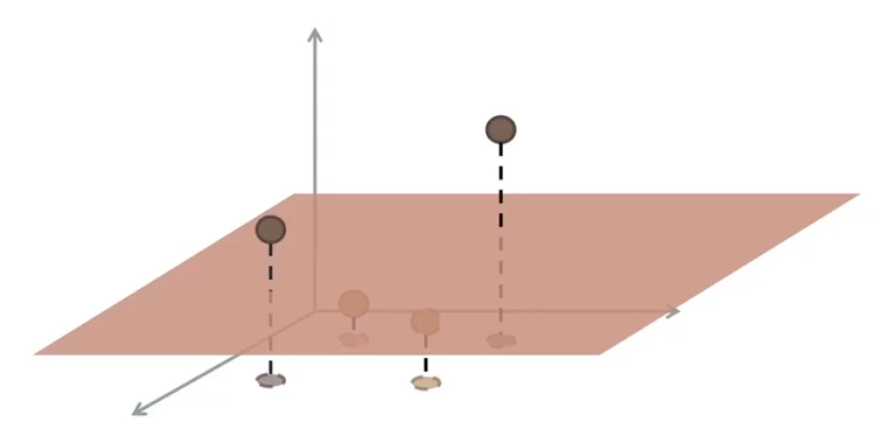
Nella trattazine dei metodi kernel sarà quindi necessario distinguere due tipologie di spazi:
Input space: Lo spazio iniziale dei dati del training set.
Feature space: Lo spazio mappato a partire dall'input space tramite la trasformazione (eventualmente non lineare) \(\Phi\).
Imponiamo una sola caratteristica allo spazio delle features: deve essere possibile definire un prodotto scalare su di esso. In altre parole, deve essere uno spazio di Hilbert.
Perché richiediamo l'esistenza del prodotto scalare nello spazio delle features?
Dalla trattazione delle SVMs avevamo visto che la classificazione finale di un nuovo punto \(\mathbf{x}\) poteva essere fatta in due modi diversi:
Utilizzando i parametri dell'iperpiano separatore \((\mathbf{w}, w_0)\).
Utilizzando i vari moltiplicatori di Lagrange \(\alpha_i\) trovati risolvendo il problema duale.
La seconda formulazione in particolare aveva la seguente forma
\[y(\mathbf{x}) = \sum\limits_{j \in \mathcal{S}} y_j \alpha_j \mathbf{x}_j \cdot \mathbf{x} + w_0\]
dove con \(\mathbf{x}_j \cdot \mathbf{x}\) stiamo intendendo il prodotto scalare tra i due vettori.
Supponiamo adesso di utilizzare una funzione \(\Phi\) per cambiare lo spazio su cui lavoriamo. Ogni punto è mappato da \(x\) a \(\Phi(x)\). La funzione di classificazione nel nuovo spazio può essere espressa nel seguente modo
\[y(\mathbf{x}) = \sum\limits_{j \in \mathcal{S}} y_j \alpha_j \Phi(\mathbf{x}_j) \cdot \Phi(\mathbf{x}) + w_0\]
dove \(\mathcal{S}\) è l'insieme degli indici associati ai vettori di supporto (a loro volta associati a moltiplicatori di lagrange non nulli).
Come possiamo vedere, la funzione non è cambiata molto: dobbiamo solo considerare il prodotto scalare tra l'immagine dei punti nel nuovo spazio piuttosto che con i punti originali.
Riflettiamo adesso su questo punto: per effettuare la classificazione nel nuovo spazio, dobbiamo solamente conoscere il prodotto scalare tra i vari punti in questo nuovo spazio.
Questa osservazione, che potrebbe non sembrare molto potente, in realtà lo è eccome. Il fatto che siamo solamente interessati al valore dei prodotti scalari infatti ci permette di lavorare anche con spazi che sarebbe difficile, se non del tutto impossibile, costruire in modo esplicito.
Per calcolare \(y(\mathbf{x})\) infatti abbiamo due strade:
La prima, la più intuitiva e immediata, è quella di conoscere in modo esplicito la costruzione del nuovo spazio tramite \(\Phi\), calcolare i vari \(\Phi(\mathbf{x}_j)\), e calcolare il prodotto scalare in modo esplicito.
La seconda, molto meno intuitiva, consiste invece nell'utilizzare una funzione particolare , che sarà chiamata funzione kernel, che associa ad ogni coppia di punti dello spazio originale il valore del prodotto scalare dei punti una volta che sono stati trasformati da \(\Phi\). In formula,
\[k(\mathbf{x}_i, \mathbf{x}_j) = \Phi(\mathbf{x}_i) \cdot \Phi(\mathbf{x}_j)\]
Il kernel trick consiste nell'utilizzare la funzione kernel per rappresentare implicitamente il nuovo spazio di lavoro ottenuto applicando la trasformazione \(\Phi\). Utilizzando la funzione kernel la classificazione è quindi calcolata come segue
\[y(\mathbf{x}) = \sum\limits_{j \in \mathcal{S}} y_j \alpha_j k(\mathbf{x}_j, \mathbf{x}) + w_0\]
La stessa cosa, ovvero sostituire \(\mathbf{x}_j \cdot\mathbf{x}\) con \(k(\mathbf{x}_j, \mathbf{x})\), può essere fatta anche durante il training per ottenere i moltiplicatori di lagrange ottimali \(\alpha_i\).
L'applicazione di questo kernel trick ci permette di fare cose molto interessanti: dato che rappresentiamo solo in modo implicito il nuovo spazio, diventa ad esempio possibile lavorare con spazi di dimensione infinita.
Andiamo adesso a caratterizzare meglio le funzioni kernel.
Non tutte le funzioni sono funzioni kernel.
Per quanto detto prima infatti una funzione kernel è una funzione che rappresenta in modo implicito una parte (i prodotti scalari) di un spazio ottenuto da una trasformazione (eventualmente non-lineare) \(\Phi\). Questo significa che ad ogni funzione kernel è associata una funzione base \(\Phi\).
Funzioni basi e funzioni kernel sono relazionate nel seguente modo:
La funzione base \(\Phi: \chi \to \mathcal{F}\) è una funzione che prende in input un punto \(x\) da uno spazio \(\chi\) (input space) e lo mappa in un'altro spazio \(\mathcal{F}\) (feature space) in cui deve essere possibile definire il prodotto scalare (ovvero deve essere uno spazio di Hilbert).
La funzione kernel \(\kappa: \chi \times \chi \to \mathbb{R}\) invece è una funzione che prende una coppia di punti dall'input space e ritorna il valore del loro prodotto scalare nello spazio delle features \(\mathcal{F}\)
\[\kappa(x_1, x_2) = \Phi(x_1) \cdot \Phi(x_2)\]
Notiamo poi che lo spazio di input non deve necessariamente essere un insieme numerico. Questo significa che possiamo considerare come input anche degli insiemi di stringhe, o di alberi, o di grafi, o di una qualsiasi altra cosa, e, utilizzando le funzioni kernel, possiamo direttamente affrontare problemi di classificazione senza andare prima a codificare le entità da classificare con dei vettori numerici.
Come facciamo a capire quando abbiamo tra le mani una funzione kernel?
La condizione necessaria e sufficiente più generale possibile che possiamo dare per rispondere a questa domanda è la seguente:
Mercer's theorem: Affinché una data funzione \(\kappa: \mathbb{R}^d \times \mathbb{R}^d \to \mathbb{R}\) sia una funzione kernel, dobbiamo avere che per tutti gli insiemi di \(n\) elementi \(\{x_1, \ldots, x_n\}\), la matrice di Gram \(\mathbf{G}\) definita come segue
\[G = \Big(\kappa(\mathbf{x}_i, \mathbf{x}_j) \Big)_{i, j = 1}^n\]
deve essere,
Simmetrica, ovvero
\[\kappa(\mathbf{x}_i, \mathbf{x}_j) = \kappa(\mathbf{x}_j, \mathbf{x}_i)\]
Semidefinita positiva, ovvero
\[v^T \mathbf{G} v \geq 0\]
per ogni vettore \(v\).
Anche se dal punto di vista teorico questa condizione caratterizza completamente le funzioni kernel, nella pratica è molto difficile da utilizzare. Esistono quindi metodi più costruttivi per ottenere una funzione kernel.
L'idea generale utilizzata nella pratica per lavorare con funzioni kernel è quella di partire da delle funzioni che già sappiamo essere funzioni kernel, combinarle tra loro e ottenere funzioni kernel sempre più complesse.
Per inizializzare questa procedura però abbiamo bisogno di dimostrare manualmente che alcune funzioni sono effettivamente funzioni kernel.
Consideriamo la seguente funzione e supponiamo che lo spazio di input è \(\mathbb{R}^2\).
\[\kappa(x, y) = (x \cdot y)^d\]
Possiamo dimostrare che per \(d = 2\) abbiamo una funzione kernel nel seguente modo
\[\begin{split} (x \cdot y)^2 &= \Big( (x_1, x_2) \cdot (y_1, y_2) \Big)^2 \\ &= \Big( x_1 y_1 + x_2 y_2 \Big)^2 \\ &= x_1^2 y_1^2 + x_2^2 y_2^2 + 2 x_1 y_1 x_2 y_2\\ &= \Big(x_1^2, \sqrt{2} x_1 x_2, x_2^2 \Big) \cdot \Big(y_1^2, \sqrt{2} y_1 y_2, y_2^2 \Big) \\ &= \Phi(x) \cdot \Phi(y) \\ \end{split}\]
dove \(\Phi\) è la funzione base associata a \(\kappa\) e definisce il seguente trasformazione
\[\Phi(x) := \Big( x_1^2, \sqrt{2} x_1 x_2, x_2^2 \Big)\]
In generale è possibile estendere il risultato trovato in precedenza sia al caso \(n\) dimensionale per \(d = 2\) e sia al caso \(n\) dimensionale e \(d\) intero positivo.
Siano \(\kappa_1()\) e \(\kappa_2()\) due funzioni kernel. Il risultato delle seguenti combinazioni dà sempre una funzione kernel.
\(e^{\kappa_1(x_1, x_2)}\)
\(\kappa_1(x_1, x_2) + \kappa_2(x_1, x_2)\)
\(\kappa_1(x_1, x_2) \kappa_2(x_1, x_2)\)
\(c \kappa_1(x_1, x_2)\) per ogni \(c > 0\)
\(x_1^T \mathbf{A} x_2\), con \(\mathbf{A}\) semi-definita positiva.
\(f(x_1) \kappa_1(x_1, x_2) g(x_2)\), per ogni \(f, g: \mathbb{R}^n \to \mathbb{R}\).
etc...
Supponiamo di voler dimostrare che la seguente funzione è una funzione kernel
\[\kappa(x_1, x_2) = (x_1 \cdot x_2 + c)^d\]
l'idea è quella di "costruirla" in piccoli steps:
Come prima cosa notiamo che \(x_1 \cdot x_2\) è la funzione kernel che corrisponde al caso in cui la funzione base è la funzione identità \(\Phi(x) = x\).
\(c\) invece è una funzione kernel, in quanto la relativa matrice di Gramm è semi-definita positiva e simmetrica.
Dai punti (1) e (2) segue che \(x_1 \cdot x_2 + c\) è una funzione kernel, in quanto la somma di due kernel è sempre un kernel.
Infine, elevare un kernel ad un coefficiente positivo \(d > 0\) ci dà sempre un kernel.
Per terminare la trattazione dei metodi kernel, andiamo a presentare sia i kernel più utilizzati quando partiamo già da uno spazio vettoriale, e sia due situazioni in cui definendo una opportuna funzione kernel siamo in grado di trattare problemi di classificazione anche senza definire una opportuna codifica vettoriale delle varie entità in gioco.
Tipicamente i kernel più utilizzati quando rappresentiamo lo spazio di input tramite vettori numerici sono i seguenti:
Polynomial kernel:
\[\kappa(x_1, x_2) = (x_1 \cdot x_2 + 1)^d\]
Sigmoidal kernel:
\[\kappa(x_1, x_2) = \tanh{(c_1 x_1 \cdot x_2 + c_2)}\]
Gaussian kernel:
\[\kappa(x_1, x_2) = \text{exp}\Big(- \frac{||x_1 - x_2||^2}{2 \sigma^2} \Big)\]
Fino adesso abbiamo trattato solamente di kernel che agiscono su spazi vettoriali e che quindi eseguono trasformazioni tra spazi continui in spazi continui. Detto questo, è anche possibile definire delle funzioni kernel che partono da insiemi di elementi discreti, e che tramite, procedure algoritmiche, mappano questi ultimi in spazi continui.
Consideriamo ad esempio la rappresentazione delle stringhe. Uno string kernel dovrebbe fornirci un metodo per mappare parole "simili" in vettori di numeri "simili". Un possibile approccio è quello di utilizzare le sottostringhe. In particolare, date due stringhe, più queste stringhe condividono sottostringhe uguali, e più sono "simili" nello spazio delle features su cui vengono mappate.
Uno string kernel deve quindi prendere in input due stringhe \(s\) e \(t\) e deve essere in grado di calcolare il numero reale \(k(s, t)\) tale che:
Esistono due vettori \(\overline{s}, \overline{t}\).
I vettori \(\overline{s}\) e \(\overline{t}\) sono unici fissati \(s\) e \(t\).
\(k(s, t) = \overline{s} \cdot \overline{t}\).
Per poter definire \(k(s, t)\) devo poter essere in grado di enumerare tutte le sottostringhe di lunghezza arbitraria. In altre parole sto mappando le mie stinghe nello spazio \(\mathbb{R}^{\infty}\), dove a ciascuna dimensione dello spazio di arrivo è associata una particolare sottostringa.