Neural Networks
Date:
Author: Leonardo Tamiano
Table of Contents:
Nel presente documento è riportata una piccola introduzione alle reti neurali.
Iniziamo con qualche note introduttia sul concetto di neurone, di rete neurale, e sul perché potremmo essere interessati alle reti neurali.
Nel contesto delle reti neurali la parola "neurone" viene utilizzata molto.
Ma che cos'è un neurone?
I neuroni in senso classico si trovano, sorprendentemente, nel nostro cervello. Graficamente sono rappresentati come segue
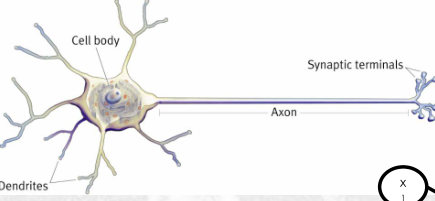
e in modo approssimato il loro funzionamento può essere descritto nel seguente modo:
Le cellule più importanti presenti nell'encefalo sono le cellule nervose, o neuroni, che sono circa dieci miliardi [...] Ciascun neurone possiede un certo numero di sinapsi poste sui dendriti e sul corpo cellulare. L'ingresso e l'uscita consistono di flussi elettrochimici, cioè di ioni in movimento. Tra le porte d'ingresso e il canale di uscita di un neurone sta il corpo cellulare, dove vengono prese le "decisioni".
Il tipo di decisione che deve prendere un neurone è questo: se debba o no scaricare, cioè se debba o no dare inizio a quel processo che provoca una particolare modificazione elettrochimica capace di propagarsi che è l'impulso nervoso. Se l'impulso parte, esso percorre tutto l'assone fino a raggiungere le porte d'ingresso di uno o più altri neuroni, facendo loro prendere lo stesso tipo di decisione.
La decisione viene presa in modo semplice: se la somma di tutti gli ingressi supera una certa soglia, allora si; altrimenti no. Certi ingressi possono essere negativi ed elidere ingressi positivi di altra provenienza.
Un neurone può avere qualcosa come 200.000 porte d'ingresso diverse. Lungo il percorso, l'assone può presentare una o parecchie biforcazioni.
Dopo aver scaricato, un neurone ha bisogno di una breve pausa (periodo refrattario) per recuperare la sua eccitabilità e poter scaricare di nuovo: di solito essa è dell'ordine del millisecondo, cosicché un neurone può scaricare circa fino a un migliaio di volte al secondo.
Douglas Hofstadter, Gödel, Escher, Bach.
Intorno alla metà del secolo scorso i matematici hanno preso spunto da questo funzionamento per definire il concetto di neurone dal punto di vista matematico.
Un "neurone matematico" è una unità computazionale formata da due parti:
Una prima parte, che calcola una combinazione lineare di determinati valori utilizzando dei particolari pesi. Vedremo successivamente che questi pesi saranno i parametri della rete neurale.
E una seconda parte che al risultato calcolato in precedenza applica una funzione eventualmente non lineare. Nel gergo delle reti neurali questa funzione non-lineare è chiamata funzione di attivazione.
Riassumendo quindi, troviamo la seguente equazione
\[\text{neuron} = \text{linear} + \text{activation}\]
Graficamente invece possiamo rappresentare un neurone matematico nel seguente modo
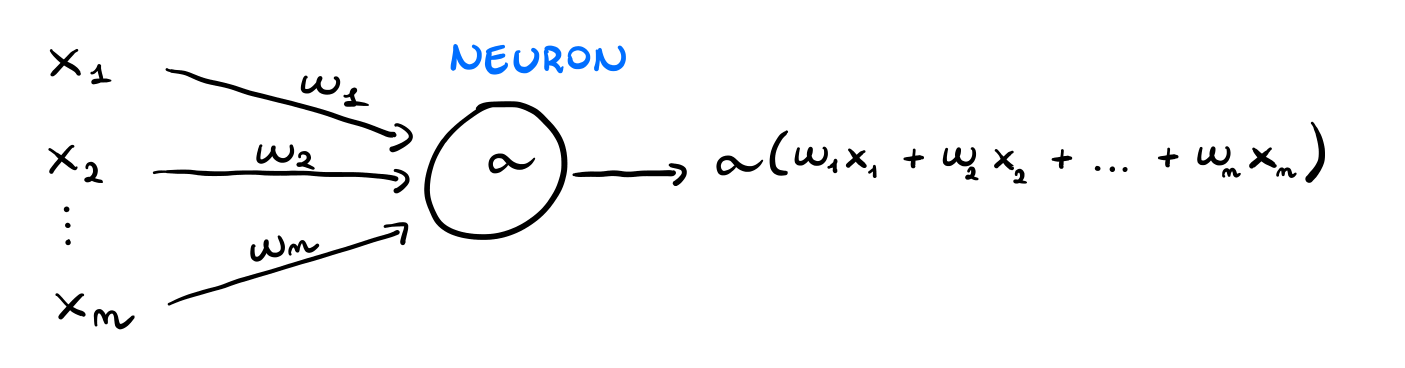
L'idea sottostante a tutti i metodi di apprendimento automatico che fanno utilizzo di reti neurali è quella di costruire dei modelli stratificati di neuroni andando a collegare l'output dei neuroni di uno strato con l'input dei neuroni dello strato successivo.
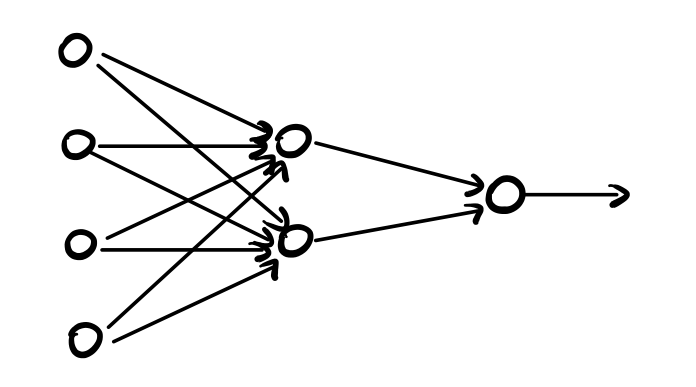
Un modello di rete neurale è quindi composto da due parti:
L'architettura: che specifica le connessioni tra i vari neuroni.
I parametri: che specificano i pesi delle varie connessioni tra i vari neuroni.
Una volta definita l'architettura di una rete neurale, per capire il valore ottimale dei parametri bisogna effettuare un processo di training. In un contesto supervisionato, la tecnica più semplice e più utilizzata per addestrare una rete neurale prende il nome di backpropagation.
Le reti neurali vengono principalmente utilizzare per il loro potere espressivo. È infatti possibile dimostrare che le reti neurali possono essere utilizzati come approssimatori universlai di funzione.
In particolare, data una funzione continua, è possibile costruire una rete neurale a tre livelli con funzioni di attivazione sigmoidali, in grado di approssimare con un grado di precisione arbitraria la funzione di interesse. Nella pratica però il livello di approssimabilità è legato al numero di nodi che si trovano nell'hidden layer.
Piuttosto che avere un numero sempre più grandi di nodi in ciascun layer, nel corso del tempo si sono sviluppate delle architetture, chiamate deep architectures, che aumentano il numero di layer stessi senza però sacrificare il potere espressivo.
Il primo esempio di approccio neurale (anche chiamato "connessionistico") è rappresentato dal perceptron (in italiano percettrone). Il percettrone è stato introdotto negli anni 60 ed è un modello semplice composto di un singolo "neurone".
Il percettrone ci permette di affrontare problemi di classificazione binaria in quanto calcola un iperpiano di separazione, e classifica i punti a seconda di come questi vengono divisi dall'iperpiano calcolato. Questo vuol dire che in termine di output, il percettrone è molto simile all'approccio SVM trattato in precedenza.
Da un punto di vista algebrico il percettrone può essere descritto come segue: dato un elemento \(\mathbf{x}\) da classificare, il percettrone calcola la seguente funzione
\[h(\mathbf{x}) = \text{sign} \Big(\sum\limits_{i = 1}^n w_i x_i + b \Big)\]
dove,
\(\text{sign}\) è la funzione segno, definita come segue
\[\text{sign}(x) = \begin{cases} 1 &, x \geq 0 \\ -1 &, x < 0 \\ \end{cases}\]
\(b\) è il bias.
\(\mathbf{w} = (w_1, \ldots, w_n)\) è un vettore che contiene i pesi applicati ai diversi valori delle features di \(\mathbf{x}\).
Come possiamo vedere quindi il percettrone è un modello lineare generalizzato in quanto alla combinazione lineare delle features è applicata una funzione eventualmente non lineare (la funzione segno).
Graficamente possiamo rappresentare il percettrone come segue
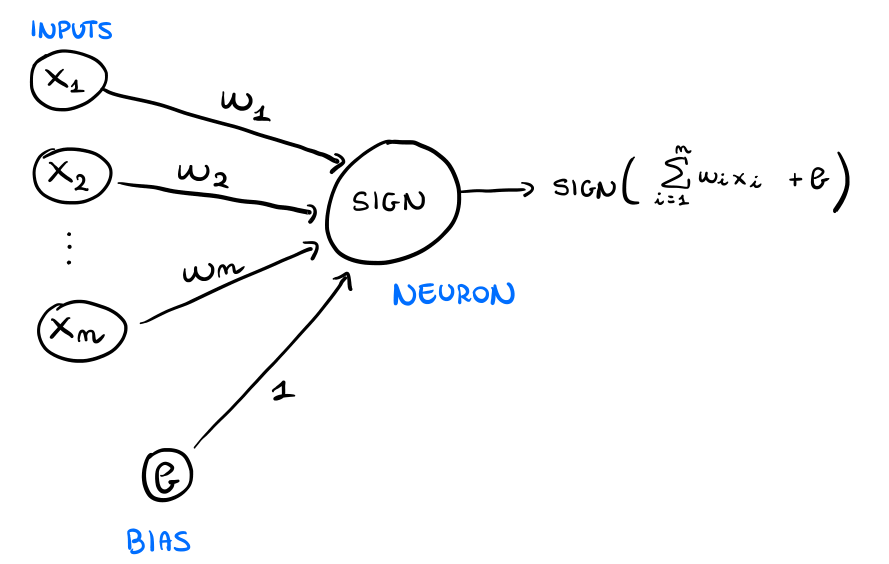
Dato un training set \(D\) in cui ad ogni esempio da classificare \(\mathbf{x}_i\) è associato il label di una classe \(y_i \in \{1, -1\}\), dove se \(y_i = 1\) allora \(x_i \in C_1\) mentre se \(y_i = -1\) allora \(x_i \in C_2\), addestrare un percettrone significa trovare i valori dei parametri \(w_i\) e \(b\) a partire dal training set \(D\).
Per trovare questi valori l'idea è quella di definire una funzione di costo e di ricercare nello spazio dei parametri il valore dei parametri che minimizzano tale funzione.
A questo punto ci chiediamo: che funzione di costo possiamo utilizzare? Consideriamo qualche alternativa:
Se ad esempio calcoliamo il numero di elementi del training set classificati male, otterremo sì una funzione di costo, ma una funzione piecewise constant. Questo tipo di funzione non ci permetterebbe di utilizzare tecniche di ottimizzazione come la discesa del gradiente, e dunque è da evitare.
Un'altra funzione di costo potrebbe essere definita nel seguente modo: ogni elemento del training set classificato bene non influisce sulla funzione di costo, mentre se \(x_i\) è un elemento classificato male, allora il suo contributo al costo totale è dato da
\[- \Big( \sum\limits_{i = 1}^n w_i x_i + b \Big) \cdot y_i\]
notiamo infatti che se \(x_i\) è classificato male allora tale valore è sempre positivo. La funzione costo finale è quindi data da
\[E_p(\mathbf{w}, b) = -\sum\limits_{\mathbf{x}_i \in \mathcal{M}}\Big(\sum\limits_{j = 1}^n w_j x_{ij} + b \Big) y_i\]
A partire da questa seconda funzione di costo, che è differenziabile, possiamo applicare la tecnica nota con il nome di discesa del gradiente stocastica.
Per utilizzare questa tecnica dobbiamo prima calcolare il gradiente della funzione costo rispetto ai vari parametri.
\[\begin{split} \Delta_{\mathbf{w}} E_p(\mathbf{w}, b) &= - \sum\limits_{x_i \in \mathcal{M}} y_i \cdot x_i \\ \\ \frac{\partial }{\partial b} E_p(\mathbf{w}, b) &= - \sum\limits_{x_i \in \mathcal{M}} y_i \\ \end{split}\]
L'algoritmo della discesa del gradiente stocastica consiste quindi nell'inizializzare i parametri in modo randomico e nell'aggiornare i vari parametri ogni volta che incontriamo un esempio classificato male.
Initialize w, b
k := 0
while (not all_elements_are_well_classified):
k = k + 1
i = (k mod n) + 1
// found wrongly classified element
if sign(w * x_i + b) * y_i:
// update parameters
w = w + eta * x_i * y_i
b = b + eta * y_i
dove eta \((\eta)\) rappresenta la learning rate.
A differenza della classica discesa del gradiente, nella discesa del gradiente stocastica si considera il gradiente rispetto ad un solo elemento del training set.
Il percettrone ha alcuni limiti da tenere a mente, tra cui troviamo i seguenti:
È difficile valutare l'output di un percettrone in termini di probabilità.
Funziona solamente quando le classi sono linearmente separabili.
Permette di calcolare solamente linear decision boundaries.
Mentre la prima condizione non è poi così grave, in quanto vale anche per altri modelli già visti, la seconda condizione invece è molto più forte. Molte volte infatti i dati con cui lavoriamo sono sporchi, o comunque non sono linearmente separabili.
Il grosso problema segue dal fatto che, nel caso in cui le classi sono linearmente separabili, l'algoritmo del percettrone fatto vedere prima converge ad un separatore lineare, ma se invece le classi non sono linearmente separabili, allora l'algoritmo non converge ma continua a ciclare in un insieme di possibili soluzioni.
A rendere la seconda condizione ancora più grave è poi il fatto che non è possibile valutare a priori se i dati con cui lavoriamo sono linearmente separabili oppure no.
Per quanto riguarda il terzo limite invece, osserviamo come il percettrone non è in grado di rappresentare l'operazione logica XOR. Consideriamo infatti il problema di rappresentare il risultato dell'operatore XOR tra due bit
\[\begin{array}{c | c | c} \textbf{Input 1} & \textbf{Input 2} & \textbf{XOR} \\ \hline 0 & 0 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \\ 1 & 1 & 0 \\ \end{array}\]
Osserviamo che per come è definita la funzione, non è possibile spezzare i quattro punti in modo lineare.
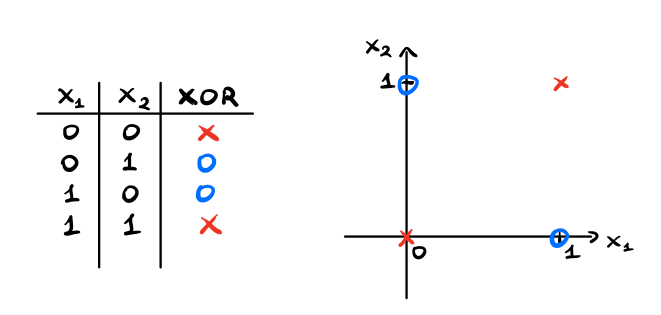
Questo significa che esistono funzioni, come la funzione XOR, che non possono essere calcolate utilizzando un singolo percettrone.
Per cercare di superare i limiti di rappresentazione dei singoli percettroni si è quindi pensato di connettere vari neuroni tra loro al fine di formare reti neurali più complesse, e, si spera, anche più potenti.
Un primo esempio di rete neurale stratificata prende il nome di multilayer perceptron, ed è ottenuta combinando tra loro singole unità neuronali simili a percettroni (ma che possono utilizzare anche funzioni di attivazioni diverse dal percettrone).
Consideriamo ad esempio il problema di calcolare la funzione XOR. Come avevamo già visto, con un singolo percettrone non siamo in grado di effettuare questo calcolo. Consideriamo però la seguente rete
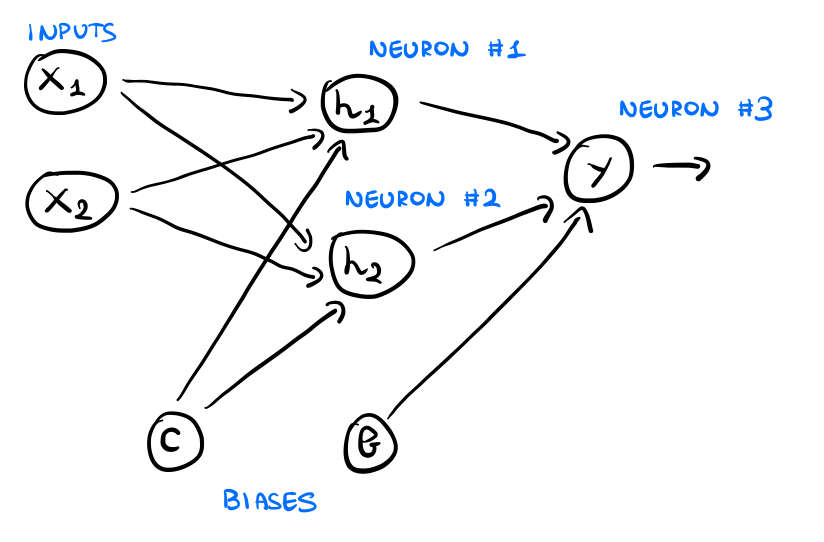
Come possiamo vedere, questa nuova rete è divisa in strati e contiene ben \(3\) neuroni. I vari strati di interesse della rete sono i seguenti
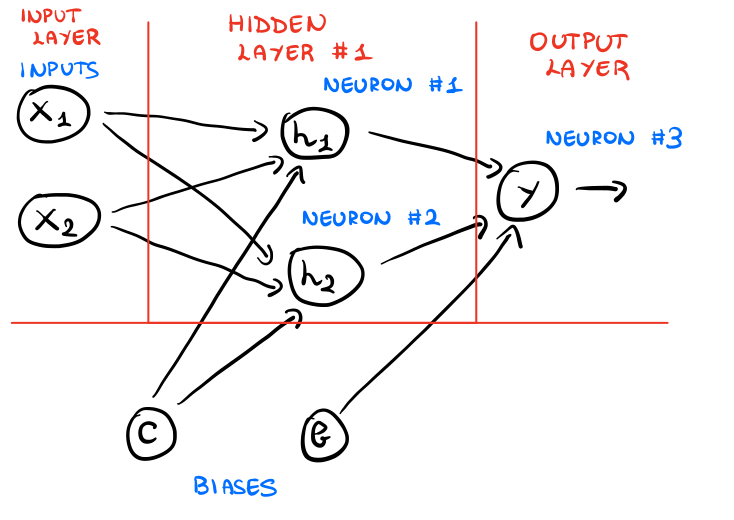
che descritti brevemente sono:
Input Layer: Questo layer contiene i valori delle varie componenti dell'input. Nel nostro caso le componenti sono due variabili booleane \(x_1, x_2\), ciascuna delle quali può assumere un valore in \(\{0, 1\}\).
Hidden Layer n.1: Questo layer contiene i primi due neuroni. Ciascun neurone di questo layer combina i valori delle componenti dell'input tramite dei pesi, aggiunge al risultato il bias \(c\), e successivamente applica una funzione di attivazione. Questo layer è chiamato "hidden" in quanto si trova tra l'input (visibile dall'esterno), e l'output (sempre visibile dall'esterno).
Output layer: Questo layer contiene un solo neurone, che alla fine, idealmente, dovrebbe ritornare il valore della funzione XOR applicata ai valori di input.
Per far in modo che la nostra rete calcoli proprio la funzione XOR andiamo poi ad effettuare le seguenti scelte:
Per il primo (e unico) hidden layer, tutti i neuroni hanno come funzione di attivazione la funzione \(\text{max}(x) := \max \{0, x\}\).
L'output layer invece ha come funzione di attivazione la funzione identità \(\text{id}(x) := x\).
Infine, i pesi della rete sono specificati come segue
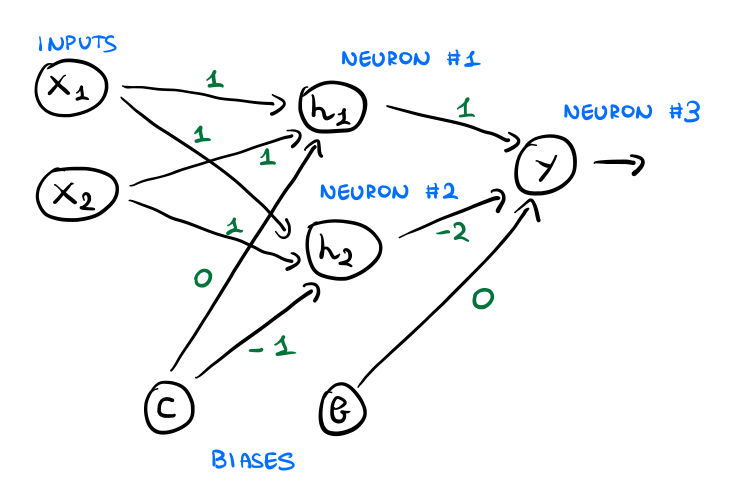
Osserviamo a questo punto che un modo più coinciso per specificare i pesi dei vari neuroni nei vari layers è tramite il linguaggio delle matrici. In particolare troviamo che
Le connessioni tra l'input layer e il primo hidden layer sono descritte nel seguente modo
\[\mathbf{W} = \begin{bmatrix} 1 & 1 \\ 1 & 1 \\ \end{bmatrix} \;\;\;,\;\;\; \mathbf{c} = \begin{bmatrix} 0 \\ -1 \\ \end{bmatrix}\]
dove in particolare le righe della matrice \(\mathbf{W}\) descrivono i pesi che connettono ciascun neurone ai valori delle componenti dell'input, mentre il vettore colonna \(\mathbf{c}\) descrive quali sono i bias due due neuroni (considerando \(c=b=1\) il peso dell'arco determina il valore del bias per il particolare neurone del layer).
Le connessioni tra il primo hidden layer e l'output layer invece sono descritte nel seguente modo
\[\mathbf{w} = \begin{bmatrix} 1 \\ -2 \\ \end{bmatrix} \;\;\;,\;\;\; b = 0\]
Una volta che abbiamo definito sia l'architettura che i parametri della nostra rete, possiamo vedere che essa è in grado di calcolare la funzione XOR come segue:
Se \(x_1 = x_2 = 0\), allora per calcolare l'output della rete procediamo nel seguente modo
Valore calcolato dal neurone \(h_1\):
\[\begin{split} \max\{0, x_1 \cdot 1 + x_2 \cdot 1 + 0 \} &= \max\{0, 0 \cdot 1 + 0 \cdot 1 + 0 \} \\ &= \max\{0, 0\} \\ &= 0 \end{split}\]
Valore calcolato dal neurone \(h_2\):
\[\begin{split} \max\{0, x_1 \cdot 1 + x_2 \cdot 1 - 1 \} &= \max\{0, 0 \cdot 1 + 0 \cdot 1 - 1 \} \\ &= \max\{0, -1\} \\ &= 0 \end{split}\]
Valore calcolato dal neurone \(y\):
\[\text{id}(0 \cdot 1 + 0 \cdot (-2) + 0) = \text{id}(0) = 0\]
Dunque in questo caso la rete ritorna \(0\).
Se \(x_1 = 1\) e \(x_2 = 0\), allora
Valore calcolato dal neurone \(h_1\):
\[\begin{split} \max\{0, x_1 \cdot 1 + x_2 \cdot 1 + 0 \} &= \max\{0, 1 \cdot 1 + 0 \cdot 1 + 0 \} \\ &= \max\{0, 1\} \\ &= 1 \end{split}\]
Valore calcolato dal neurone \(h_2\):
\[\begin{split} \max\{0, x_1 \cdot 1 + x_2 \cdot 1 - 1\} &= \max\{0, 1 \cdot 1 + 0 \cdot 1 - 1 \} \\ &= \max\{0, 0\} \\ &= 0 \end{split}\]
Valore calcolato dal neurone \(y\):
\[\text{id}(1 \cdot 1 + 0 \cdot (-2) + 0) = \text{id}(1) = 1\]
Dunque in questo caso la rete ritorna \(1\).
Andando a vedere i restanti casi è possibile dimostrare che questa rete riesce a calcolare la funzione XOR.
Cerchiamo adesso di generalizzare quanto visto prima andando a descrivere in generale come possiamo specificare una feedforward neural network, ovvero una rete neurale in cui le connessioni tra i nodi della rete non formano cicli.
Data una rete neurale, troviamo i seguenti elementi di interesse:
\(n_l\), che rappresenta il numero di layers della rete.
\(s_l\), il numero di unità dell'input layer (ovvero la dimensione dell'input).
Il layer \(l\) e il layer \(l+1\) sono connessi tramite una matrice \(\mathbf{W}^{(l)}\) di parametri, in cui il parametro \(w^{(l)}_{i, j}\) connette l' \(i\) esimo neurone del layer successivo al \(j\) esimo neurone del layer precedente.
\(b_i^{(l)}\) è il bias associato al neurone \(i\) nel layer \(l+1\).
Andiamo adesso a descrivere in dettaglio i vari layers.
A seconda del particolare input che la nostra rete neurale deve leggere, l'input layer avrà un determinato numero di nodi.
Ad esempio, se l'input è formato da \(n\) elementi, \(x = (x_1, \ldots, x_n)\), allora l'input layer sarà formato da \(n\) nodi.
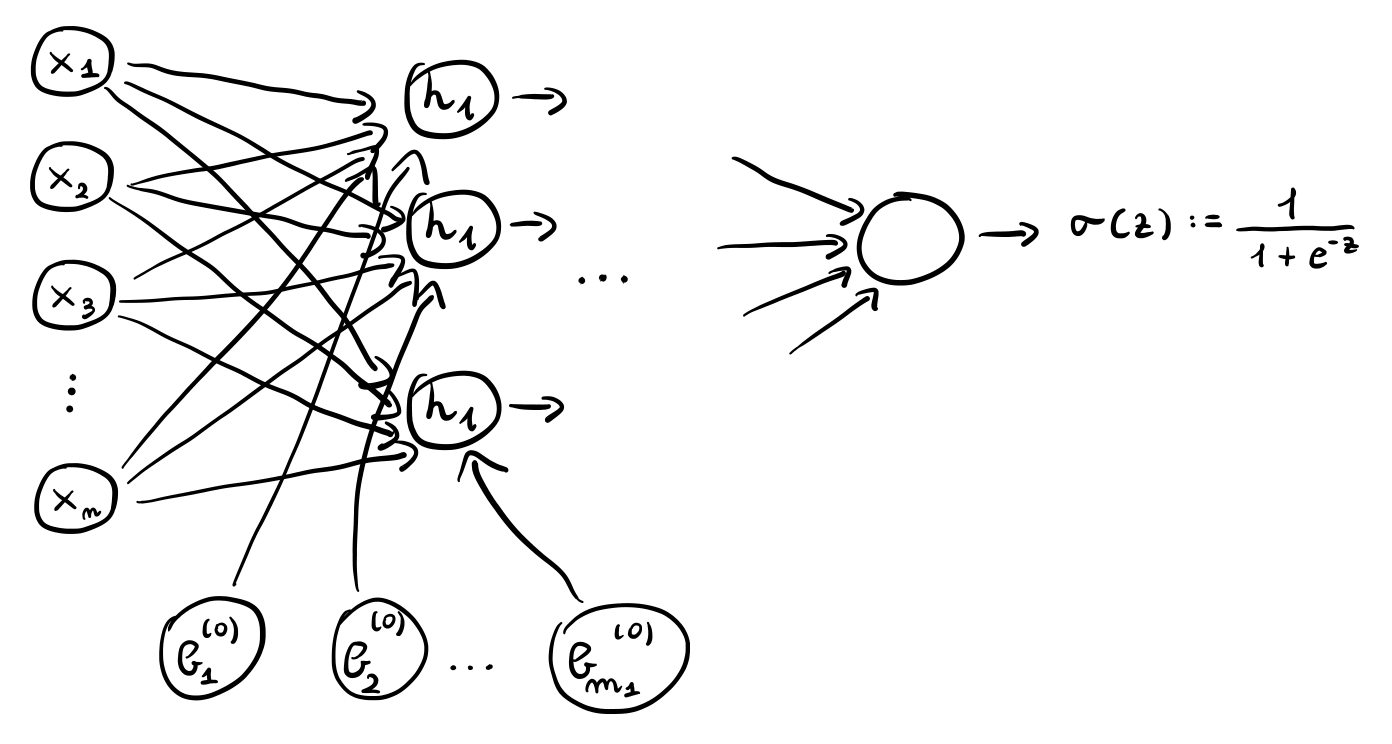
Il primo hidden layer è caratterizzato da \(m_1\) valori \(z_1^{(1)}, z_2^{(1)}, \ldots, z_{m_1}^{(1)}\), ciascuno dei quali è ottenuto combinando gli elementi dell'input tramite i pesi specificati dalla matrice \(\mathbf{W}^{(0)}\).
\[z_j^{(1)} = \sum\limits_{i = 1}^n w_{j,i}^{(0)} x_i + b_j^{(0)}\]
Detto in altre parole, \(z_j^{(1)}\) è ottenuto prendendo la \(j\) esima riga della matrice \(\mathbf{W}^{(0)}\), moltiplicandola termine per termine con il vettore di input \(x\) e sommando il bias \(b_j^{(0)}\).
Ogni valore \(z_j^{(1)}\) viene poi trasformato tramite una funzione di attivazione \(h_1\) per ottenere il valore \(a_j^{(1)}\).
\[a_j^{(1)} = h_1(z_j^{(1)})\]
Alla fine quindi l'output del primo hidden layer è il vettore
\[\mathbf{a}^{(1)} = (a_1^{(1)}, a_2^{(1)}, \ldots, a_{m_1}^{(1)})\]
Graficamente,
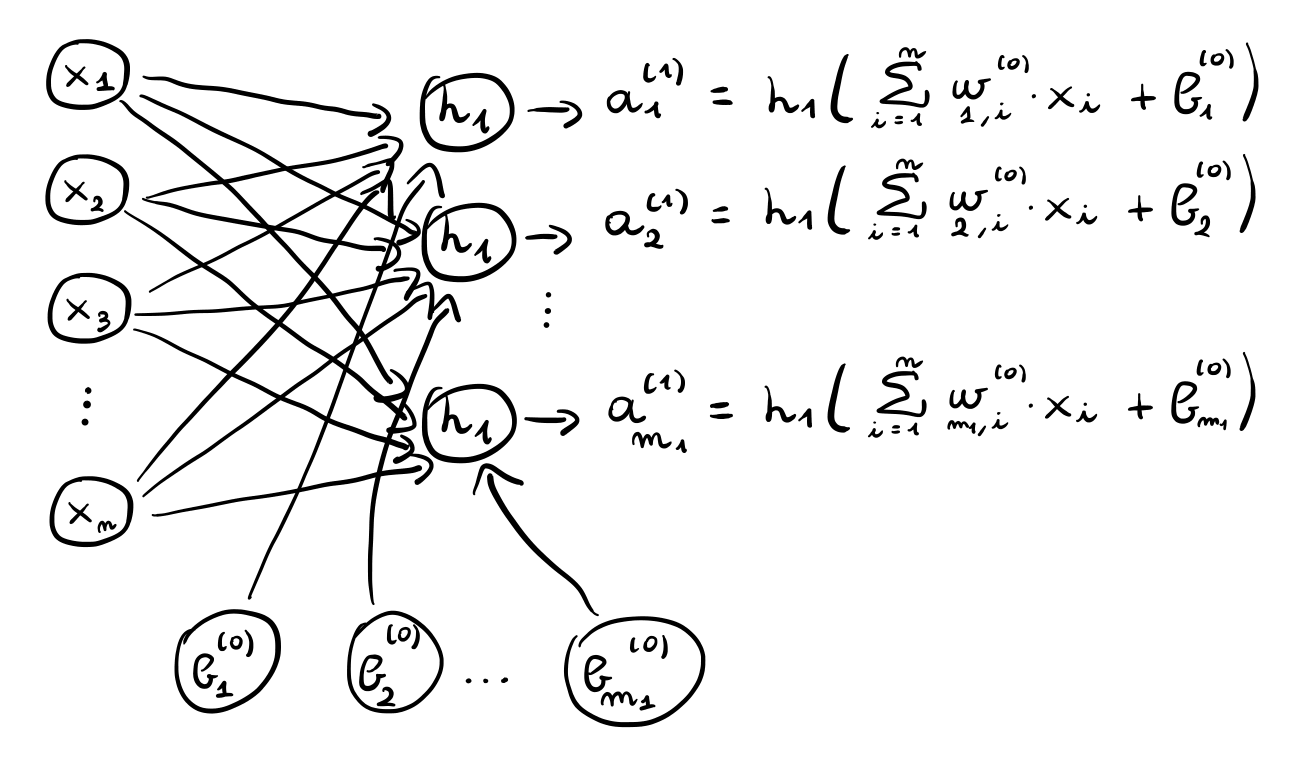
Come è possibile vedere quindi, il totale dei coefficienti relativi al primo layer è \((n + 1) \cdot m_1\), dove \(m_1\) è un iperparametro del modello che specifica il numero di neuroni del primo hidden layer.
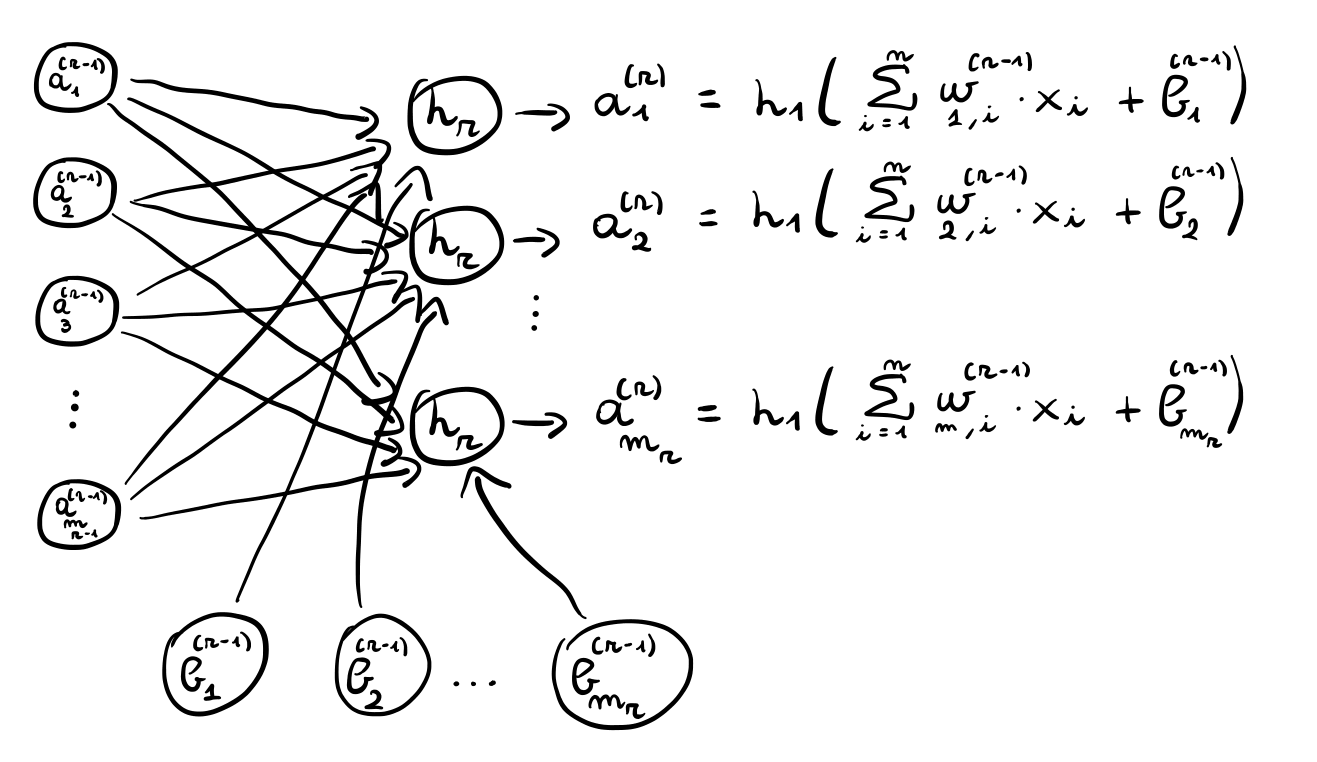
La stessa costruzione di prima può essere iterata per ogni layer interno. In particolare consideriamo il layer \(r\) con \(m_r\) unità. Questo layer utilizza come input il vettore generato dal layer precedente, ovvero \(\mathbf{a}^{(r-1)}\), per generare a sua volta il vettore di valori \(\mathbf{a}^{(r)}\) che passerà al successivo layer.
Il vettore \(\mathbf{a}^{(r)}\) è ottenuto applicando la funzione di attivazione non lineare \(h_r\) ad ogni \(z_j^{(r)}\) per \(j = 1, \ldots, m_r\), dove
\[z_j^{(r)} = \sum\limits_{i = 1}^{m_{r-1}} w_{j, i}^{(r-1)} \cdot a_i^{(r-1)} + b_j^{(r-1)}\]
Graficamente,
Alla fine di tutti gli hidden layers troviamo il layout di output.
Il layer di output è caratterizzato dal fatto che i valori in uscita da questo layer devono poter essere interpretati in funzione del problema che stiamo tentando di risolvere attraverso la rete neturale.
Possibili strutture a seconda del problema da affrontare per questo layer sono:
Regressione: In questo caso l'ultimo layer ci deve fornire un valore, e quindi l'output ritornato è un solo valore.
Classificazione binaria: Anche in questo caso l'output ritornato è un solo valore.
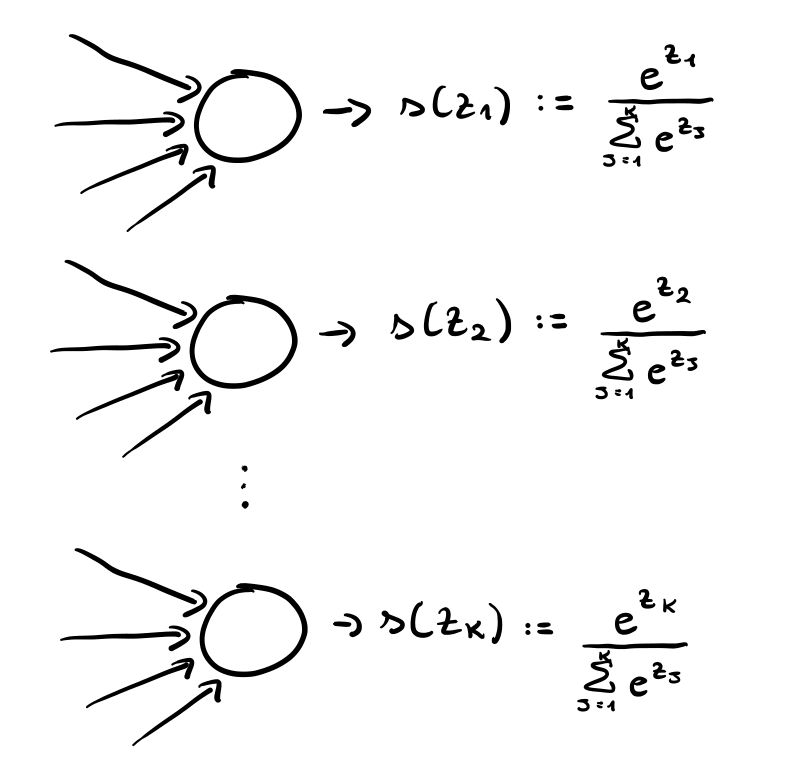
Classificazione multiclasse: A differenza dei precedenti, in questo caso, l'output layer dovrà ritornare \(k\) valori diversi, dove \(k\) è il numeri di classi diverse del nostro problema. Ciascun valore rappresenterà la probabilità di appartenere ad una particolare classe, e dunque in questo caso dobbiamo imporre che la somma di tali valori sia \(1\).
In generale quindi il layer \(n_l\), quello di output, fornisce un vettore di output
\[\mathbf{y} = \mathbf{a}^{(n_l)}\]
prodotto nuovamente da \(m_{n_l}\) neuroni (output units) che prima calcolano una combinazione lineare
\[z_j^{(n_l)} = \sum\limits_{i = 1}^{m_{n_l - 1}} w_{j, i}^{(n_l - 1)} \cdot z_i^{(n_l - 1)} + b_j^{(n_l - 1)}\]
e poi applicano una funzione di attivazione non lineare \(h_{n_l}\).
\[a_j^{(n_l)} = h_{n_l}(z_j^{(n_l)})\]
Per l'output layer la funzione di attivazione utilizzata dipende dal particolare problema affrontato. In particolare troviamo:
Regressione: \(h_{n_l}\) è la funzione identità.
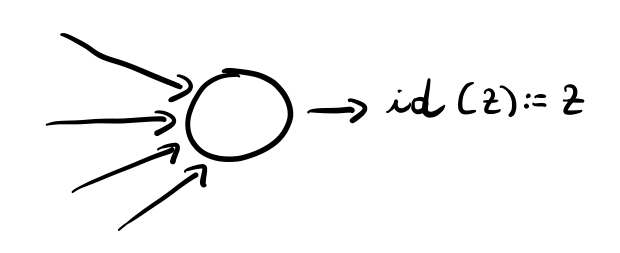
Classificazione (binaria): \(h_{n_l}\) è la funzione sigmoide.
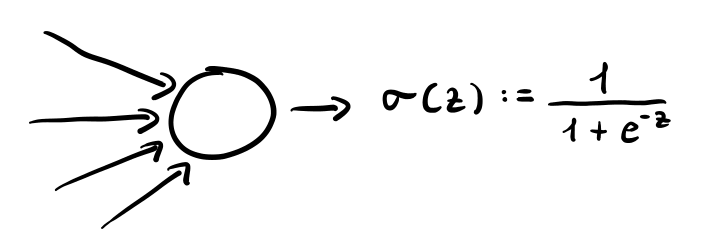
Classificazione (multiclasse): \(h_{n_l}\) è la funzione softmax.
Mettendo tutto assieme troviamo quindi la seguente struttura
Notiamo che il potere espressivo delle reti neurali deriva proprio dal fatto che ogni neurone applica una funzione di attivazione non-lineare alla combinazione lineare calcolata.
La scelta di quali funzioni di attivazione utilizzare è una scelta di design che determina l'architettura della nostra rete neurale. In generale ogni neurone può avere una funzione di attivazione diversa, ma in pratica molto spesso si utilizza la stessa funzione di attivazione per tutti i neuroni dello stesso strato.
Tra tutte le funzioni di attivazione che possiamo utilizzare troviamo le seguenti:
id
\[id(z) := z\]
tanh
\[\text{tanh}(z) := \frac{e^z - e^{-z}}{e^z + e^{-z}}\]
sigmoid
\[\sigma(z) := \frac{1}{1 + e^{-z}}\]
ReLU
\[\text{ReLU}(z) := \begin{cases} z &,\;\; z > 0 \\ 0 &,\;\; z \leq 0 \\ \end{cases}\]
Graficamente,
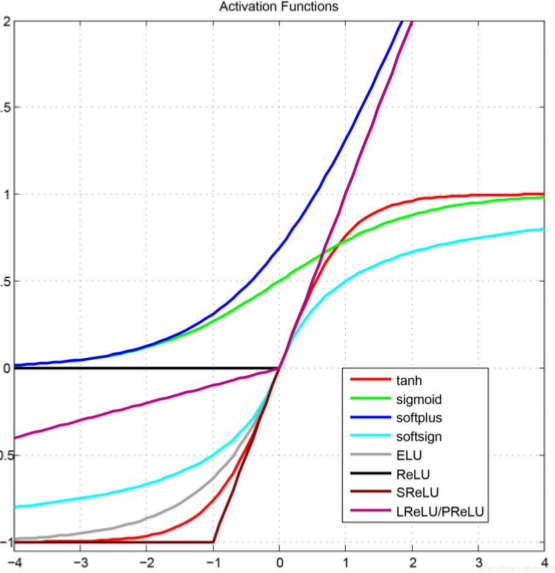
In generale una funzione di attivazione deve essere facilmente differenziabile.
Supponiamo di aver addestrato il modello, o anche di aver inizializzato i pesi del nostro modello a dei valori randomici. L'algoritmo feedforward viene utilizzato per calcolare l'output della rete dato l'input \(x\).
L'algoritmo consiste nell'effettuare un prodotto matriciale per ogni strato della rete.
Per velocizzare l'applicazione del modello a più elementi è poi possibile vettorizzare le operazioni.
Per quanto riguarda invece il training del modello, l'idea è quella di utilizzare il backpropagation algorithm.
Questo algoritmo si basa sulla discesa del gradiente, ovvero ricerca nello spazio dei parametri della rete il valore dei parametri che minimizza una fissata funzione di costo.
L'algoritmo è chiamato "backpropagation algorithm" in quanto può essere interpretato come una propagazione al contrario (backward propagation) di una computazione nella rete, che parte dall'output layer e và verso le unità di inputs. L'algoritmo in particolare calcola, per ogni strato, il contributo che ciascun parametro ha rispetto all'errore totale.
Per poter applicare il backpropagation algorithm dobbiamo quindi calcolare il gradiente della funzione di costo rispetto al vettore dei parametri. L'idea chiave però è quella di calcolare questo gradiente in modo intelligente tramite l'applicazione della chain rule, osservando il fatto che l'output della rete è una funzione composta tremendamente complessa ottenuta a partire da funzioni leggermente più semplici.
Consideriamo una rete neurale per un problema di classificazione binaria in cui la funzione di attivazione dell'output layer è la funzione sigmoide.
Definiamo la loss \(J\) rispetto al training set come la seguente somma
\[J = \sum\limits_{i = 1}^n \mathcal{L}_i\]
dove \(\mathcal{L}_i\) è la loss relativa all' \(i\) esimo elemento del training set \(D = \{(x_1, y_1), \ldots, (x_n, y_n)\}\) ed è definita come segue (cross-entropy):
\[\mathcal{L}_i = - \Big( y_i \cdot \ln \hat{y}_i + (1 - y_i) \cdot \ln{(1 - \hat{y}_i)} \Big)\]
dove \(\hat{y}_i\) è il risultato ottenuto utilizzando la rete neurale con input \(x_i\).
Notiamo che dalla linearità della derivata, riuscendo a calcolare la derivata parziale di \(\mathcal{L}_i\) rispetto ad ogni parametro della rete, siamo anche in grado di calcolare la derivata dell'intera funzione di costo rispetto ad ogni parametro dalla rete, in quanto
\[\frac{\partial J}{\partial w_{i,j}^{(k)}} = \sum\limits_{i = 1}^n \frac{\partial \mathcal{L}_i}{\partial w_{i,j}^{(k)}}\]
Possiamo quindi concentrarci sul calcolare \(\frac{\partial \mathcal{L}_i}{\partial w_{i,j}^{(l)}}\) rispetto ad un singolo elemento del training set \((x_i, y_i)\). Per eseguire questo calcolo consideriamo la seguente situazione
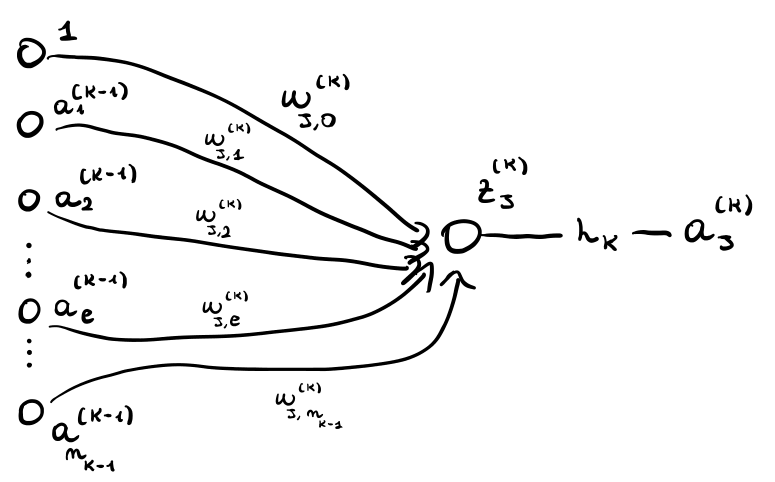
dove algebricamente abbiamo
\[a_j^{(k)} = h_k(z_j^{(k)}) = h_k\Bigg(\sum\limits_{r = 1}^{n_{k-1}} w_{j,r}^{(k)} \cdot a_r^{(k-1)}\Bigg)\]
L'idea sarà quella di utilizzare la chain rule nel seguente modo
\[\frac{\partial \mathcal{L}_i}{\partial w_{j,l}^{(k)}} = \frac{\partial \mathcal{L}_i}{\partial a_j^{(k)}} \cdot \frac{\partial a_j^{(k)}}{\partial z_j^{(k)}} \cdot \frac{\partial z_j^{(k)}}{\partial w_{j,l}^{(k)}}\]
dove i primi due termini formano quello che viene chiamato error term, identificato con \(\delta_j^{(k)}\) e definito come segue
\[\delta_j^{(k)} := \frac{\partial \mathcal{L}_i}{\partial z_j^{(k)}} = \frac{\partial \mathcal{L}_i}{\partial a_j^{(k)}} \cdot \frac{\partial a_j^{(k)}}{\partial z_j^{(k)}}\]
Iniziamo quindi osservando che, a prescindere dal layer in cui ci troviamo, abbiamo sempre che
\[\frac{\partial z_j^{(k)}}{\partial w_{j,l}^{(k)}} = \frac{\partial }{\partial w_{j, l}^{(k)}} \Big[ \sum\limits_{r = 1}^{n_{k-1}} w_{j,r}^{(k)} \cdot a_r^{(k-1)} \Big] = a_l^{(k-1)}\]
\[\frac{\partial a_j^{(k)}}{\partial z_j^{(k)}} = \frac{\partial}{\partial z_j^{(k)}} \Big[ h_k(z_j^{(k)}) \Big] = h^{'}_k(z_j^{(k)})\]
Questo significa che il contributo del generico parametro \(w_{j,l}^{(k)}\) alla loss \(\mathcal{L}_i\), è ottenuto moltiplicando l'error term \(\delta_j^{(k)}\) per il valore \(a_l^{(k-1)}\)
\[\frac{\partial \mathcal{L}_i}{\partial w_{i,j}^{(k)}} = \frac{\partial \mathcal{L}_i}{\partial a_j^{(k)}} \cdot \frac{\partial a_j^{(k)}}{\partial z_j^{(k)}} \cdot \frac{\partial z_j^{(k)}}{\partial w_{j,l}^{(k)}} = \delta_j^{(k)} \cdot a_l^{(k-1)}\]
Per quanto riguarda l'error term \(\delta_j^{(k)}\) invece, consideriamo due casi:
Quando il \(k\) esimo layer è l'ultimo layer della rete neurale.
Quando il \(k\) esimo layer è un hidden layer.
Se \(k\) esimo layer è l'ultimo layer allora la funzione di attivazione \(h_k\) è una funzione sigmoide
\[h_k(z) = \sigma(z) := \frac{1}{1 + e^{-z}}\]
Ricordiamo (ci tornerà utile a breve), che una proprietà importante della sigmoide è la seguente
\[\sigma^{'}(z) = \sigma(z)(1 - \sigma(z))\]
Possiamo quindi procedere con il calcolo dell'error term: per quanto riguarda il secondo termine abbiamo
\[\begin{split} \frac{\partial a_j^{(k)}}{\partial z_j^{(k)}} &= \frac{\partial}{\partial z_j^{(k)}} \Big[ h_k(z_j^{(k)}) \Big] \\ &= h^{'}_k(z_j^{(k)}) \\ &= h(z_j^{(k)}) \cdot (1 - h(z_j^{(k)})) \\ &= a_j^{(k)} \cdot (1 - a_j^{(k)}) \\ \end{split}\]
mentre per il primo termine, notando che \(\hat{y}_i = a_j^{(k)}\) in quanto \(k\) è l'ultimo layer, troviamo
\[\begin{split} \frac{\partial \mathcal{L}_i}{\partial a_j^{(k)}} &= \frac{\partial}{\partial a_j^{(k)}} -\Big[y_i \ln{a_j^{(k)}} + (1 - y_i) \cdot \ln{(1 - a_j^{(k)})} \Big] \\ &= - \frac{\partial}{\partial a_j^{(k)}} \Big[ y_i \ln{a_j^{(k)}} \Big] -\frac{\partial}{\partial a_j^{(k)}} \Big[ (1 - y_i) \ln{(1 - a_j^{(k)})} \Big] \\ &= - y_i \cdot \frac{\partial \ln{a_j^{(k)}}}{\partial a_j^{(k)}} - (1 - y_i) \cdot \frac{\partial \ln{(1 - a_j^{(k)})}}{\partial a_j^{(k)}} \\ &= y_i \cdot \frac{1}{a_j^{(k)}} - (1 - y_i) \cdot \frac{1}{1 - a_j^{(k)}} \cdot (-1) \\ &= \;\; ... \\ &= \frac{a_j^{(k)} - y_i}{a_j^{(k)}(1 - a_j^{(k)})} \\ \end{split}\]
Mettendo questi due termini assieme troviamo la seguente espressione per l'error term relativo alle unità dell'output layer (che in realtà è solo una)
\[\begin{split} \delta_j^{(k)} &= \frac{\partial \mathcal{L}_i}{\partial a_j^{(k)}} \cdot \frac{\partial a_j^{(k)}}{\partial z_j^{(k)}} \\ &= \frac{a_j^{(k)} - y_i}{a_j^{(k)}(1 - a_j^{(k)})} \cdot a_j^{(k)} (1 - a_j^{(k)}) \\ &= a_j^{(k)} - y_i \\ \end{split}\]
e quindi il contributo del generico paramatro \(w_{j, l}^{(k)}\) che finisce nell'output layer è dato da
\[\frac{\partial \mathcal{L}_i}{\partial w_{j, l}^{(k)}} = \Big( a_j^{(k)} - y_i) \Big) \cdot a_l^{(k-1)}\]
Se invece il \(k\) esimo layer è un hidden layer, allora possiamo calcolare l'error term come segue
\[\begin{split} \delta_j^{(k)} &= \frac{\partial \mathcal{L}_i}{\partial z_j^{(k)}} \\ &= \sum\limits_{r = 1}^{n_{k + 1}} \frac{\partial \mathcal{L}_i}{\partial z_r^{(k+1)}} \cdot \frac{\partial z_r^{(k+1)}}{\partial z_j^{(k)}} \\ &= \sum\limits_{r = 1}^{n_{r+1}} \delta_r^{(k+1)} \cdot \frac{\partial z_r^{(k+1)}}{\partial z_j^{(k)}} \\ \end{split}\]
notiamo come abbiamo espresso l'error term della \(j\) esima unità del \(k\) esimo layer in funzione degli error term delle unità del successivo layer. Continuando,
\[\begin{split} \frac{\partial z_r^{(k+1)}}{\partial z_j^{(k)}} &= \frac{\partial z_r^{(k+1)}}{\partial a_j^{(k)}} \cdot \frac{\partial a_j^{(k)}}{\partial z_j^{(k)}} \\ &= w_{r, j}^{(k+1)} \cdot h^{'}_k(a_j^{(k)}) \\ \end{split}\]
troviamo quindi
\[\delta_j^{(k)} = h^{'}_k(a_j^{(k)}) \cdot \sum\limits_{r = 1}^{n_{r+1}} \delta_r^{(k+1)} \cdot w_{r, j}^{(k+1)}\]
e quindi il contributo del generico paramatro \(w_{j, l}^{(k)}\) che finisce in un hidden layer è dato da
\[\begin{split} \frac{\partial \mathcal{L}_i}{\partial w_{j, l}^{(k)}} &= \delta_r^{(k)} \cdot a_l^{(k-1)} \\ &= \Bigg(h^{'}_k(a_j^{(k)}) \cdot \sum\limits_{r = 1}^{n_{r+1}} \delta_r^{(k+1)} \cdot w_{r, j}^{(k+1)}\Bigg) \cdot a_l^{(k-1)} \\ \end{split}\]
Una volta che siamo in grado di calcolare il gradiente della funzione di costo rispetto ad ogni parametro, per effettuare il training del modello e calcolare il valore ottimale dei vari parametri è possibile utilizzare il noto algoritmo iterativo chiamato gradient descent.
La versione base dell'algoritmo funziona nel seguente modo:
Inizialmente si assegnano dei valori random ad ogni parametro della rete.
Successivamente si continuano ad aggiornare i parametri della rete nel seguente modo
\[w_{i,j}^{(l)} = w_{i,j}^{(l)} - \eta \cdot \frac{\partial J}{\partial w_{i,j}^{(l)}}\]
dove,
\(J\) è la funzione di costo rispetto a tutti gli elementi del training set.
\(\partial J/\partial w_{i,j}^{(l)}\) è il valore calcolato tramite la backpropagation e rappresenta la derivata parziale della funzione di costo calcolata rispetto al parametro \(w_{i,j}^{(l)}\).
\(\eta\) è il parametro noto come learning rate, e stabilisce la velocità di convergenza.
Il passo di update viene ripetuto fino a raggiungere un determinato criterio di convergenza, che può essere definito ad-hoc per lo specifico spazio dei parametri considerato. Ad esempio si potrebbe pensare di fermare l'algoritmo quando l'improvement ottenuto ad ogni iterazione rispetto alla funzione di costo diventa più basso di una pre-determinata threshold.
Per rendere più efficiente la discesa del gradiente ci sono poi delle variazioni dell'algoritmo, riportate a seguire:
Stochastic Gradient Descent: In questa versione al posto di calcolare la derivata dell'errore rispetto a tutti gli elementi del training set (ovvero di \(J\)), si considerata la derivata dell'errore di un singolo elemento del training set \(\mathcal{L}_h\). Così facendo la regola di update diventa
\[w_{i,j}^{(l)} = w_{i,j}^{(l)} - \eta \cdot \frac{\partial \mathcal{L}_h}{\partial w_{i,j}^{(l)}}\]
Batch Gradient Descent: Quest'altra versione invece considera l'errore rispetto ad un sottoinsieme del training set \(B\) di un size fissato \(b := |B|\). La regola di update diventa quindi
\[w_{i,j}^{(l)} = w_{i,j}^{(l)} - \eta \cdot \sum\limits_{x_h \in B} \frac{\partial \mathcal{L}_h}{\partial w_{i,j}^{(l)}}\]
Per rendere più efficiente e scalabile il processo di training di una rete neurale vengono presi i seguenti accorgimenti:
Caching: Notiamo come nelle equazioni ottenuta per la backpropagation appaiono molti termini della forma \(a_l^{(k-1)}, h^{'}_k(a_j^{(k)})\). Questi termini sono sempre calcolati durante il feedforward algorithm, ovvero quando la rete propaga in avanti l'esempio di training considerato in quel momento. L'idea è quindi quella di salvarsi in una cache i valori calcolati durante la fase di feedforward in modo tale da poterli riutilizzare successivamente per la fase di backward propagation.
Vectorization: Anche se teoricamente è possibile addestrare una rete neurale procedendo applicando il feedforward algorithm e poi il backward algorithm un esempio alla volta per poi procedere con la discesa del gradiente, da un punto di vista computazionale questo è molto costoso.
Per cercare di ottimizzare queste operazioni, e in particolare per cercare di sfruttare al massimo le capacità di parallelizzazione del calcolo delle schede grafiche (GPUs), si è introdotta la tecnica del broadcasting, che consiste nell'effettuare in contemporanea le operazione viste prima per il singolo training example.
In particolare è possibile definire una versione vettorizzata sia delle operazioni di feedforward, per propagare in avanti un insieme di esempi, e sia le operazioni di backward propagation, per calcolare il valore della derivata rispetto alla loss di più esempi.
Infine, per cercare di evitare problemi di overfitting, oltre ad aggiungere un termine di regolarizzazione esplicito nella funzione di costo, possiamo seguire le seguenti strategie:
Dropout: L'idea del dropout è quella di "spegnere", durante il processo di training, alcuni neuroni di un layer in modo randomico. Questa tecnica è stata introdotta nel 2014 da Svrivastav et al. e cerca di evitare che neuroni di layers diversi imparano le stesse cose
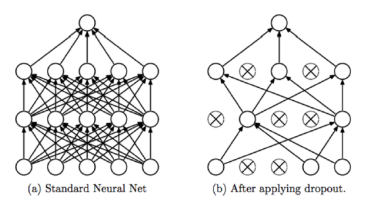
Early stopping: Un'altra tecnica è quella dell'early stopping, e consiste nel definire un criterio preciso in cui fermare il processo di training. In particolare nell'early stopping si divide il training set in due: l'effettivo training set e un validation set, si addestra il modello sul training set e si valuta l'errore del modello sul validation set. Non appena l'errore che il modello fa sul validation test aumenta, si ferma il processo e si fissano i pesi rispetto all'iterazione precedente.