Il Calcolatore Universale

L'importanza della Lettura

L'interesse per una materia come l'informatica può essere approfondito ed arricchito percorrendo tante strade diverse.

Tra tutte, la lettura è sicuramente una strada molto importante, anche nel mondo informatico.

Tra le altre cose, è stata proprio la lettura del libro

"Il Calcolatore Universale"

che mi ha esposto, per la prima volta, ad alcune delle idee più belle ed importanti della logica, della matematica, e dell'informatica.

Le conseguenze di questo incontro?

Mi sono innamorato dell'informatica.

Non a caso, ho portato come argomento della tesina delle superiori proprio la figura di Alan Turing, spezzata tra la teoria astratta della computabilità e la concreta pratica della crittografia.

Per chi fosse interessato: tesina superiori.

Ho dunque deciso di portare sul canale una serie di video in cui discuto brevemente alcuni dei libri più importanti del mio percorso.

Faccio questo con la speranza di poter far vivere a qualcun altro una sensazione simile a quella vissuta da me stesso anni fa.

Cominciamo quindi con il primo vero libro che ho letto che parlava di informatica…

Il Calcolatore Universale

Microprocessor (CRISP), 172.000 transistors, AT&T Bell Laboratories (1986)

La pecularità di questo libro è che non parla solamente dei lati tecnici di materie quali la logica, la matematica e l'informatica.

Questo libro parla anche di gioie, di felicità, di sofferenze, di malattie, di frustrazioni e di ideali.

Ebbène sì: le vite dei logici, dei matematici e degli informatici possono essere alquanto caotiche, emotive e motivate da potenti ideali, sia nella gioia che nel dolore.

In altre parole, questo libro parla di esseri umani che svolgono una attività umana:

ragionare attraverso la logica e l'intuizione

Sinossi

Tra i fili di Arianna che si possono seguire per interpretare lo sviluppo del moderno, Martin Davis seleziona quell'entità al tempo stesso astrusa e comunissima che è il calcolo o computazione.

Astrusa perché la teoria della calcolabilità – in bilico tra matematica, ingegneria elettronica e filosofia – non è certo un soggetto facile.

Comunissima perché chiunque usi un PC ha tra le mani, spesso senza saperlo, un "calcolatore universale" – l'epitome stessa della nozione di computazione.

Per ricostruire la genesi di questa idea Davis prende le mosse da Leibniz e compone, con affetto e rispetto, una galleria di personaggi-chiave che comprende Boole, Frege, Cantor, Hilbert, Gödel e culmina in Turing: alla sua macchina universale riconosce infatti, pur pagando il dovuto tributo a Gödel, un ruolo centrale nei fenomeni di insolubilità.

Grazie a Turing il "sogno di Leibniz" – l'invenzione di un calcolo simbolico con cui risolvere in maniera automatica ogni genere di problemi – si materializza in calcolatori non più in carne e ossa, ma in rame e silicio.

Resta tuttavia, quel sogno, solo in parte realizzato: se molti degli aspetti della mente razionale sono oggi riproducibili informaticamente, quelli che più caratterizzano l'essere umano – senso comune, emozioni, coscienza – resistono ancora alla realizzazione della visione di Leibniz.

Logici, Matematici, Informatici e Ingegneri

Come si evince dalla sinossi, questo libro parla di tante persone, e in particolare parla dei principali matematici e logici che nel corso degli anni hanno posto le basi a quella che poi è diventata l'informatica teorica.

Tra questi nomi troviamo:

\[\begin{split} &\text{Leibniz} \;\;&\;\; \text{(1646, 1716)} \\ &\text{Bool} \;\;&\;\; \text{(1815, 1864)} \\ &\text{Frege} \;\;&\;\; \text{(1848, 1925)} \\ &\text{Cantor} \;\;&\;\; \text{(1845, 1918)} \\ &\text{Hilbert} \;\;&\;\; \text{(1862, 1943)} \\ &\text{Gödel} \;\;&\;\; \text{(1906, 1978)} \\ &\text{Turing} \;\;&\;\; \text{(1912, 1954)} \\ &\text{John von Neumann} \;\;&\;\; \text{(1903, 1957)} \\ \end{split}\]

Il risultato combinato di queste persone nel corso degli anni è stata anche la macchina di Turing, uno dei più semplici modelli matematici che riesce a catturare in modo intuitivo il concetto di calcolo.

Per chi fosse interessato ad approfondire che cos'è esattamente una macchina di Turing, rimando al video che ho già fatto sul canale:

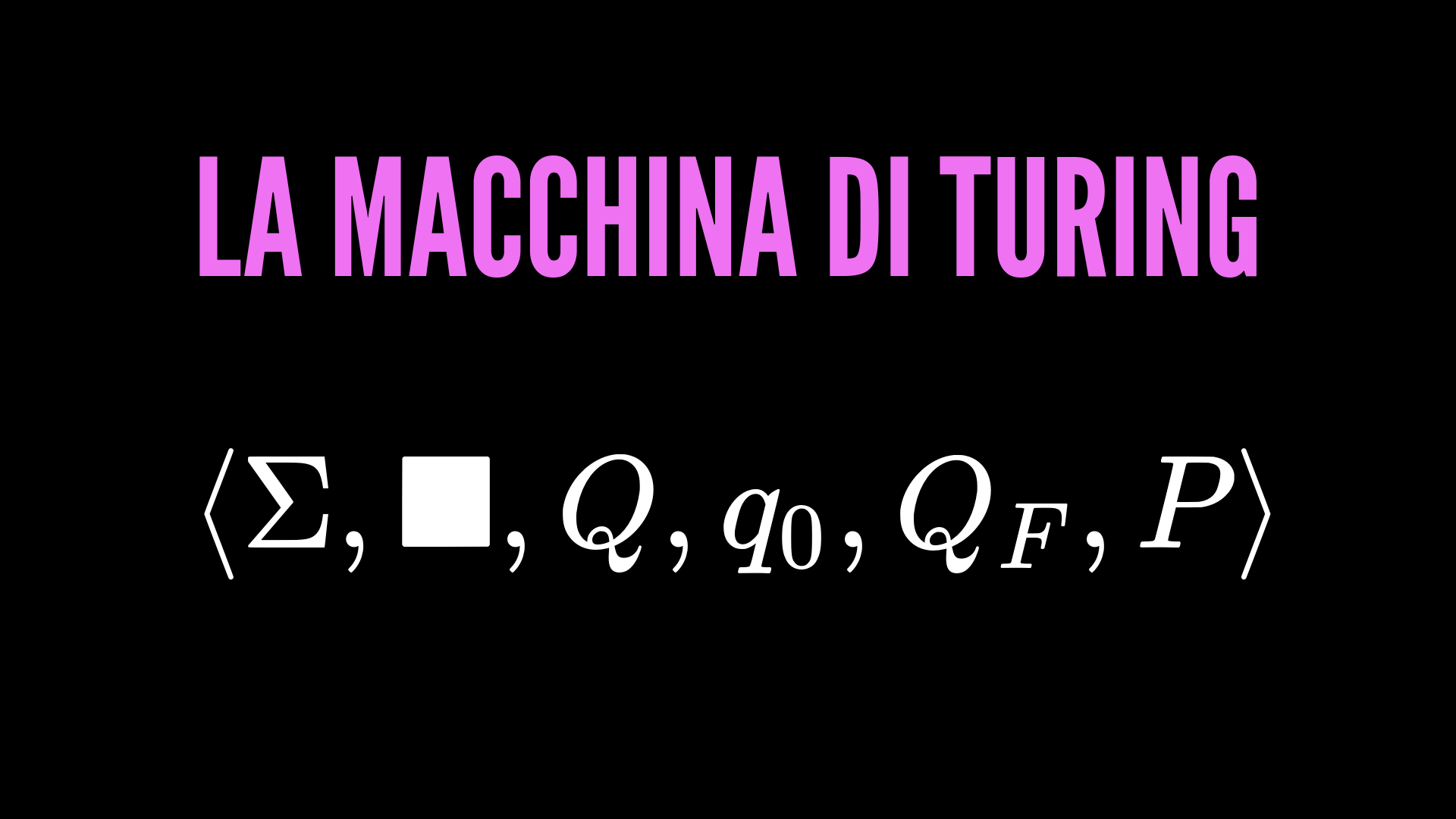
Link: La Macchina di Turing

Dalla teoria si è poi passata alla pratica, con la costruzione dei primi calcolatori in "carne ed ossa".

Tra questi troviamo anche:

• COLOSSUS.
• ENIAC (Electronic Numerical Integrator And Computer).
• EDVAC (Electronic Discrete Variable Automatic Computer).
• ACE (Automatic Computing Engine).

L'EDVAC (Electronic Discrete Variable Automatic Computer), costruito come successore di ENIAC alla Moore School of Electrical Engineering, in Pensylvania.

L'ACE (Automatic Computing Engine), progettato direttamente da Alan Turing.

Col passare del tempo questi dispositivi sono diventati sempre più piccoli e potenti.

Talmente piccoli da finire dentro le nostre tasche.

link

Quanto bella può essere un'idea?

L'impatto principale che la lettura del libro ha avuto sulla mia vita è stato proprio l'incontro, per la prima volta, con una serie di idee nuove ed affascinanti.

Inoltre, dopo la prima lettura non avevo capito nessuna di queste idee fino in fondo.

Anzi, non le avevo nemmeno capite superficialmente.

Eppure le ho trovate talmente tanto interessanti che ho deciso di continuare ad impegnarmi per capirle meglio.

In altre parole, è stata la prima volta in cui non ho potuto tollerare la mia ignoranza.

Ho sentito sulla mia pelle una banale realtà:

che per capire la bellezza di certe cose è necessario impegnarsi con criterio

Mi sono quindi iscritto all'università con un obiettivo:

approfondire queste idee in modo da capirle appieno

Tra queste idee troviamo anche le seguenti:

• Il sogno di Leibniz
• L'algebra booleana di Boole
• L'ideografia di Frege
• Gli insiemi di Cantor
• I principia mathematica di Russel e Whitehead
• Il programma di Hilbert
• I teoremi di incompletezza di Gödel
• La macchina di Turing
• Il computer digitale