ADRC - 09 - Modello Probabilistico
1 Lecture Info
Data:
Nel mondo moderno dell'informatica i modelli puramente deterministici non sono molto potenti. Se si è interessati a modellare reti complesse reali necessitiamo di introdurre ed analizzare processi distribuiti di natura probabilistica. In questa lezione quindi introduciamo un modello probabilistico distribuito, e facciamo vedere come risolvere il problema della leader election-- trattato nella sua versione deterministica la lezione precedente--in modo probabilistico.
2 Modello Probabilistico Distribuito
Il modello che abbiamo in mente è essenzialmente il modello deterministico già descritto, con l'aggiunta però che ogni nodo \(v \in V\) della rete può accedere ad una sorgente privata di random bits denotata con \(S(v)\). Si indica con \(r\) il massimo numero di random bits che ogni nodo può utilizzare.
Se \(u\) e \(v\) sono nodi diversi, \(u \neq v\), allora le v.a. \(S(u)\) e \(S(v)\) sono indipendenti tra loro, e quindi
\[Pr[S(u) = 1, \,\,\, S(v) = 0] = Pr[S(u) = 1] \cdot Pr[S(v) = 0]\]
Lo spazio di probabilità generato da un protocollo probabilistico che lavora su un grafo \(G=(V,E)\) è descritto come segue
\[\Omega\Big(\{0, 1\}^{n \cdot r}, \,\,\, \forall\,\,\, \overline{y} \in \{0, 1\}^{n \cdot r}: \,\, Pr(\overline{y}) = \frac{1}{2^{n \cdot r}}\Big)\]
dove l'insieme dei possibili eventi è l'insieme delle sequenze di \(n \cdot r\) bits, e le varie sequenze hanno la stessa probabilità uniforme di verificarsi. Da notare poi che fissata una specifica sequenza $\overline{y} \{0, 1\}$ il protocollo diventa deterministico.
Osservazione: Dato che lavoriamo sempre con spazi di probabilità finita, per calcolare la probabilità di errore di un protocollo distribuito ci basta contare il numero di sequenze di random bits \(\overline{y} \in \{0, 1\}^{n \cdot r}\) che portano ad uno stato di errore.
3 Leader Election Randomizzata
Supponiamo di conoscere il numero di nodi \(n\) della nostra rete, e supponiamo di lavorare con reti che hanno una topologia ad anello
Andiamo adesso a descrivere un protocollo probabilistico per eleggere un leader. Il protocollo è diviso in due fasi, che sono:
Fase I: Ogni nodo initiator \(v \in V\) che si sveglia sceglie un valore \(j_v\) in modo uniforme dall'insieme \(\{1, ..., m\}\) e manda un messaggio di wake-up ai suoi vicini, che ripetono la stessa procedura.
Ogni nodo \(v \in V\) può simulare la scelta dell'etichetta andandosi a generare \(\lfloor \log_2 n \rfloor\) random bits in modo uniforme.
Fase II: Una volta che tutti i nodi hanno generato una loro etichetta, si esegue uno degli algoritmi per la leader election deterministica visti nella precedente lezione.
Osservazione Per denotare la scelta in modo uniforme di \(j_v\) dall'insieme \(\{1, ..., m\}\) si può utilizzare la seguente notazione
\[j_v \in_U \{1, ..., m\} \iff \forall j \in \{1, ..., m\}: \,\, Pr[j_v = j] = \frac{1}{m}\]
3.1 Analisi Correttezza
Iniziamo notando che, se dopo aver generato tutte le etichette, tutti i nodi hanno etichette tra loro distinte, allora la fase II termina sempre in modo corretto.
Ai fini dell'analisi definiamo i seguenti eventi
\[\begin{split} \text{ERROR} &:= \text{ il protocollo fallisce } \\ \text{BAD} &:= \exists v, w \in V: \,\,\, v \neq w \implies j_v = j_w \\ \end{split}\]
questi eventi sono relazionati tra loro nel seguente modo
\[\text{ERROR } \implies \text{ BAD } \,\,\,\, (\text{o ERROR } \subseteq \text{ BAD})\]
infatti l'unico caso in cui il protocollo fallisce è quando le etichette vengono generate con almeno un doppione. In termine di probabilità troviamo quindi
\[Pr[\text{ERROR}] \leq Pr[\text{BAD}]\]
Continuando, per analizzare l'evento \(\text{BAD}\) possiamo utilizzare un processo tipicamente chiamato balls-into-bins. L'idea è quella di mappare ogni esecuzione del protocollo ad una particolare associazione tra balls e bins
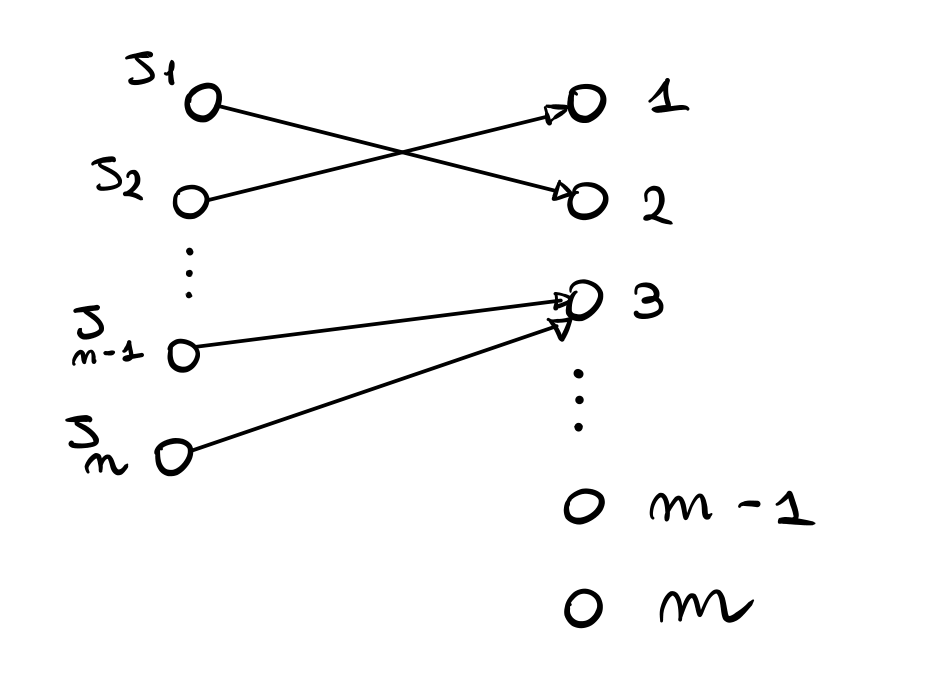
Nel nostro caso le balls sono le etichette, mentre i bins sono i valori che le etichette possono assumere. Utilizzando questa modelizzazione l'evento \(\text{BAD}\) succede se e solo se \(2\) o più balls vanno nello stesso bin. Al fine di calcolare la probabilità di tale evento iniziamo calcolando la probabilità che \(k\) etichette, con \(k \geq 2\), finiscono nel bin \(i\), che è la seguente
\[\binom{n}{k} \cdot \Big(\frac{1}{m}\Big)^k \cdot \Big(1 - \frac{1}{m}\Big)^{n - k}\]
Sommando tale espressione al variare di \(k\) per \(k \geq 2\) otteniamo la probabilità dell'evento \(\text{BAD}_i\), intenso come l'evento in cui il bin \(i\) porta al fallimento del protocollo. Tale probabilità può essere limitata nel seguente modo
\[\begin{split} Pr[\text{BAD}_i] &= \sum_{k = 2}^n \binom{n}{k} \cdot \Big(\frac{1}{m}\Big)^k \cdot \Big(1 - \frac{1}{m}\Big)^{n - k} \\ &\leq \sum_{k = 2}^n \binom{n}{k} \Big(\frac{1}{m}\Big)^k \\ &\leq \sum_{k = 2}^n \Big(\frac{e \cdot n}{k}\Big)\cdot \Big(\frac{1}{m}\Big)^k \,\,\,\,\, \text{(stirling)}\\ &= \Big(\frac{e \cdot n}{2 \cdot m} \Big)^2 + \sum_{k = 3}^n \Big(\frac{e \cdot n}{k \cdot m} \Big)^k \\ &\leq \Big(\frac{e \cdot n}{2 \cdot m} \Big)^2 + n \cdot \Big(\frac{e \cdot n}{3 \cdot m} \Big)^3 \\ &= O\Big(\frac{n^2}{m^2} + \frac{n^4}{m^3}\Big) \\ \end{split}\]
Dato che l'errore può avvenire in qualsiasi bin, abbiamo che l'evento \(\text{BAD}\) è ottenuto dall'unione degli eventi \(\text{BAD}_i\), al variare di \(i \in \{1, ..., m\}\). Troviamo quindi
\[Pr[\text{ERROR}] \leq Pr[\text{BAD}] = Pr\Big[ \bigcup_{i = 1}^m \,\, \text{BAD}_i\Big]\]
Notiamo che gli eventi \(\text{BAD}_i\) non sono indipendenti tra loro. Per calcolare la probabilità della loro unione bisogna quindi utilizzare degli strumenti probabilistici appositi. Il più semplice tra questi strumenti è chiamato union bound, e ci dice che se \(A_1, ..., A_k\) sono eventi, allora
\[Pr\Big[ \bigcup_{i = 1}^k A_i \Big] \leq \sum\limits_{i = 1}^k Pr[A_i]\]
Nel nostro caso in particolare abbiamo
\[\begin{split} Pr[\text{ERROR}] \leq Pr[\bigcup_{i = 1}^m \text{BAD}_i] &\leq \sum\limits_{i = 1}^m Pr[\text{BAD}_i] \\ &\leq m \cdot Pr[\text{BAD}_1] \\ &\leq m \cdot O\Big(\frac{n^2}{m^2} + \frac{n^4}{m^3}\Big) \\ &= O\Big( \frac{n^2}{m} + \frac{n^4}{m^2} \Big) \\ \end{split}\]
Per far funzionare il protocollo con alta probabilità dunque ci basta scegliere \(m \geq n^3\). Con questa scelta infatti otteniamo
\[Pr[\text{ERROR}] \leq O\Big(\frac{1}{n} + \frac{1}{n^2}\Big) = O\Big(\frac{1}{n}\Big)\]
3.2 Random Bits Utilizzati
Nei sistemi distribuiti i random bits sono molto difficili da generare. Questo rende il numero di random bits una misura di complessità molto importante da analizzare.
Nel caso del protocollo appena analizzato, ciascun nodo utilizza
\[\log_2 m = \log_2 n^3 \leq 4 \log n\]
random bits, il che è una quantità ragionevole.
4 Concentrazione di Variabili Aleatorie
Molte volte data una variabile aleatoria non siamo interessati solo a fare una analisi in media, ovvero a calcolare il valore atteso della v.a., ma vogliamo anche capire quanto i valori assunti dalla v.a. sono concentrati intorno al valore medio.
Per fare un esempio, supponiamo di considerare i lanci di una moneta bilanciata. Indichiamo con \(X\) la v.a. che conta il numero di teste ottenuta da \(n\) lanci indipendenti. Abbiamo che,
\[Pr[X = k] = \binom{n}{k} \cdot \Big(\frac{1}{2}\Big)^k \cdot \Big(\frac{1}{2}\Big)^{n-k} = \binom{n}{k} \cdot \Big(\frac{1}{2}\Big)^n\]
Il valore medio di \(X\) è dato da
\[\mathbb{E}[X] = \sum_{k = 0}^n k \cdot Pr[X = k] = \frac{n}{2}\]
Approssimando, la forma della distribuzione di \(X\) ha la seguente forma
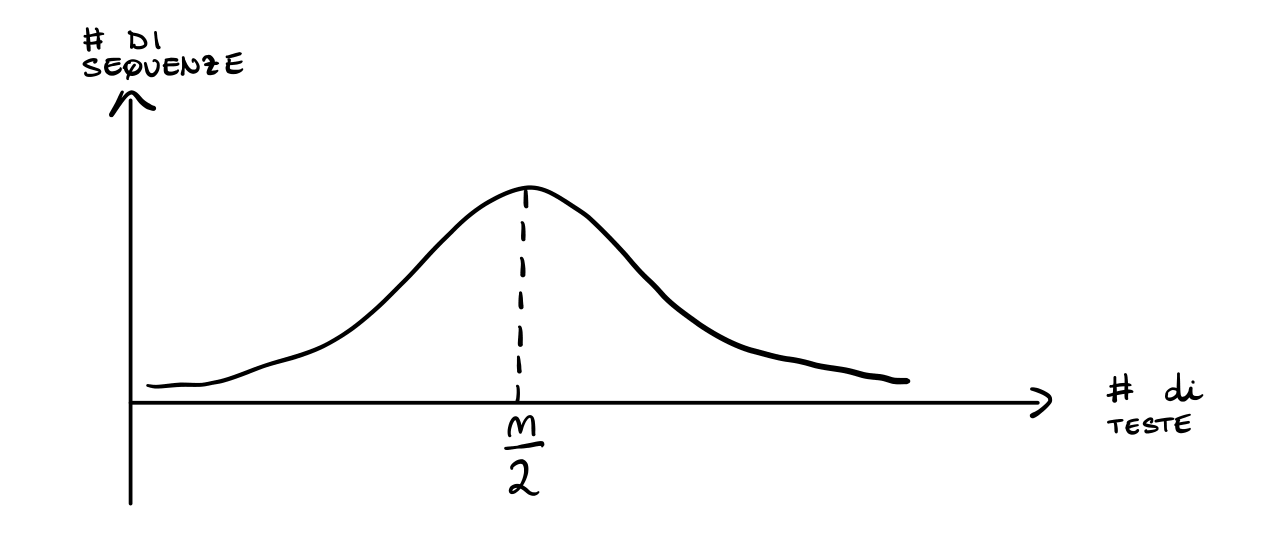
Siamo quindi interessati a capire quanto la distribuzione è concentrata vicino al valor medio. In particolare quindi vogliamo capire con che velocità descresce la probabità di assumere un particolare valore, all'aumentare della distanza di quel valore dalla media.
Per certe distribuzioni, come ad esempio la distribuzione binomiale riportata sopra, è possibile dimostrare che c'è una concentrazione esponenziale intorno al valore medio, il che significa dire che più ci si allontana dal valore medio e più la probabilità che la v.a. assume valori a quella distanza dal valore medio decresce in modo esponenziale.
Per dimostare risultati di concentrazione si possono utilizzare vari strumenti probabilistici, tra cui troviamo i seguenti.
4.1 Markov Inequality
La Markov inequality non ci permette di ottenere una decrescita esponenziale, ma può essere utilizzata per ogni v.a. a valori positivi.
Essa ci dice che, per ogni v.a. \(X \geq 0\), posto \(\mu = \mathbb{E}[X]\), vale
\[\forall t: \,\,\, Pr[X \geq t] \leq \frac{\mu}{t}\]
4.2 Chernoff Bounds
I chernoff bounds possono invece essere utilizzati per ottenere degli intervalli di concentrazione con alta probabilità. Ci sono varie versioni dei chernoff bounds. A seguire ne riportiamo una in particolare.
Siano \(X_1, ..., X_n\) delle v.a. binarie mutualmente indipendenti, e definiamo
\[X := \sum_{i = 1}^n X_i \,\,\,\,,\,\,\,\, u := \mathbb{E}[X]\]
allora per ogni \(delta\) tale che \(0 < \delta < 1\), vale
\[Pr[X \geq (1 + \delta) \cdot \mu] \leq e^{\displaystyle{-\frac{\delta^2}{3} \cdot \mu}}\]
4.2.1 Esempio
Nel caso dei lanci delle monete, abbiamo che
\[Pr[ X \geq \Big(1 + \frac{2}{3} \Big) \cdot \frac{n}{2} ] \leq e^{\displaystyle{\frac{-\frac49 \cdot \frac{n}{2} }{3}}} = e^{\displaystyle{-\frac{2}{27} \cdot n}}\]
Quindi la probabilità che \(X\) di discosti di una frazione costante dal valore medio decresce in modo esponenziale al crescere di \(n\). In particolare, se si sceglie \(\delta := c \cdot \sqrt{\frac{\log n}{n}}\), si ottiene una probabilità di
\[\leq Exp\Big( -c \frac{\log n}{3n} \cdot \frac{n}{2} \Big) = Exp\Big(-\frac{c}{6} \cdot \log n\Big) = \displaystyle{\frac{1}{n^{\frac{c}{6}}}}\]